Урок на тему "Прості і складені числа "
Мета: Навчити учнів розрізняти прості і складені числа; застосовувати основні теореми про прості числа; вдосконалювати навички розв'язування задач на подільність чисел.
РОзробка уроку також містить презентацію «Прості та складені числа»Цикл уроків з алгебри на тему «Основи теорії подільності»
для 8 класів з поглибленим вивченням математики
підготувала вчитель математики
НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів - гімназія
Дем´янюк Ганна Володимирівна
Урок №8
Тема: Прості і складені числа
Мета: Навчити учнів розрізняти прості і складені числа; застосовувати основні теореми про прості числа; вдосконалювати навички розв’язування задач на подільність чисел.
Тип уроку: комбінований урок
Обладнання: підручник, презентація «Прості та складені числа», картки
Хід уроку:
1. Мотивація вивчення теми «Прості та складені числа»
- Захист творчої роботи «Історія простих чисел. Числа-близнюки»
- Повідомлення на тему «Решето Ератосфена»
- Пояснення нового матеріалу
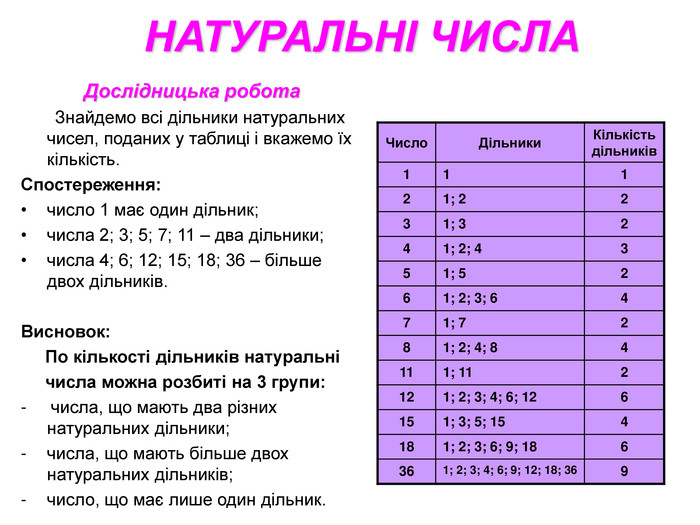
Візьмемо кілька натуральних чисел і знайдемо усі їхні дільники.
|
Числа |
Дільники |
Кількість дільників |
|
1 2 3 4 12 17 21 30 |
1 1, 2 1, 3 1, 2, 4 1, 2, 3, 4, 6, 2 1, 17 1, 3, 7, 21 1, 2, 3, 5, 6, 10, 5, 30 |
1 2 2 3 6 2 4 8 |
Бачимо, що числа мають різну кількість дільників.
Число 1 має найменше дільників — лише один. Числа 2, З, 17 мають по два дільники: 1 і самого себе. Числа 4, 12, 21 і 30 мають більше, ніж два дільники.
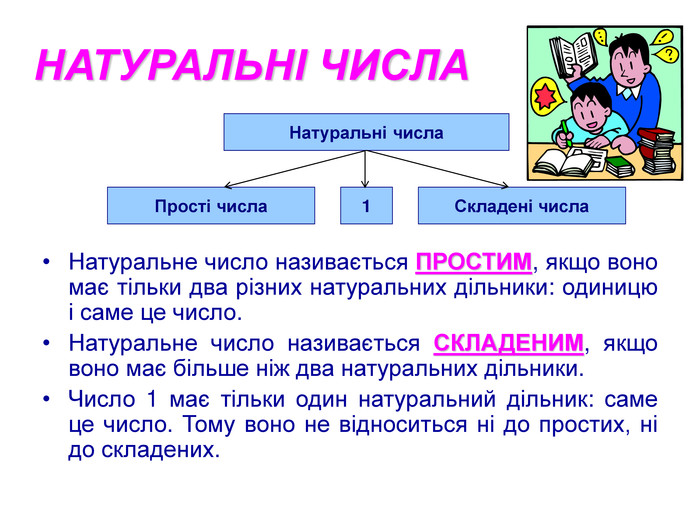
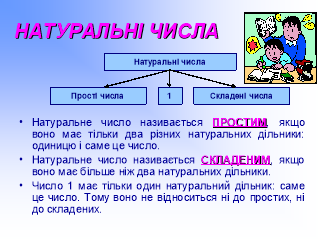
Означення: Натуральне число називають простим, якщо воно має тільки два різні дільники: одиницю і саме це число.
Означення: Натуральне число, яке мас більше, ніж два дільники, називають складеним.
Отже, числа 2, 3, 17 — прості, а числа 4, 12, 21, 30 — складені. Число 1 не належить ні до простих, ні до складених.
- Якщо число має дільник, відмінний від 1 і самого себе, то це число має більше, ніж два дільники, і тому воно є складеним. Число 12 475 — складене, бо має дільником,наприклад, число 5.
- Найменшим простим числом є число 2. Найбільшого простого числа не існує. Усі прості числа, крім числа 2, є непарними.
Презентація «Прості числа»
Теорема: Множина простих чисел є нескінченною
- Розв’язування вправ
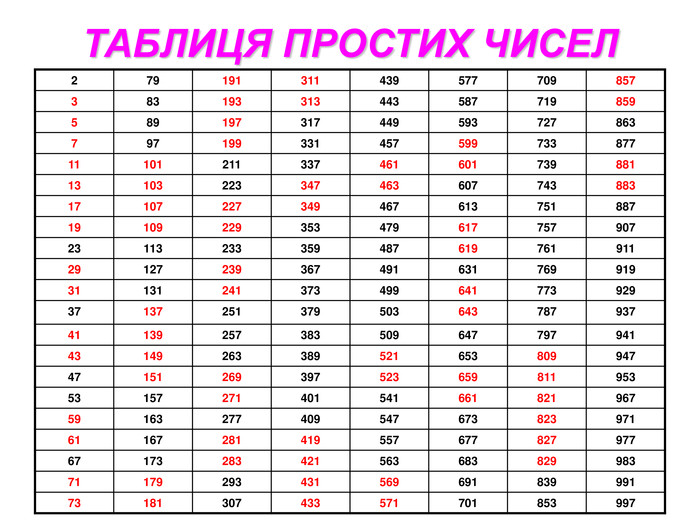
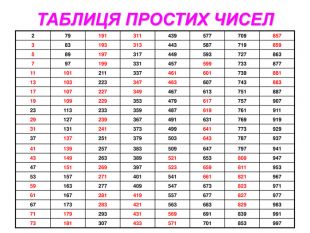
- Усно (робота з таблицею простих чисел)
- Назвіть перші десять простих чисел.
- Назвіть саме найменше просте число? Парним чи непарним є це число? Знайдіть ще парні прості числа. Зробіть висновки.
- Чи є числа 87; 47 простими?
- Назвіть всі прості числа, які більші за 40, але менші за 50.
- Яке просте число слідує за числом 14?
- Знайдіть пари простих чисел, різниця між якими дорівнює 2.
- Знайдіть трійки простих чисел такі, щоб різниця між кожним наступним і попереднім дорівнювала 2.
8. Чи правильне твердження: а) кожне парне число є складеним;
б) добуток двох простих чисел є складеним числом?
- Письмово (робота в групах, завдання на картках )
1) Доведіть, що числа 175 410, 368 136, 195 435, 111 111, 909 909 є складеними.
2) Чи є значення виразів 112 + 3148, 103 • 11 та 14 + 3 складеними числами?
3)Скільки дільників мають числа? Випишіть спочатку прості числа, а поти складені: а) 26; 41; 63; 72; 82; 91; б) 14; 33; 37; 40; 43; 65.
4)Запишіть замість зірочки таку цифру, щоб утворилося складене число:
а) 317*; 6)1*23; в) 51*77, г) 7*41; д)418*;е) 18*96.
5) Чи можна записати просте трицифрове число, використавши лише один раз кожну із цифр: а) 2, 6, 8; 6)0,0,7; в) 1,2, З?
6). Щоб перевірити, буде число 323 простим чи складеним, Миколка почав послідовно перевіряти, чи будуть числа 2, 3, 4, 5, 6, ... дільниками числа 323. Однак встановивши, що число 3 не є дільником числа 323, Миколка відразу міг би сказати, що деякі наступні числа також не є дільниками числа 323. Які це числа?
7) Число n просте, до того ж, n > 2. Чи буде наступне за ним число n + 1 простим?
8) Перемноживши чотири простих послідовних числа, Наталя одержала в результаті число, остання цифра якого дорівнює нулю. Які числа вона перемножила і який результат одержала?
9) Знайдіть усі натуральні n, при яких є простим числом значення виразу:
А) n3-1; Б) 3n2 +4n-15; В) 8n-1
10) Прості числа p та q такі, що p>3 та q <3. Доведіть, що ![]() .
.
4. Домашня робота
1. Знайдіть усі натуральні n, при яких є простим числом значення виразу:
А) n+-1; Б) 4n2 +5n-21; В) 3n-1
2. Доведіть, що коли число p просте і p>3 , то ![]() .
.
Використані джерела:
1. Алгебра підручник для 8 класу з поглибленим вивченням математики,
А.Г. Мерзляк, В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009
2. Алгебра та початки аналізу 10 клас, профільний рівень
А.Г. Мерзляк, Д.А. Номіровський, В.Б. Полонський, М.С. Якір, - Харків «Гімназія», - 2010
3. О.Ю. Карік, Матеріали для факультативних занять, спецкурсів, гуртків, математика 5-7, Харків, - «Основа», - 2008
Презентація 1














про публікацію авторської розробки
Додати розробку