Урок на тему: "Ознаки подільності"

Цикл уроків з алгебри на тему «Основи теорії подільності»

для 8 класів з поглибленим вивченням математики 

                підготувала вчитель математики

 НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів  - гімназія

 Дем´янюк Ганна Володимирівна

Урок №7

Тема: Ознаки подільності

Мета: Навчити учнів трактувати ознаки подільності натуральних чисел у загальному вигляді за допомогою «мови конгруенції»; розвивати навички та вміння розв’язувати завдання на подільність; виховувати організованість, мотиви діяльності.

Тип уроку: комбінований урок

Обладнання: підручник, картки

Хід уроку:

1. Актуалізація знань

  (фронтальне опитування)

• які ознаки подільності вам відомі з попередніх класів?
• як можна узагальнити ознаку подільності на 2, 4, 8,16…?
• навіщо вивчати ознаки подільності?

2. Пояснення нового матеріалу.

 Узагальнимо ознаки подільності на 2,5,10,3 і 9 за допомогою «мови конгруенції»

Теорема:

Доведення: Запишемо очевидні конгруенції:

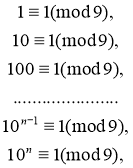
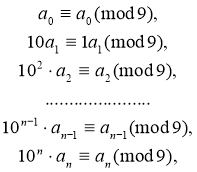  Помножимо обидві частини першої             конгруенції на

, другої – на , третьої – на ….. -ї – на . Маємо

Додавши ці конгруенції, отримаємо:

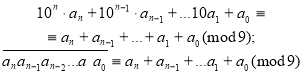
Наслідок (ознака подільності на 9) Натуральне число ділиться націло на 9 тоді й тільки тоді, коли сума цифр його десяткового запису ділиться націло на 9.

Теорема:

Наслідок (ознака подільності на 3) Натуральне число ділиться націло на 3 тоді й тільки тоді, коли сума цифр його десяткового запису ділиться націло на 3.

Теорема:

Наслідок (ознака подільності на 11). Пронумеруємо цифри десяткового запису натурального числа справа наліво числами 0,1,2,…, n. Натуральне число ділиться націло на 11 тоді і тільки тоді. Коли різниця між сумою цифр з парними номерами і сумою цифр з непарними номерами ділиться націло на 11.

Наприклад, для числа 2387605 маємо: (5+6+8+2)-(0+7+3)=11. Отже, це число кратне 11.

1) Доведіть, що число 1000003000001 не є квадратом натурального числа.

Розв’язання. Сума цифр даного числа дорівнює 5. Отже, це число при діленні на 3 дає остачу 2. Проте квадрат натурального числа при діленні на3 дає в остачі або 0, або 1.

3. Розв’язування вправ

• Робота біля дошки

1) Доведіть, що

2) Доведіть, що

 - робота в групах (завдання на картках)

1. Запишіть, використовуючи по одному разу кожну з цифр 0, 1, 4, 7, найбільше і найменше чотирицифрові числа, які кратні 15.

2. До числа 15 допишіть зліва і справа по одній цифрі так, щоб утворене число було кратне 15. Скільки розв’язків має задача?

3. Замість зірочок поставте такі цифри, щоб число 3*4* ділилося націло на 9. Знайдіть усі можливі розв’язки.

4. Замість зірочок поставте такі цифри, щоб число 42*4* ділилося націло на 72.

5. Знайдіть найменше натуральне число, кратне 36, у запису якого зустрічаються всі 10 цифр.

6. Чи існує натуральне число, добуток цифр якого дорівнює 143341143?

7. Чи може натуральне число. У записі якого є тільки цифри 0 і 6,бути квадратом натурального числа?

8. Розв’яжіть рівняння: .

4) Домашня робота

1) Доведіть, що

2) До числа 34 допишіть зліва і справа по одній цифрі так, щоб утворене число було кратне 5. Скільки розв’язків має задача?

3) Замість зірочок поставте такі цифри, щоб число *74* ділилося націло на 18. Знайдіть усі можливі розв’язки.

4) Замість зірочок поставте такі цифри, щоб число 283*64* ділилося націло на 55.

Використані джерела:

1. Алгебра підручник для 8 класу з поглибленим вивченням математики,

А.Г. Мерзляк,  В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009

2. Алгебра та початки аналізу 10 клас, профільний рівень

А.Г. Мерзляк, Д.А. Номіровський,  В.Б. Полонський, М.С. Якір, - Харків «Гімназія», - 2010

3. О.Ю. Карік, Матеріали для факультативних занять, спецкурсів, гуртків, математика 5-7, Харків, - «Основа», -  2008