Урок на тему "Формула Герона. Формули радіусів вписаного й описаного кіл трикутника".

Геометрія,    9 клас.

Тема уроку. Формула Герона .Формули радіусів вписаного й описаного кіл    трикутника.

Мета уроку: формування предметних компетентностей:

                       удосконалити вміння обчислювати площу трикутника, зокрема за формулою Герона, за радіусом кола, описаного навколо трикутника, та радіусом кола, вписаного в трикутник;

                       формування ключових компетентностей:

                       формувати  вміння ставити запитання і розпізнавати проблему;

                       формувати здатність застосовувати навички роботи в парі;

                       сприяти вихованню чесності, відповідальності за свої дії;

Тип уроку: комбінований.

Наочність і обладнання: мультимедійна дошка

Вимоги до рівня підготовки учнів: використовують формулу Герона під час розв'язування задач.

Хід уроку

1.Організаційний момент.

2. Перевірка домашнього завдання

Перевірити наявність виконаних домашніх завдань та відпо­вісти на запитання, які виникли в учнів при їх виконанні.

Математичний диктант

1. Знайдіть площу прямокутника зі сторонами 2 см і 3 см.
2. Знайдіть площу прямокутного трикутника з катетами 3 см і 2 см.
3. Знайдіть площу правильного трикутника зі стороною 2 см.
4. Знайдіть площу паралелограма зі сторонами 2 см і 4 см, якщо кут між сторонами становить 30°.
5. Знайдіть площу ромба, діагоналі якого дорівнюють 3 см і 4 см.
6. Знайдіть площу трикутника, сторони якого дорівнюють 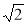см і 3 см, а кут між ними становить 135°.( sin 135° = sin45°)

)Відповіді. 1) 6 см²; 2) 3 см²; 3) см²; 4) 4 см²; 5) 6 см²; 6) 1,5 см².

3. Сприймання й усвідомлення нового матеріалу

Сьогодні ми ознайомимося з тим, як можна знайти площу трикутника, якщо відомі три його сторони. Цю формулу одержав Герон Александрійський, давньогрецький учений, який жив в Александрії в І ст. н. є. Відомо, що він був ученим-інженером, займався геодезією і прикладною математикою.

Формулу виводять на дошці учні, які готовилися до даного етапу уроку заздалегіть.

Розв'язування задач (робота в парах)

1.Знайдіть площу трикутника за трьома сторонами  

а) 17, 65, 80;       б) , , 6;     Відповідіа)  288 ; б) 10.

2.№ 5.13

4.  Закріплення й осмислення нового матеріалу

 Колективне розв'язування задач

Сторони трикутника дорівнюють а, b, с. Знайдіть висоту трикутника, опущену на сторону с.

Розв'язання

,  .

Оскільки S = ch_c, то h_c = = .

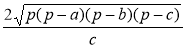Відповідь. .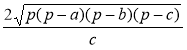

Самостійне розв'язування задач (один з учнів працює на закритій дошці)

Сторони трикутника дорівнюють 30 см , 25 см і 25 см. Знайдіть висоту трикутника, опущену на сторону 25 см.

Розв'язання

 ,

(см²).

S = ∙ 25 ∙ h, 300 = ∙ 25 h, h = = 24 (см).

Відповідь. 24 см.

IV. Самостійна робота

Варіант 1

1. Знайдіть найменшу висоту трикутника зі сторонами 5, 5, 6.

Варіант 2

1. Знайдіть найменшу висоту трикутника зі сторонами 17, 65, 80.

Розв'язання до завдань самостійної роботи

Варіант 1

1. = 8, = 12(см²).

S = ∙ 6 h, h = - = = = 4 (см).

Відповідь. 4 см.

Варіант 2

1. = 81, = 288(см²).

S = ∙ 80 ∙ h, h = = = 7,2 (см).

Відповідь. 7,2 см.

V. Домашнє завдання

Розв'язати задачі: № 5.8; 5.14.

VI.  Підбиття підсумків уроку Завдання класу

1. Запишіть відомі вам формули для знаходження площі три­кутника.
2. Знайдіть площу трикутника, якщо його сторони дорівню­ють 3 см, 3 см і  2 см.