Урок на тему "Корені многочлена. Теорема Безу."

Цикл уроків з алгебри на тему «Основи теорії подільності»

для 8 класів з поглибленим вивченням математики 

                підготувала вчитель математики

 НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів  - гімназія

 Дем´янюк Ганна Володимирівна

Урок №13

Тема: Корені многочлена. Теорема Безу.

Мета: навчити учнів знаходити корені многочлена; застосовувати теорему Безу для визначення остач від ділення многочленів на лінійні двочлени

Тип уроку: засвоєння нових знань

Обладнання: підручник, презентація 1, презентація 2

Хід уроку:

1. Мотивація уроку

 Проблемне питання:

- А чи можна визначити остачу при діленні многочленів, не застосовуючи метод «кута»?

Творче завдання:

Повідомлення про французького математика  Етьєна Безу (Презентація 1)

2. Пояснення нового матеріалу

Презентація 2

• Означення: Число α називають коренем многочлена А(х), якщо А(α)=0

Зрозуміло, що корінь многочлена А(х) – це корінь рівняння А(х)=0.

Множину коренів рівняння знайти не важко. Але якщо це рівняння записати у такому вигляді , то пошук його коренів викликатиме певні труднощі.

• Тому при розв´язуванні рівнянь виду А(х)=0, де А(х) - многочлен, важливо навчитися виділяти в многочлені лінійний множник, тобто подавати многочлен у вигляді добутку: А(х)=(х-α)В(х),  де В(х) - деякий многочлен, степінь якого на 1 менший від степеня многочлена А(х).
• Теорема (Безу): Остача від ділення многочлена А(х) на двочлен х-α дорівнює А(α).

Доведення: Оскільки степінь дільника (двочлена ) дорівнює 1, то степінь остачі має дорівнювати нулю або остача має бути нульовим многочленом, тобто шукана остача – це деяке число r. Для якого маємо: . Підставивши в цій рівності , отримаємо . Звідси .

• Теорема: Для того щоб число α було коренем многочлена А(х), необхідно й достатньо, щоб многочлен А(х) ділився націло на двочлен х-α.
• Наслідки:

1) Якщо {α₁, α₂ ,... α₂} – множина коренів многочлена А(х), який тотожно не дорівнює нулю, то А(х)=(х-α₁)·(х-α₂)·...· (х-α_n)·Q(х), де Q(х) – деякий многочлен.

2) Множина коренів многочлена степеня п містить не більше ніж п  елементів.

3) Якщо множина коренів многочлена

містить більше, ніж п  елементі, то  , тобто цей многочлен тотожно дорівнює нулю.

3. Розв’язування вправ

 Приклад 1. Доведіть, що вираз ділиться націло на многочлен .

Маємо: . Оскільки , то за теоремою многочлен А(х) ділиться націло на , тобто ділиться націло на многочлен

Приклад 2. Остачі від ділення многочлена Р(х)  на двочлени х-2 і х-з відповідно дорівнюють 5 і 7. Знайдіть остачу від ділення многочлена Р(х) на многочлен .

Оскільки степінь многочлена дорівнює 2, то степінь шуканої остачі не більша за 1. Тому остача – це многочлен виду . Маємо:

. Підставимо по черзі в цю рівність х=2 і х=3. Отримаємо: . Застосовуючи теорему Безу, маємо: Р(2)=5 і Р(3)=7. Тоді маємо систему . Звідси . Тоді шуканою остачею є многочлен .

• Робота «ланцюжком» біля дошки

Знайдіть остачу від ділення многочлена А(х) на двочлен В(х):

1)

2)

3)

4)

Доведіть, що многочлен А(х) ділиться націло на двочлен В(х)

1)

2)

3)

4)

• Завдання підвищеного рівня

При яких значеннях параметрів многочлен А(х) ділиться націло на многочлен В(х):     ?

4. Домашня робота (на картках)

• Доведіть, що многочлен А(х) ділиться націло на двочлен В(х)

1)

2)

3)

• При яких значеннях параметрів 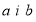многочлен А(х) ділиться націло на многочлен В(х):   ;

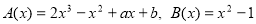Використані джерела:

1. Алгебра підручник для 8 класу з поглибленим вивченням математики,

А.Г. Мерзляк,  В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009

Презентація 1

Презентація 2