Урок на тему: "Кути, утворені при перетині двох прямих січною. Ознаки паралельності прямих."

Тема уроку: Кути, утворені при перетині двох прямих січною. Ознака паралельності прямих.

Мета уроку:

Навчальна:

• Сформувати поняття учнів про січні й види кутів, утворених при перетині двох прямих січною.
• Сформувати поняття учнів про зміст теорем про ознаки паралельності прямих і наслідки цих ознак.
• Сформувати вміння визначати на рисунку внутрішні односторонні кути, внутрішні різносторонні і відповідні кути, утворені при перетині двох прямих січною.
• Учити застосовувати ознаки паралельності прямих і наслідки з них  при доведенні й розв’язуванні задач.

Розвивальна:

• Розвивати пізнавальний інтерес до геометрії;
• вміння використовувати власний досвід;
• вміння організовувати навчальну працю;
• формувати логічне, абстрактне, системне мислення.

Виховна:

• Сприяти підтримці на високому рівні загальної працездатності до навчання;
• виховувати волю і наполегливість в учнів для досягнення кінцевих результатів;
• виховувати спостережливість, кмітливість.

Обладнання:

• мультимедійний проектор, презентація до уроку, роздатковий матеріал.

Хід уроку

1. Організаційний момент

• Доброго дня! Я вас вітаю на уроці геометрії – уроці, що підтвердить слова Миколи Яругіна: «І математика безмежно різноманітна і міститься в усьому».

2. Підготовка до свідомої навчальної праці

Досягти успіху можна тільки тоді, коли є певна мета. Тому скористаємось планом вивчення теми, ознайомимось з ним та за цим планом сформулюємо мету нашого уроку.

План вивчення теми

1. Означення січної відносно двох прямих.
2. Види кутів, утворених при перетині двох прямих січною.
3. Ознаки паралельності прямих та наслідки з неї.

Підготуємо наші зошити до роботи. Хочу нагадати, що під час роботи з діловими документами запорукою успіху є старанне, охайне, уважне ставлення до ціє роботи. (Запис дати, теми.)

IІІ. Актуалізація опорних знань

Повторимо означення, теореми, аксіоми, які будуть нам потрібні протягом уроку під час вивчення нової теми. В картці контролю теоретичних знань №1 замість пропусків вставте потрібні слова. Правильна відповідь оцінюється одним балом.

Картка контролю теоретичних знань №1

• Дві прямі, які лежать у площині, називаються паралельними, якщо вони ________.
• Через точку, що не _________ , на даній прямій, можна провести на площині не більш як одну пряму, ______ даній прямій.
• Дві прямі називаються перпендикулярними, якщо вони перетинаються під _______ кутом.
• Через кожну точку прямої можна провести перпендикулярну до неї ______ і до того ж тільки _______.
• Два кути називаються суміжними, якщо одна сторона у них ______, а дві інші сторони цих кутів є ______ променями.
• Два кути називаються вертикальними, якщо сторони одного кута є _______  ______ сторін другого.

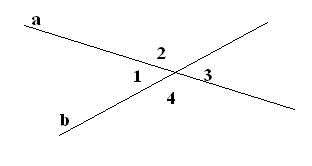
• < 1 + < 2 = ?
• <1 = < ?
• <2 = < ?
• <2 + < 3 = ?
• < 1 + < 4 = ?
• < 1 + <2 + <3 + <4 = ?

Наведіть приклади із оточення, які можуть бути моделями паралельних прямих. (Учні наводять свої приклади.)

Паралельність прямих дуже часто зустрічається у навколишньому світі: узбіччя доріг, лінії електропередач, береги річок.

Міст з’єднує береги річки, але річку – перетинає, тобто міст перетинає лівий та правий береги в двох місцях. Створимо математичну модель цієї картини. Так, як береги річки паралельні – накреслимо дві паралельні прямі (a| | b), міст перетинає береги річки в двох місцях – проведемо пряму с, яка перетинає пряму а в точці А, пряму b в точці B. Давайте зробимо висновок із даної моделі про пряму с. Вона називається січною. То яке ж визначення має січна?

Пряма с називається січною відносно прямих а і b, якщо вона перетинає їх у двох точках.

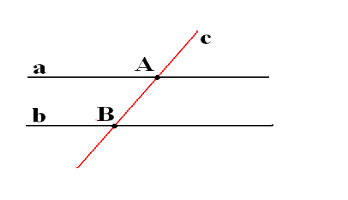
a| | b

c    a в точці А

c    b в точці B

Кути, утворені при перетині двох прямих січною

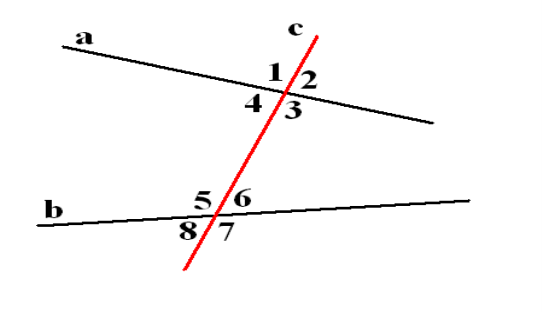
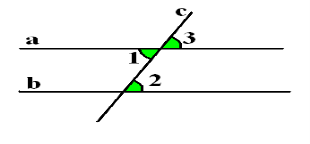
При перетині прямих а і b січною с утворилося вісім кутів.

• Як ви вважаєте, які з кутів, що зображені на рисунку, можна назвати внутрішніми, а які зовнішніми? (Внутрішні кути – 3, 4, 5, 6 і зовнішні – 1, 2, 7, 8.)
• Які з кутів, що зображені на рисунку, можна назвати односторонніми? (1, 3, 5, 7 і 2, 4, 6, 8.)
• Які з цих кутів внутрішні односторонні, а які - зовнішні односторонні? (Внутрішні односторонні  - 3 і 5 та 4 і 6; зовнішні односторонні – 1 і 7 та 2 і 8.)
• Які з кутів, що зображені на рисунку, можна назвати внутрішніми різносторонніми, а які - зовнішніми різносторонніми? (внутрішні різносторонні: 3 і 6 та 4 і 5, зовнішніми різносторонніми: 1 і 8 та 2 і 7.)

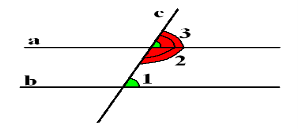
Дамо визначення внутрішнім одностороннім, внутрішнім різностороннім та відповідним кутам.

Внутрішніми односторонніми кутами називаються кути, які лежать з одного боку від січної с між прямими а і b.

Внутрішніми різносторонніми кутами називаються кути, які лежать з різних боків від січної с між прямими а і b.

Відповідні кути лежать з одного боку від січної с, причому сторона одного з них частиною сторони іншого.

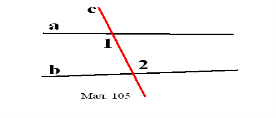
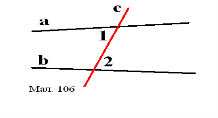
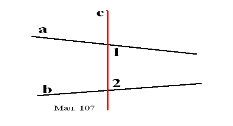
Вправа № 132

Як називаються кути 1 і 2 на рисунках 105 – 107?

Історична довідка

В першій книзі “Начала”  Евкліда  (давньогрецький вчений III ст. до н.д.) подано про ознаку  паралельності двох  прямих.

Наступний матеріал є дуже важливим у житті та побуті, про свідчить такий факт. При прокладання залізничної або трамвайної колій паралельність має вирішальне значення (непаралельність призводить до аварій).

Ознака паралельності прямих і наслідки з неї

Теорема. Якщо при перетині двох прямих січною  відповідні кути рівні, то прямі паралельні.

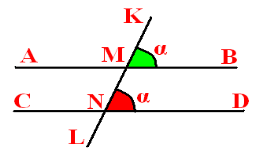
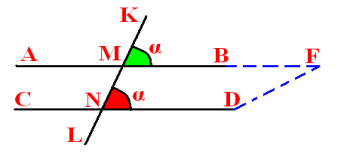
Доведіть, що прямі а і b паралельні.

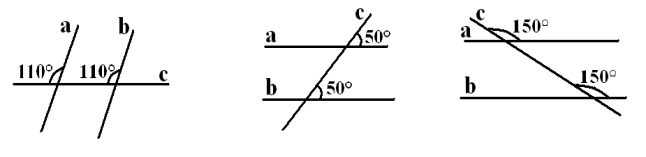
Наслідок 1

Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні, то прямі паралельні.

<1 = <2

<1 = <3, бо вони ________.

Отже, <2 = <3, бо вони ________.

За ознакою паралельності прямих маємо: a || b

Наслідок 2

Якщо при перетині двох прямих січною сума внутрішніх односторонніх кутів дорівнює 180°, то прямі паралельні.

<1 + <2 = 180°

<2 i <3 – суміжні, тому <2 + <3 = ______.

< 1 = <3, бо вони _____ .

За ознакою паралельності прямих маємо: a || b

Наслідок 3

Дві прямі, перпендикулярні до третьої прямої, паралельні.

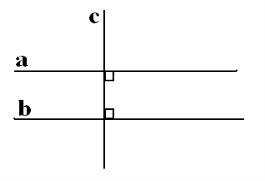
а   ┴   b

b  ┴   c

Враховуючи наслідок 2 маємо а || b. 

Чи паралельні прямі а і b?

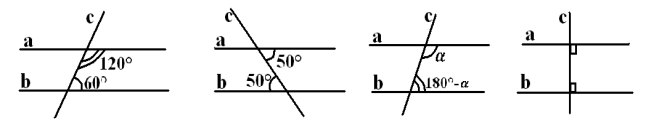
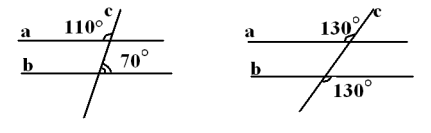
Задача №136

Якими є прямі  a  і  b (паралельними чи прямими, що перетинаються)?

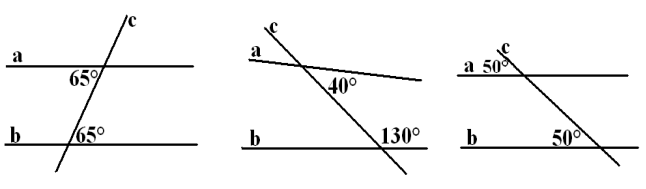
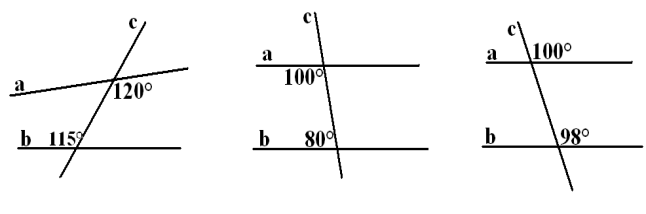
Задача №137 (письмово)

На рисунку визначено міри двох кутів, що утворилися при перетині прямих m і n січною  p. Обчисліть міри всіх інших кутів, що утворилися. Чи паралельні прямі m і n?

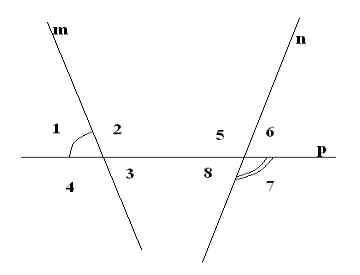
Дано: < 1 = 70º

          < 7 = 120º

1. Знайти: < 2, < 3, < 4, < 5, < 6, < 8.
2. Довести: m | |  n.

Розв’язання

1. < 1 = < 3 = 70º - вертикальні

< 1 і < 4 – суміжні; < 4 = 180º - 70º = 110º  

< 4 = < 2 = 110º - вертикальні

< 5 = < 7 = 120º- вертикальні

< 5 і < 6– суміжні; < 6 = 180º - 120º = 60º 

 < 6 = < 8 = 60º - вертикальні

2. < 1 і < 5 – відповідні, < 1 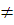< 5, то звідси випливає, що прямі m і  n не паралельні.

Відповідь: 1)< 1 = < 3 = 70º; < 4 = < 2 = 110º; < 5 = < 7 = 120º; < 6 = < 8 = 60º;

                   2) прямі m і  n не паралельні.

Підсумок уроку

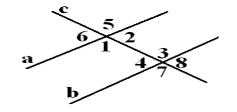
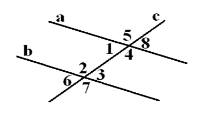
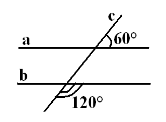
Пряма с пертинає прямі а і b, як показано на рисунках. Визначте істинність тверджень (якщо твердження істинне, поставте знак»+», якщо хибне «-»):

<1 = <3,то а||b

<1 + <2 = 180°, то а||b

<1 + <4 = 180°, то а||b

<3 = <4, то а||b

<5 = <3, то а||b

<5 + <3 = 180°, то а||b

<8 =<3, то а||b

<8 + <3 = 180°, то а||b

<6 = <7, то а||b

<6 + <7 = 180°, то а||b

<6 = <8, то а||b

<5 + <8 = 180°, то а||b

Відповіді

Рефлексія.

• Які математичні терміни з'явилися в твоєму словнику?
• Я добре навчився …, необхідно попрацювати над …
• Що викликало здивування на уроці?
• Кому ти хочеш подякувати за роботу?
• Передати свій емоційний стан за допомогою трьох прикметників.

Домашнє завдання

1. Вивчити ознаки паралельності прямих, наслідки (параграф 9 підручника).

2. Рівень А: №133, 135.

Рівень Б: №138, 147.

Рівень В: №148, 152.