Урок на тему "Ділення многочленів "

Цикл уроків з алгебри на тему «Основи теорії подільності»

для 8 класів з поглибленим вивченням математики 

                підготувала вчитель математики

 НВК: Гайсинська СЗШ-інтернат І-ІІІ ступенів  - гімназія

 Дем´янюк Ганна Володимирівна

Урок №12

Тема: Ділення многочленів

Мета: Вдосконалити вміння учнів ділити многочлени методом «кута», подавати раціональний дріб у вигляді суми многочлена і правильного дробу;

Тип уроку: урок формування умінь і навичок

Обладнання: підручник, картки.

Хід уроку:

1. Актуалізація опорних знань

 - Метод незакінченого речення:

1. Многочлен А(х) ділиться націло на тотожно не рівний нулю многочлен В(х), якщо….

2. Якщо многочлен А(х) ділиться націло на многочлен В (х), то це позначають…

3. Якщо ,  то степінь многочлена дорівнює …

4.  Для будь-якого многочлена А(х) і многочлена В(х), який тотожно не дорівнює нулю, існує єдина пара многочленів Q(х) і R (х) таких, що…

5. Подання раціонального дробу у вигляді суми многочлена і правильного дробу називають….

2. Перевірка домашньої роботи

1. Доведіть, що  многочлен А(х) ділиться націло на многочлен В (х):

1)       Відповідь:

2)

Відповідь:

2. Поділивши «кутом» многочлен А (х) на многочлен В (х), знайдіть неповну частку й остачу

1)

Відповідь:

2) Відповідь:

 

 

3. Виділіть цілу частину з раціонального дробу:

1) Відповідь:

    2)

Відповідь:

4. Доведіть, що вираз 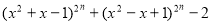ділиться націло на вираз 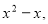де 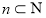 (високий рівень)

Відповідь: перевірити подільність при х=0 і х=1

3. Розв’язування  вправ

- робота в групах (по 4 учня, завдання на картках,  достатній рівень)

1. Доведiть, що (х⁴ + 5х³ + 5х² -1)(х+1).

2. Знайдiть остачу вiд ділення P(x) на S(x), якщо

   а) P(x) = 3х⁶ +2х⁴ – 7,  S(x) = х⁵ – 7х⁴ +3х² + х;

   б) P(x) = 6х⁴ +5х³ +15х² + х -10, S(x) = 2х³ + 3х² + 7х – 5.

   в) P(x) = 2х⁴ +3х³ – 5х² - 7х + 2 ,  S(x) = х – 3.

- робота з класом (завдання високого рівня)

• При яких значеннях m многочлен х⁶ + х³ + m дiлиться на х³ +2?
• При яких значеннях a i b многочлен х³ + 2х² + ах +b дiлиться

   на х² + х + ab?

• P(x) = х³ +ах² + bх + ab. Знайдiть значення a i b, якщо при дiленнi P(x) на (х – 3) остача дорівнює   5, а на (х – 1) — остача дорiвнює 7. Чому дорiвнює остача вiд ділення P(x) на (х – 3)(х – 1)

4. Самостійна робота

(на картках)

Варiант 1

1. Знайдiть частку i остачу вiд дiлення P(x) на S(x), якщо:

   а) P(x) = 2х³ + х² – 2,  S(x) = х + 4;

   б) P(x) = 3х⁴ – 3х³ + 2х + 5, S(x) = х² + х – 2;

   в)х³ – 2х² – 3х +6, S(x) = х – 3.

 

Варiант 2

1. Знайдiть частку i остачу вiд дiлення P(x) на S(x) , якщо:

   а) P(x) = х⁴ + 5х² + 6,  S(x) = х + 2;

   б) P(x) = 2х⁴ – х³ – 3х² – 3, S(x) = 2х² – х  + 2;   

   в) 3х³ – х² – 4х – 2 , S(x) = х + 1.

 

5. Домашня робота

1. Знайдiть остачу вiд дiлення P(x) = х⁵ – 3х² + 7х +2 на S(x) = х +2.

2. Доведiть, що многочлен P(x) = (х – 2)¹⁰⁰ + (х – 1)⁵⁰ -1 дiлиться на

 S(x) = х² – 3х + 2.

3. (високий рівень) Знайдiть НСД (P(x); S(x)), якщо

   а) P(x) = 3х³ +6х² – х – 2,  S(x) = х² +3х + 2;

   б) P(x) = 2х³ - 5х² – 8х + 20, S(x) = х³ + х² – 4х – 4.

 

Використані джерела:

1. Алгебра підручник для 8 класу з поглибленим вивченням математики,

А.Г. Мерзляк,  В.Б. Полонський, М.С. Якір, - Харків, «Гімназія», - 2009

2. Алгебра та початки аналізу 10 клас, профільний рівень

А.Г. Мерзляк, Д.А. Номіровський,  В.Б. Полонський, М.С. Якір, - Харків «Гімназія», - 2010

3. О.Ю. Карік, Матеріали для факультативних занять, спецкурсів, гуртків, математика 5-7, Харків, - «Основа», -  2008