урок на тему: "Подібність трикутників"
Тема. Подібність трикутників
Мета: освітня: сформувати уявлення про подібні фігури, поняття подібних трикутників, вміння знаходити невідомі елементи подібних трикутників;
розвиваюча: розвивати логічне мислення, математичну грамотність мовлення, культуру креслень;
виховна: виховувати пізнавальну активність, культуру спілкування, формування культури праці, сумлінного ставлення до матеріальних і духовних цінностей.
Тип уроку: засвоєння нових знань, умінь, навичок.
Обладнання: комп’ютер, презентація, моделі фігур, роздатковий матеріал, аркуш самоконтролю, креслярське приладдя.
Епіграф уроку.
Навчання мистецтву розв’язувати задачі – це виховання волі. (Д. Пойа)
Очікувані результати:
Після уроку учні зможуть:
- дати означення подібних трикутників;
- формулювати ознаки подібності трикутників та ознаки подібності трикутників;
- свідомо застосовувати вивчений матеріал під час розв’язування задач;
- робити логічні висновки, аналізувати вивчений матеріал;
- творчо мислити та самостійно працювати.
ХІД УРОКУ
- Організаційний момент
- Привітання з класом.
- Учні готуються до уроку.
- Мотивація навчальної діяльності, повідомлення теми, мети уроку.
Тема нашого уроку «Розв’язування задач на застосування подібності трикутників», тому епіграфом до уроку я взяла слова великого Пойа «Навчання мистецтву розв’язувати задачі – це виховання волі». Видатний французький математик Жан Лерон Д’аламбер помітив, що «математика щедра, вона часто дає більше, ніж у неї просять».
Уявіть собі, що ви пішли зустрічати Новий рік у ліс. Побачивши найвищу ялинку, вирішили її прикрасити гірляндою і, головне, яскравою зіркою. Знаючи свої фізичні можливості, ви зрозуміли: щоб не витрачати зайвих зусиль, потрібно спочатку з’ясувати чи це можливо.
Проблема? Так! Наше життя складається із таких маленьких проблем, які ми можемо на сьогоднішній день розв’язати, використовуючи ті знання, яких набуваємо під час уроків.
Отже маємо конкретну мету: знайти висоту ялинки, не піднімаючись на вершину.
Мета уроку – навчитися застосовувати ознаки подібності трикутників до розв’язування задач. І я сподіваюсь, що наприкінці уроку ви зможете розв’язати цю проблему.
- Як можна назвати одним словом пари об’єктів? (Слайд 3) (подібні, схожі, однакові, пропорційні) (вчитель записує синоніми на дошці)
-
Усі ці об’єкти – подібні. Почнемо вивчення подібних фігур з вивчення подібних трикутників. Тому тема сьогоднішнього уроку: Подібні трикутники. (Слайд 4)
- щоб розібратися з подібними фігурами, дуже важливо почати вивчення з трикутників, як найпростіших багатокутників;
- знання властивостей подібних трикутників допоможе вам у розв’язанні інших важливих геометричних задач;
- Пригадаємо історію. Фалес Мілетський. (Слайд 5)
За переказами, Фалес виміряв висоту піраміди за довжиною її тіні в той момент, коли довжина тіні піраміди дорівнювала висоті самого Фалеса. Як ви думаєте, на що він спирався у своїх міркуваннях?
-
Знання властивостей подбних фігур, зокрема трикутників допоможе нам дати відповіді на запитання: (Слайд 6)
- Як знайти висоту дерева?
- Як знайти висоту будь-якого недоступного об'єкта?
- Як знайти відстань до недоступного об'єкта?
- Як виміряти ширину річки?
- Чому з маленького негативу виходить велика якісна фотографія?
- Як фокусна відстань впливає на чіткість зображення?
Та інші.
- Актуалізація опорних знань
Інтерактивна технологія «Інтерв’ю».
Один «учень-журналіст» збирає матеріал для математичної стіннівки.
- Сформулюйте означення трикутника?
(Трикутником називають фігуру, яка складається з трьох точок, що не лежать на одній прямій, і трьох відрізків, які сполучають ці точки.)
- Назвіть основні елементи трикутника?
(Сторони, вершини, кути)
- Види трикутників залежно від сторін?
- (Рівносторонні, різносторонні, рівнобедрені)
- Що називають периметром трикутника?
(Суму довжин усіх сторін трикутника)
- Які види трикутників розрізняють залежно від кутів?
(гострокутні, прямокутні, тупокутні)
Отже, ми повторили трикутник і його елементи, а зараз пропоную перейти до застосування цих знань у розв’язування базових задач, які нам допоможуть у більш складних ситуаціях.
З метою успішного засвоєння учнями означення, а також доведення властивостей подібних трикутників, учням слід активізувати знання і вміння щодо понять «рівні трикутники», «відповідні елементи трикутників», пригадати властивості кутів трикутника. Для цього пропонуємо учням виконати усні вправи.
1. ΔАВС = ΔА1В1С1. (Слайд 1)

Які трикутники зображені на слайді?
Назвіть рівні елементи трикутників?
Які кути трикутників є відповідними?
Які сторони трикутників є відповідними?
- ΔАВС = ΔМNK. (Слайд 2)
Назвіть рівні елементи трикутників?
Яку властивість ми використовуємо, щоб назвати рівні сторони?
- Чи можуть кути трикутника дорівнювати 20о, 80о, 100о? Чому?
- Яка властивість кутів трикутника?
- Вивчення нового матеріалу
§13, с. 83
У повсякденному житті трапляються предмети однакової форми, але різних розмірів, наприклад, футбольний м’яч та металева кулька, картина та її фотознімок, літак і його модель, географічні карти різного масштабу. У геометрії прийнято називати подібними. Так подібними між собою є всі квадрати, усі круги, усі відрізки.
Взагалі, подібність фігури – це схожість. Сформулюємо означення подібних трикутників.
Два трикутники називають подібними, якщо у них рівні кути, а відповідні сторони пропорційні.
Розглянемо два трикутника у яких рівні кути
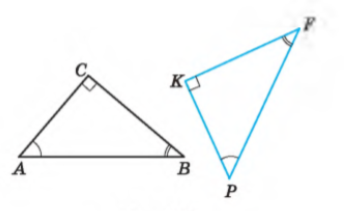 Позначимо перший АВС, а інший РKF. Отже, якщо у двох трикутників рівні кути, а відповідні сторони пропорційні.
Позначимо перший АВС, а інший РKF. Отже, якщо у двох трикутників рівні кути, а відповідні сторони пропорційні.
Наприклад:
А=Р, С=К, F=В.
Тепер відношення сторін:
1. Пропорційні відрізки.
Практична робота: знайдіть відношення відрізків (учні роблять відповідні записи у зошит)(Слайд 8)
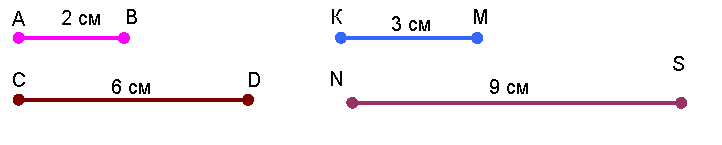
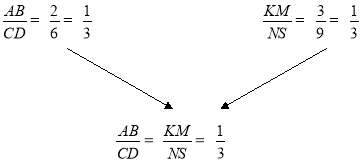
Говорять, що відрізки АВ та СD пропорційні відрізкам КМ та NS, якщо їх відношення рівне.
2. Подібні трикутники.
Практична робота: перед вам два трикутники, дослідіть їх завдання 1), 2) (Слайд 8)
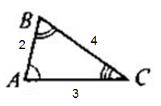
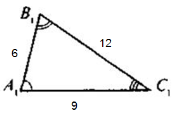
- Як можна назвати відповідні сторони трикутника? (пропорційні)
- Як можна назвати ці два трикутника? (подібні)
- Використовуючи дослідження спробуємо сформулювати означення подібності трикутників.
Означення: Два трикутники називаються подібними, якщо в них відповідні кути рівні, а відповідні сторони пропорційні.(Слайд 9)
1. Учні виконують малюнок у зошиті та записують:
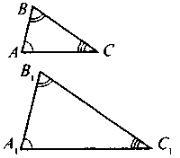 ΔАВС ~ ΔА 1В 1С 1
ΔАВС ~ ΔА 1В 1С 1 ![]()
![]() A =
A = ![]() A1,
A1, ![]() B =
B = ![]() B1,
B1, ![]() C =
C = ![]() C1;
C1;
![]()
2. Учні записують, як виражаються сторони одного з подібних трикутників через коефіцієнт подібності та сторону іншого трикутника.
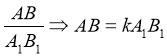
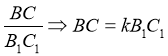
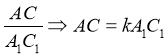
3. Повернемося до практичної роботи: виконаємо завдання 3)
Знайдіть відношення ![]() та
та ![]() .
.
 Який висновок можна зробити?
Який висновок можна зробити?
![]() =
= ![]()
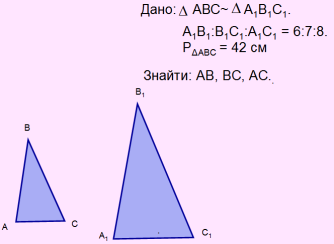
 4) Знайдіть периметри трикутників: АВС та А1В1С1, та їх відношення:
4) Знайдіть периметри трикутників: АВС та А1В1С1, та їх відношення: 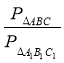 . Який висновок можна зробити?
. Який висновок можна зробити?
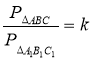
- Формування умінь, навичок (робота з підручником)
Умови задач пропонуються у вигляді презентації. Учні розв’язують задачі усно, із докладними міркуваннями та коментарями. Обрані літери правильних відповідей учні записують у зошити. Потрібно скласти ключове слово із літер правильних відповідей до задач.
№ 453 (усно)
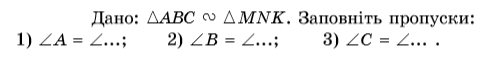
Розв’язання:
ABC MNK
- A = M;
- B = N;
- C = K.
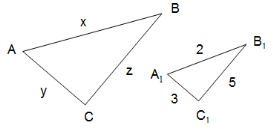
№ 455 (письмово)
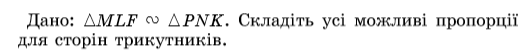
Розв’язання:
MLF PNK. Тому ![]()
№ 456 (письмово)
![]()
Розв’язання:
MNL ABC
M = A = 40o;
N = B = 80o;
L=C = 180o – (40o+80o)=60o
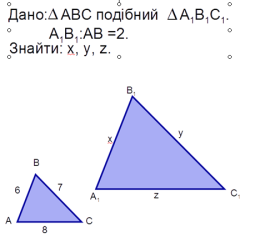
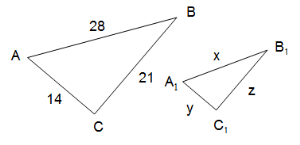
№ 458 (письмово)
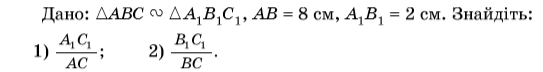
Розв’язання:
ABC A1 B1 C1
AB=8 см, A1 B1=2 см
-
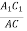 =
= 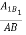 =
= 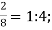
-
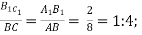
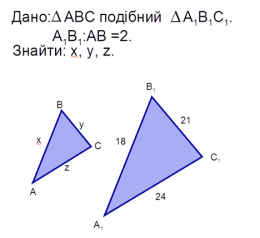
№ 461 (письмово)
- 7х = 21; х=3 (см)
8 · 3 = 24 (см)
9 · 3 = 27 (см)
- 9х – 8х = 5; х=5
7 · 5 = 35 (см)
8 · 5 = 40 (см)
9 · 5 = 45 (см)
- 7х + 8х + 9х = 48
24х = 48
х = 2
7 · 2 = 14 (см)
8 · 2 = 16 (см)
9 · 2 = 18 (см)
Відповідь: 1) 24 см; 27 см; 2) 35 см; 40 см; 45 см; 3) 14 см; 16 см; 18см.
Розв'язування усних задач: (Слайди 10-15)
Слайд 15 з повним розв’язанням.
|
|
|
|
|
|
|
|
|
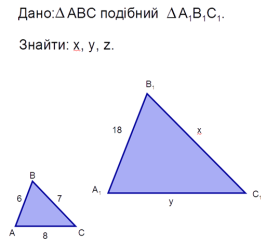
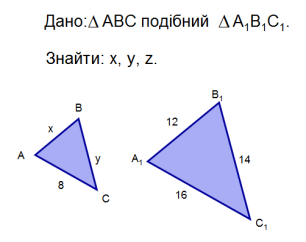
Самостійна робота із взаємоперевіркою
|
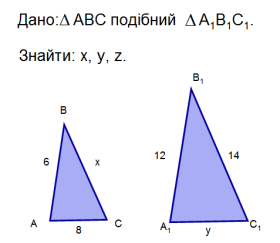
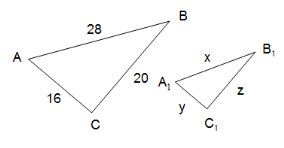
Варіант 1 ΔАВС ~ ΔА 1В 1С 1 Знайти х, у, z. |
Варіант 2 ΔАВС ~ ΔА 1В 1С 1 Знайти х, у, z. |
||
|
1. |
k = 3 |
1. |
k = 4 |
|
2. |
k = 7 |
2. |
k = 4 |
|
3. |
|
3. |
|
Відповіді:
|
Варіант 1 |
Варіант 2 |
|
1. х = 6, у = 9, z = 15. |
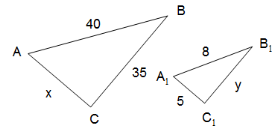
1. х = 8, у = 12, z = 20. |
|
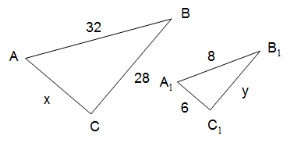
2. х = 4, у = 2, z = 3. |
2. х = 7, у = 4, z = 5. |
|
3. х = 24, у = 7. |
3. х = 25, у = 7. |
VІ. Підсумки уроку:
- Які трикутники називаються подібними?
- Які властивості подібних трикутників?
- Кут одного подібного трикутника дорівнює 100о, кут другого трикутника дорівнює 120о. Чи може таке бути?
- Чи можуть бути подібними тупокутний та прямокутний трикутники?
Домашнє завдання
Вивчити означення подібних трикутників та властивості подібних трикутників (з доведенням). Розв'язати задачі.
- На рисунку 6 ΔАВС ~ ΔА1В1С1. Заданими рисунка знайдіть х і у.

-
Відомо, що ΔАВС ~ ΔDEF. Знайдіть кут F, якщо
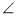 B = 80°,
B = 80°, 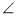 A =
A = 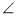 C.
C.
- Сторони трикутника дорівнюють 2,5 см, 4 см і 5 см. Знайдіть сторони трикутника, подібного даному, якщо його найменша сторона дорівнює найбільшій стороні даного трикутника.


про публікацію авторської розробки
Додати розробку