Урок на тему: "Подорожуємо Україною в пошуках арифметичної прогресії"

Тема: Подорожуємо Україною  в пошуках арифметичної прогресії

Мета:

Навчальна: узагальнення теоретичних знань з теми «Арифметична прогресія», вдосконалення навичок знаходження n-го члена та суми n- перших членів арифметичної прогресій за допомогою формул.

Розвивальна: розвивати пізнавальний інтерес учнів, вчити бачити зв'язок між математикою та оточуючим життям, розвивати математичне мовлення.

Виховна: виховувати почуття патріотизму.

Епіграф уроку: При вивченні наук приклади корисніше правил.

Хід уроку

І. Організація класу.

ІІ. Мотивація навчальної діяльності учнів.

 «Прогресія – це рух вперед» . Перша умова, якої треба дотримуватися в математиці, – це бути точним. Друга – бути чітким, і наскільки можливо, простим.

ІІІ. Повідомлення теми та мети уроку.

Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю узагальнимо знання з теми: « Арифметична прогресія», закріпимо навички обчислення елементів прогресії, покажемо зв’язок математики з оточуючим життям, мандруючи Україною,  будемо удосконалювати вміння оцінювати свої досягнення. Сьогодні ви не просто учні, а і мандрівники, які,  подорожуючи нашою країною, будуть шукати галузі застосування арифметичної прогресії.

ІV. Актуалізація опорних знань. Перевірка домашнього завдання. 

1. Теоретична розминка.

Але перш ніж вирушити в мандрівку, впевнимося, що ви володієте знаннями з теми. Я пропоную вам скласти кластер з теми «Арифметична прогресія».

2. Тест.

1.     З вказаних послідовностей арифметичною прогресією є...

     а) 45; 15; 5; 0...;            б) 4; 9; 9; 4...;        

     в) 2; 4; 8; 16...;              г) 15; 17; 19; 21...

 2.  Якщо перший член арифметичної прогресії дорівнює 8, а різниця 3, то другий її член дорівнює...

                    а) 5;       б) 24;  в) 8/3;         г)  11

3.   Якщо третій член арифметичної прогресії    дорівнює 15 і різниця 4, то четвертий її член дорівнює...

   а)  11;      б) 60;     в) 19;      г) 15/4

4. У заданій арифметичній прогресії 3; 7; 11; 15 другим членом є число...

   а) 3;         б) 7;         в)  10;         г) 4

5. Якщо арифметична прогресія (an) зростаюча, то...

     а) а₁< а₂;  б) а₁ > а₂;в) a₁ = a₂;г) а₁ ≥ а_2;    г) інша відповідь.

6.  Щоб знайти різницю арифметичної прогресії 4; 7; 10; 13;..., треба...    

а) 4 + 7;      б) 4 • 7;       в) 4 – 7;     г) 7 – 4

7. Щоб обчислити а₁₁, якщо а₁=3,d = 8, необхідно...

 а) 3+(8-1)11;        б)   8+(11–1)3;   

в) 3+(11-1)8;    г) 8+(3–1)11

8.  Якщо задана арифметична    прогресія і а₁ +а₂₁= 54, то сума а₂ +а₂₀ дорівнює...

   а) 22;    б) 18;     в) 54;    г) 108.

 9.  Якщо а₁=11, а₁₅=89, то,  щоб  обчислити S₁₅, треба...

а)   (15+11)/2*89;         б) (15+89)/2*11;

          в)   (15+11)/89*2;        г) (89+11)/2*15

10. Кого із вчених називали “Королем математики”

          а) Ломоносова;    б) Гаусса;   

          в) Піфагора;         г) Галілея.

V. Узагальнення та систематизація знань.

1. Першими на зв’язок з нами виходить група, яка помандрувала до м.Дніпра.

Учні: Ви запитаєте нас, чому ми вирішили обрати саме це місто. Відповімо: наша група завжди хотіла відвідати найвідомішу в наш час лікарню ім. Мечникова. Там нам запропонували екскурсію до лабораторії. Ми звичайно задались питанням: «А до чого тут арифметична прогресія?». І ось, які задачі ми вирішили розв’язати.

Задача 1.

Кількість еритроцитів (з розрахунку на ) в крові людини становить на рівні моря . Через кожні підняття вгору їх кількість збільшується на . Скільки еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест ()?

Розв’язання:, . . За рекурентною формулою матимемо: , .

Відповідь: В крові людини буде мільйонів еритроцитів.

Задача 2.

Хворий приймає ліки за наступною схемою: у перший день він приймає 5 крапель, а кожен наступний день - на 5 крапель більше, ніж у попередній. Дійшовши до норми 40 крапель в день, він 3 дні п'є по 40 крапель ліків, а потім щоденно зменшує прийом на 5 крапель, довівши його до п'яти крапель в останній день. Скільки пляшок ліків треба купити хворому, якщо в кожній міститься 20 мл ліків (що становить 200 крапель)?

Розв’язок:

Складемо математичну модель задачі:

5, 10, 15, …, 40, 40, 40, 35, 30, … , 5

40=5+5(n-1)

n=8

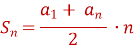
58 = (5 + 40) ∙ 8 : 2 = 180

180 крапель хворий приймає за схемою в перший період і стільки ж в другий. Всього ж він прийняв 180 + 40 + 180 = 400 крапель.

Всього хворий прийме 400 : 250 = 1,6 пляшечки.

Відповідь:  2 пляшки

2. А зараз нам звітують наші мандрівники зі столиці України.

Учні: А ми вирішили відвідати Національний банк України. Ми були в захваті від будівлі банку. Тому дуже захотілося дізнатися як арифметична прогресія пов’язана з банківською справою?

Задача 1.

Банк  пропонує кредит у 30 000 грн під 10% річних на залишок кредиту на 10 років зі щорічною виплатою 1/10 частини кредиту.  Обчислити всі відсоткові гроші.

Складемо послідовність щорічних виплат отриманого кредиту.

Кожний рік залишок кредиту зменшується на
30 000 ^.1/10 = 3000 (грн.)

Тоді відсоткові виплати за 1 рік становлять:

(30 000-3000) ^.0,1 = 2 700 (грн.)

За другий рік: (30 000 – 2 ^. 3 000) ^. 0,1 = 2 400 (грн.)

За третій рік: (30 000 – 3 ^. 3 000) ^. 0,1 = 2 100 (грн.)…

За дев'ятий рік: (30 000 – 9 ^. 3 000) ^. 0,1 = 300 (грн.)

За десятий рік: 0 грн.

Отже, отримали арифметичну прогресію, різниця якої 300 грн.

Тому, для обчислення всіх відсоткових грошей скористаємося формулою суми арифметичної прогресії:

S = (2700+300) : 2 ^. 9 = 13 500 (грн.)

Задача 2.

Джентльмен отримав спадок. Перший місяць він потратив $, а кожний наступний місяць він витрачав на $ більше, ніж за попередній. Скільки $ він витратив за другий місяць? Третій? Десятий?

Розв’язання:.     $, $,. . .     $.

Відповідь: За другий місяць джентльмен витратив 150$; за третій - 200$; за десятий місяць - 550$.

3. Тепер надаємо слово сонячній та веселій Одесі.

Учні:  А ми вирішили в своє життя впустити трошки гумору і  подивитися, а як же готуються до фестивалю гумору в Одесі. Але ми не забули і про арифметичну прогресію.

Задача 1.

Язиката Хвеська протягом мі­сяця (31 день) щодня розпо­відає в сільському клубі анек­доти про політику. Через утому кожного наступного дня кіль­кість анекдотів на 2 менше, ніж   попереднього. Скільки анекдотів почули від Хвеськи односельці, якщо першого дня  вона розказала їх рівно 100? (задача гумористичного змісту)

Розв’язання

а₁= 100 анекд, а d= - 2 анекд. Знайти S₃₁.

S₃₁==*31= 70*31= 2170 анекдотів

Відповідь:2170 анекдотів

Задача 2.

Дама здавала в багаж:

Диван ………..  кг

Валізу…   21 кг

Саквояж…….   кг          арифметична

Картину…   18 кг              прогресія

Корзину……..  кг

Картонку……..кг

                 І цуценятко…….. кг     Знайти,  скільки важить багаж.

Розв'язання

a_{2 =}  а₁ + d;  а_{1 =}   a₂ – d;  a_{4 =}  а₁ + 3d; ;  а₁₌  a₄ - 3d; a₂ – d = a₄ - 3d; a₂ – a₄= d - 3d;

-2d= 21-18; d= - 1,5.  Диван : а₁=21 – (- 1,5) = 22,5 кг. Саквояж : 18 – (-1,5) =19,5 кг; корзина:18-1,5=16,5 кг; картонка:16,5-1,5=14,5 кг; і цуценятко: 14,5-1,5= 13 кг.  S=126

Відповідь:126 кг

4. Вітаємо зелені Карпати.

Учні: Кожен українець хоча б раз у житті мріє відвідати захід нашої країни. А саме: місто Львів та чарівні Карпати. Тут ми побували не тільки у лісі, а й сходили на рибалку і звичайно не забули про завдання.

Задача 1.

 При зберіганні колод будівельного лісу їх укладають так, як показано на малюнку. Скільки колод знаходиться в одній кладці, якщо в її основу покласти 12 колод?

Розв’язання

а₁= 12 колод, d = -1.n = 12. Знайти S_12.    

S₁₂= (2а₁ + (12-1)*d):2*12 = (24+11*(-1)):2*12 = 78 колод

Відповідь:78 колод.

Задача 2.

Олег, Петро, Сергій та Андрій ловили рибу. Кількість рибин, які вони впіймали, утворюють арифметичну прогресію. Найменше рибин – 9 – упіймав Петро, а найбільше – 18 – Олег. Скільки рибин упіймали Сергій та Андрій разом? Скільки всього рибин упіймали хлопці?

Розв'язання

В арифметичній прогресії а₁₊а_{n =} а_{2 +} а_{n-1 =} а₃₊ а_n-2. Тому Сергій та Андрій разом зловили 9+18=27 рибин. Хлопці зловили 54 рибини.

V. Підсумок уроку.

1. Рефлексія. «Комплімент».

Прогрес – це рух, це велич, це зростання,

Як Україні зараз він потрібний,

Прогресії – його сестриці рідні.

Це школа, математика, навчання.

І кожен з нас, як аксіому знає:

Без математики на ноги нам не стати

Тож хай лунає лозунг наш крилатий

Прогресу без прогресій не буває!

2. Самооцінювання

 

3. Домашнє завдання . Скласти задачу на дану тему ,яку вивчаємо в даний час.

Прізвище, ім’я
№ з/п		МАКСИМАЛЬНА КІЛЬКІСТЬ БАЛІВ	МІЙ БАЛ
1	Кластер	2
2	Тести	5 (0,5 – 1 питання)
3	Задачі	4 (0,5 – 1 задача)
4	Бонусний бал (доповнення, зауваження)	1
Всього: