Урок на тему "Показникова функція"

Тема: Показникова функція

Мета уроку:

1.     Освітня: Познайомити учнів із поняттям показникової функції, її властивостями та графіком. Розвивати навички розв’язання прикладів і задач з використанням показникової функції.

2.     Розвивальна: Розвивати логічне мислення, вміння аналізувати функції, будувати графіки.

3.     Виховна: Виховувати відповідальність, цікавість до математичних досліджень.

Обладнання:

1.     Презентація з графіками функцій та схемами.

2.     Графічний калькулятор або інтерактивна дошка.

3.     Робочі зошити та таблиці властивостей функцій.

Хід уроку

І. Організаційний момент (2 хвилини)

•       Привітання, перевірка присутніх, налаштування на роботу.

ІІ. Актуалізація знань (5 хвилин)

•       Повторення властивостей степеневої функції та основних понять.

•       Питання до класу:

o    Що таке основа степеня?

o    Які властивості мають степеневі вирази?

•       Висновок: показникова функція є природним продовженням степеневої функції, коли показник змінний.

ІІІ. Мотивація навчальної діяльності (3 хвилини)

•       Демонстрація застосування показникової функції у реальному житті (зростання популяції, фінансові розрахунки, радіоактивний розпад).

•       Мета уроку: дізнатися, як виглядає і як поводиться показникова функція, а також навчитися використовувати її для розв’язання прикладних задач.

IV.          Подання нового матеріалу (15 хвилин)

1.     Означення показникової функції:

o    Формула:  o Пояснення, що а  – це основа, яка є сталою, а  х – змінна.

2.     Властивості показникової функції:

o    Область визначення:  

o    Область значень:  o Монотонність:

▪     Якщо  – функція зростаюча.

▪     Якщо  – функція спадна.

o    Нулі та перетини з осями:

▪     Функція не має нулів,  o Асимптоти:

▪     Функція має горизонтальну асимптоту  o Поняття експоненціальної функції з основою е.

3.     Графік показникової функції:

o    Побудова графіків функцій  для порівняння.

o    Обговорення відмінностей та властивостей залежно від значення основи a.

V.              Закріплення нового матеріалу (10 хвилин)

1.     Практична робота в зошитах:

o    Побудуйте графіки функцій:

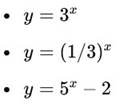
o    Аналіз результатів: як змінюється графік при зміні значення a та при зсуві по осі y.

2.     Групова робота:

o    Дати учням завдання знайти в Інтернеті приклад застосування показникової функції (в економіці, фізиці тощо) і коротко описати.

VI.          Формування навичок і вмінь (15 хвилин)

1.     Розв'язання задач:

o    Задача 1: Знайдіть значення функції  

o    Задача 2: Для популяції бактерій кількість бактерій подвоюється кожні 3 години. Запишіть формулу для опису цього процесу. o Задача 3: Якщо початкова сума на рахунку зростає на 5% щорічно, знайдіть формулу, яка описує стан рахунку через t років.

2.     Творче завдання:

o    Пояснити студентам, як змінюється функція при різних значеннях a і як це можна застосувати в реальних ситуаціях.

VII.      Підсумок уроку (5 хвилин)

•       Повторення основних властивостей та графіків показникової функції.

•       Питання до класу:

o    Які основні властивості показникової функції? o Де в житті можна побачити застосування показникової функції?

        •     Підведення підсумків, відповіді на питання учнів.

VIII.   Домашнє завдання

•       Виконати задачі на побудову графіків та вирішення рівнянь з показниковими функціями.

•       Дослідити застосування показникової функції у своєму оточенні (економіка, наука) і написати короткий звіт на 5-6 речень.