Конспект уроку у 6 класі на тему:

«Прямокутна система координат. Координатна площина.»

                                                                            Підготувала

                                                                           Вчитель математики                                                                                                                                                                              

                                                                            Миколаївської ЗОШ №2  I-III ст.                                                                           

                                                                            Івашків Марія Василівна

Мета уроку:  навчальна  навчити учнів будувати точку за її координатами                   і визначати координати точки, позначеної на координатній площині.

розвиваюча  розвивати логічне мислення.

виховна виховувати самостійність, уміння працювати охайно,   зосереджено.

Задачі уроку:

• ознайомити учнів з прямокутною системою координат на площині;
• навчити орієнтуватися на координатній площині, чітко і акуратно виконувати геометричні побудови;
• розвивати творчі здібності;
• виховувати інтерес до предмету

Тип уроку: Формування умінь і навичок.

Обладнання: мультимедійна дошка, презентація до уроку у Mikrosoft Power Point, кросворд.                           

Щоб щось пізнати,

Треба вже щось знати

                                                                                       Станіслав Лем                                                                                                                      

Хід уроку

1. Організаційний момент

Вітання вчителем учнів. Оголошення теми, мети, форми проведення уроку.

ІІ. Повторення вивченого матеріалу

• За даним рисунком дайте відповіді на запитання.
• Які прямі називаються паралельними?
• Які прямі називаються перпендикулярними?
• Визначіть на ваш погляд, які прямі перпендикулярні? Паралельні? Яким інструментом можна перевірити ваші відповіді?

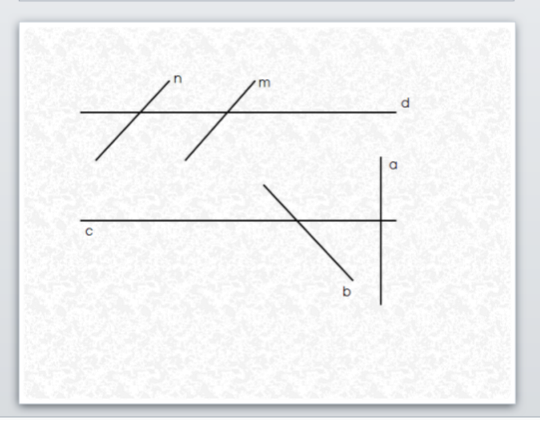
1. Яка пряма називається координатною?
2. Якими числами визначаються координати точок, розташованих справа від початку координат? Зліва від початку координат?
3. Яку координату має початок координат?
4. Скільки чисел визначають положення точки на координатній прямій?

Назвіть координати точок, зображених на рисунку. Як записати їх координати?

III. Вивчення нового матеріалу

Звертаючись один до одного, люди часто говорять: «Залиште свої координати». Для чого? Щоб людину можна було легко знайти. Це може бути: номер вашого телефону, домашня адреса, місце роботи. Суть системи координат полягає в тому, що це правило, за яким визначають положення об’єкта. Системи координат оточують нас усюди. Приведемо кілька прикладів:

•  шахова дошка;
• поле для гри «Морський бій»;

• географічні та зоряні карти;
• координатна сітка для пілотів, моряків.

         Ми з’ясували, що системи координат оточують практичне життя людини. Ідея координат зародилася в стародавні часи в зв’язку з потребою астрономії, географії, живопису. Використовувати координати в математиці вперше почав П’єр Ферма (1601-1665) і французький філософ, математик Рене Декарт (1596-1650).  Система координат дозволяє визначити положення того чи іншого об’єкту. На честь Декарта прямокутну систему координат називають ще прямокутною декартовою системою координат.

Що ж таке система координат?

              Проведемо дві перпендикулярні координатні прямі, які перетинаються в початку їх відліку – точці О й мають рівні одиничні відрізки . Ці прямі називають осями координат, точку О – початком координат. Горизонтальну координатну пряму називають віссю абсцис і позначають буквою х, вертикальну координатну пряму називають віссю ординат і позначають буквою у. Вісь абсцис і вісь ординат утворюють прямокутну систему координат. Площину, на якій задана прямокутна система координат, називають координатною площиною.

               Нехай точка А – точка координатної площини. Положення точки А на координатній площині визначається парою чисел (-3;2), які називаються координатами цієї точки. Щоб знайти ці координати, потрібно через т.А провести перпендикулярну пряму до осі абсцис, у їх перетині отримали т.В з координатою -3, і перпендикулярну пряму до осі ординат, а в їх перетині отримали т.С з координатою 2.Пара чисел  (-3;2) є координатами т.А. Першу координату -3 називають абсцисою цієї точки, а другу 2 – ординатою. Точка К має навпаки координати.

           Якщо точка лежить на осі абцис, то її ордината дорівнює нулю; якщо точка лежить на осі ординат, то її абсциса дорівнює нулю: М(4;0) і N(0;-2)

              Осі координат розбивають площину на 4 частини, які називають координатними чвертями. Нумерація чвертей і знаки координат зображено на рисунку.

IV Розв’язування вправ

1. Прочитайте записи: А(-1; 2); В(3; 0); С(-1; -1); D(0; -3).

Назвіть абсцису та ординату точок: M(-3; 2), N(-2;-3); K(0,5; 0,5).

2.А тепер ми з вами попробуємо визначити координати точок на площині, зображених на рисунку.

• Чому дорівнює абсциса точок А;С;F?
• Чому дорівнює ордината точок D,F,Z?
• У якій чверті лежать точки А,У,D?
• Запишіть координати усіх точок.

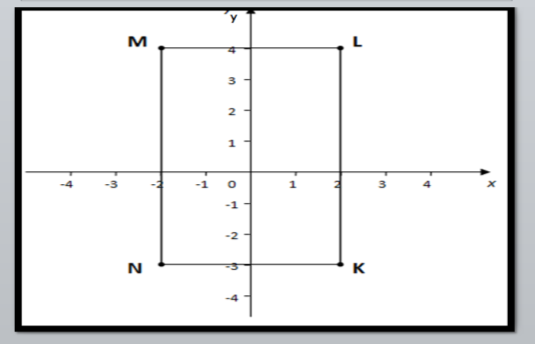
3.Додаткове завдання. Побудуйте точки  K(2;-3), L(2;4),M(-2;4) і                N(-2;-3). Сполучіть ці точки в такій послідовності:K,L,M,N,K. Яку фігуру ви отримали?

V. Підсумок

Знаючи, як знайти точку на координатній прямій, ми пізнали сьогодні, як знаходити положення точки на координатній площині .

1. Скільки чисел треба вказати, щоб задати положення точки на координатній площині?
2. Як називаються числа, які вказують положення точки на координатній площині?
3. Як називається перша координата?
4. Назвіть координати точки Р, якщо її абсциса дорівнює 0, ордината 5?
5. Чому дорівнює ордината точки А(-1;4)?

А на завершення нашого уроку пропоную розгадати кросворд, запитання до якого ви бачите на екрані.

Кросворд

По горизонталі:

1. О(0;0) – це … координат. (Відповідь: початок).
2. прямі Ох та Оу утворюють … координат. (Відповідь: систему).
3. пара чисел (3; 6) – це … точки. (Відповідь: координати).

По вертикалі:

1. Як називається число 2, якщо дано точку М (2;5). (Відповідь: абсциса).
2. Як називається для цієї самої точки число 5? (Відповідь: ордината).
3. Скільки точок задає на координатній площині пара чисел?. (Відповідь: одну).

VІ. Домашнє завдання

п.45, № 1336;1342

Література

1. Янченко Г.М., Кравчук В.Р. «Математика: Підруч. для 6 кл. -  Тернопіль: Підручники і посібники, 2006
2. Мерзляк А.Г, Полонський В.Б, Рабінович Ю.М.Якір М.С. Збірник задач і завдань для тематичного оцінювання з математики для 6 класу. – Х.: Гімназія, 2007

Верблюд

1) (- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4),  (- 3; 4), (0; 7), (2; 4),  (4; 7), (7; 4), (9; 3), (9; 1), (8; - 1), (8; 1), (7; 1), (7; - 7), (6; - 7), (6; - 2), (4; - 1), (- 5; - 1),  (- 5; - 7), (- 6; - 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).

2) Око: (- 6; 7).

Кінь

1) (14; - 3), (6,5; 0), (4; 7), (2; 9), (3; 11), (3; 13), (0; 10), (- 2; 10), (- 8; 5,5), (- 8; 3),  (- 7; 2),  (- 5; 3),  (- 5; 4,5),  (0; 4),  (- 2; 0),  (- 2; - 3),   (- 5; - 1),  (- 7; - 2),  (- 5; - 10), (- 2; - 11), (- 2; - 8,5), (- 4; - 8), (- 4; - 4), (0; - 7,5), (3; - 5).

2) Око: (- 2; 7).

Верблюд

1) (- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4),  (- 3; 4), (0; 7), (2; 4),  (4; 7), (7; 4), (9; 3), (9; 1), (8; - 1), (8; 1), (7; 1), (7; - 7), (6; - 7), (6; - 2), (4; - 1), (- 5; - 1),  (- 5; - 7), (- 6; - 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).

2) Око: (- 6; 7).

Кінь

1) (14; - 3), (6,5; 0), (4; 7), (2; 9), (3; 11), (3; 13), (0; 10), (- 2; 10), (- 8; 5,5), (- 8; 3),  (- 7; 2),  (- 5; 3),  (- 5; 4,5),  (0; 4),  (- 2; 0),  (- 2; - 3),   (- 5; - 1),  (- 7; - 2),  (- 5; - 10), (- 2; - 11), (- 2; - 8,5), (- 4; - 8), (- 4; - 4), (0; - 7,5), (3; - 5).

2) Око: (- 2; 7).

Верблюд

1) (- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4),  (- 3; 4), (0; 7), (2; 4),  (4; 7), (7; 4), (9; 3), (9; 1), (8; - 1), (8; 1), (7; 1), (7; - 7), (6; - 7), (6; - 2), (4; - 1), (- 5; - 1),  (- 5; - 7), (- 6; - 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).

2) Око: (- 6; 7).

Кінь

1) (14; - 3), (6,5; 0), (4; 7), (2; 9), (3; 11), (3; 13), (0; 10), (- 2; 10), (- 8; 5,5), (- 8; 3),  (- 7; 2),  (- 5; 3),  (- 5; 4,5),  (0; 4),  (- 2; 0),  (- 2; - 3),   (- 5; - 1),  (- 7; - 2),  (- 5; - 10), (- 2; - 11), (- 2; - 8,5), (- 4; - 8), (- 4; - 4), (0; - 7,5), (3; - 5).

2) Око: (- 2; 7).