Урок на тему "Слова близькі за значенням (синоніми). Практичне ознайомлення з фразеалогізмами, пояснення їх шляхом добору синонімів".

 

Зміст роботи

Вступ

Літературний огляд

Розділ 1. Особливості розвитку мислення молодших школярів.

 

Розділ 2. Формування логічного мислення у молодших школярів.

 

Розділ 3. Нестандартні логічні завдання – інструмент для розвитку логічного мислення.

 

Розділ 4. Розвиток логічного мислення у молодших школярів на уроках математики.

 

Висновки

Література

Додатки

• Цикл уроків з розвитку логічного мислення молодших школярів.
• Ігри та вправи, що розвивають логічне мислення.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вступ

        

                                  Все бачити, все зрозуміти, все пережити,

                                  Всі форми, всі кольори увібрати в себе очима,

                                  Пройти по всій землі палаючими ступнями,

                                  Все сприйняти і знову втілити.

                                                                 

                                                                           Максиміліан Волошин

 

   У  національній  доктрині   розвитку  освіти  України  в  XXI  столітті  чітко визначена головна  мета   української  системи освіти – створити умови     для розвитку кожної особистості як громадянина України, сформувати у дітей на-вички  самостійного наукового пізнання.   Сучасний рівень розвитку суспіль-ства,  відомості,  почерпнуті з різних інформаційних джерел, викликають по-требу вже у молодших школярів розкрити причини та суть явищ,   пояснити їх, тобто відверто мислити.

   В. Сухомлинський писав: «Розумна, одухотворена думкою і подивом   праця – це та глибина, на якій тримається човен думки».  Він рекомендував учителям  вчити  учня  аналізувати свої  думки, а   також   вивчати  мислительну діяльність учня, щоб правильно оперувати нею.

   В своїй роботі я виклала основні аспекти мислительної        діяльності учня, щоб  вчителі  могли  з ними добре  ознайомитися  і  використовувати  у своїй практиці.

   Відомо,  що діти  від  природи   допитливі і повні бажання вчитися. Але для того, щоб  кожна   дитина могла   розвинути свої творчі   здібності, необхідне розумне керівництво вчителя. Нерідко я спостерігаю, як учні, успішно навча-ючись в початковій школі, починають відставати в середніх і старших класах. Чому це   так відбувається? Я думаю,   що однією з причин є недостатній роз-виток уміння працювати самостійно, уміння вирішувати задачі творчо, знахо-дити раціональні шляхи рішення. На   те, що вчитель повинен розвивати логі-чне мислення учнів, вказується в методичній літературі, в пояснювальних за-писках до учбових програм. Проте вчитель не завжди знає як це робити. І то-му рівень логічної культури школярів на  сьогоднішній день не можна назва-ти задовільним. У практиці навчання   молодших школярів небезпечним є за-хоплення виконання дій по готовому зразку. Тут дитині не треба думати, ана-лізувати, зіставляти, - подивись, зрозумів, виконуй! В цьому    випадку ні про яку творчість і розум не йдеться. Це    механічне    запам’ятовування.    Буває

 учням пропонують завдання тільки тренувального характеру, дається   певна кількість   одноманітних   завдань. Учень   виконує   їх,але при  цьому у дітей затримується розвиток пізнавальної активності мислення.

   Отже     мета     моєї    роботи   розкрити шляхи вдосконалення пізнавальної активності    молодших     школярів,   подати вчителям необхідну інформацію щодо підбору нестандартних завдань на уроки. Це дасть можливість сформувати і розвинути всю різноманітність інтелектуальної і творчої        діяльності учнів,   забезпечити   перехід  від репродуктивних формально-логічних дій до творчих.

   Я вважаю, що одним з  найважливіших завдань, що стоїть перед    вчителем початкових класів, є розвиток самостійної логіки мислення,    яка дозволила б дітям будувати   висновки, приводити   докази, вислови, логічно зв’язані  між собою, робити висновки, обгрунтовувати свою думку. Дитина не може   бути щасливою, якщо в школі їй погано, нудно, якщо вона почувається     недоста-тньо здібною, щоб опанувати шкільну науку. Зробити    дитину    щасливою – основа моєї педагогічної діяльності.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 1.  ОСОБЛИВОСТІ МИСЛЕННЯ МОЛОДШИХ ШКОЛЯРІВ

   Як указує тлумачний словник С. І.Ожегова мислення – це здатність людини міркувати,  що є процесом віддзеркалення об’єктивної дійсності в уявленнях, думках, поняттях. Воно відображає реальність не тільки  у  вигляді   окремих предметів, явищ  та  їх  властивостей, а й  у визначенні зв’язків між ними, які  людиною безпосередньо не сприймаються. На практиці мислення як окремий психічний процес не  існує, він  присутній  у всіх інших пізнавальних  процесах: у сприйнятті, увазі, уяві, пам’яті, мовленні. І ці процеси цілком доступні дітям молодшого шкільного віку.   Педагогічні    дослідження показали, що в цей період головне значення набуває подальший розвиток мислення.  Причому мислення дитини молодшого   шкільного віку знаходиться  на  важливому етапі розвитку. Гармонійний інтелектуальний розвиток дитини в молодшому шкільному віці забезпечується, з одного боку, формуванням  мовлення,  його активним використанням у розв’язуванні   різноманітних  задач, а з  іншого – розвитку практичних дій, умінь оперувати   образами, поняттями,  абстракціями.

   З  метою  адаптації  мислення  молодших  школярів до   потрібного  темпу роботи, а також для   підвищення швидкості   реакції та гнучкості мислення, перед проведенням вправ проводжу короткочасну інтелектуальну  «розминку». Вона включає в себе довільні актуальні запитання. Наприклад:

- Яке сьогодні число?

- День тижня?

- Місяць?

- Як називається столиця України? Обласний центр?

- Швидко назвати сім імен хлопчиків ( дівчаток).

- Скільки кінців у двох палиць? Удвох з половиною?

- Стоять дві овечки. Одна дивиться на південь, друга – на північ. Чи бачать                                    вони одна одну? Чому?

   Залежно від того, якою мірою розумовий процес опирається на сприйняття, уявлення   чи   поняття,   розрізняють   три основні види мислення молодших школярів:

а)  наочно-дійове;

б) наочно-образне;

в) абстрактне ( словесно-логічне).

  а) Наочно-дійове мислення – мислення, пов’язане з практичними,   безпосе-редніми діями з предметами. Так, при вивченні теми «Довжина.  Порівняння довжини відрізків» (1 клас), діти,   користуючись міркою, визначають,   який відрізок довший, який коротший. При вивченні теми «Число і цифра 5. Утво-рення числа 5» діти за допомогою лічильних паличок утворюють число 5 ви-кладанням 4 паличок і додаванням ще однієї.

   б) Наочно – образне мислення – мислення,  яке  опирається на   сприйняття. Воно дає можливість вирішувати завдання в безпосередньо-даному наочному

 полі. На початку  періоду  молодшого шкільного віку домінуючим є   наочно-образне мислення, тому, якщо в перші два роки навчання діти багато працю-ють з візуальними зразками, то в наступних класах обсяг такого роду  занять скорочується. У міру оволодіння навчальною діяльністю і засвоєнням  основ наукових знань, школяр поступово залучається до системи наукових  понять, його розумові операції стають менш пов’язаними з конкретною  практичною діяльністю або наочною опорою. І все-таки образне мислення – основний вид мислення дітей 5 – 7 річного віку. Вже в цьому віці за допомогою спеціального тренування діти можуть оволодіти багатьма уміннями, пов’язаними з   цим видом мислення, подумки перетворювати образи реальних  предметів,   буду-вати наочні моделі, які відображають суттєві властивості об’єктів або явищ, планувати свої дії подумки.

 

             Ігри для тренування образного мислення ( Див. додаток № 1)

 

Здібності	Розвиваючі ігри
Перетворення образу          подумки	«Ломиголовки з паличками»
Орієнтація в просторі за           схемою	«Де сидить папуга?» « Накресли план-схему»
Читання і створення    схеми об’єкту	«Сузір’я”, «Прогноз погоди», «Збери за схемою», «Зашифруй казку»
Планування дій подумки	«Знайди всі стежинки»,»Гра в переставляння», «Шахова дошка», «Ломиголовка з паличками»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 2. ФОРМУВАННЯ ЛОГІЧНОГО МИСЛЕННЯ У МОЛОДШИХ ШКОЛЯРІВ

    У словнику психологічних понять К. К. Платонова логічне  мислення визначають як «вид мислення, суть якого полягає в орієнтуванні поняттями, судженнями і умовиводами з використанням законів логіки».

     Формування логічного мислення молодших школярів – важлива складова частина педагогічного процесу. Допомогти  учню в повній мірі проявити свої здібності, розвинути ініціативу, самостійність, творчий потенціал – одне з основних завдань сучасної школи. Логічне мислення формується на основі наочно-образного і є вищою стадією розвитку мислення взагалі. Процес досягнення цієї стадії доволі тривалий і складний. Пояснюється це тим, що повноцінний розвиток логічного мислення вимагає не лише високих результатів діяльності, але й передбачає наявність у дитини певної суми знань про спільні та суттєві ознаки предметів та явищ навколишнього світу. Тому і починатися він повинен з перших років навчання дитини в школі.

       На мою думку заняття з логічного мислення повинні бути направлені на формування передумов оволодіння дитиною системи наукових понять, які ставлять своєю метою розвиток у дитини логічних операцій: аналізу, синтезу, порівняння, узагальнення та класифікації. З  цією метою у своїй діяльності я стараюся щоб:

- усі уроки опиралися на здійснення індивідуального підходу до учнів;

- роблю необхідний підбір завдань, що більш ефективно впливають на розумову діяльність дитини;

- для досягнення вищих показників розвитку мислення молодших школярів впливають на учнів через індивідуальну оцінку діяльності;

- виявляю в класі найбільш розумово обдарованих дітей.

        На уроках розвиваю пізнавальні здібності логічного мислення молодших школярів за такою схемою : (Див. дод. №2)

 

Логічне мислення

 

 

пам'ять                                        уява сприйняття                                 мислення

 

         Великі вимоги щодо інтелектуального розвитку учнів стоять перед учителями початкових класів. Відповідно до вимог програми середньої загальноосвітньої школи, вчитель початкових класів  має постійно виробляти в учнів такі уміння:

1 клас. Виділяти в предметах певні ознаки, зіставляти групи предметів за однією суттєвою ознакою, робити з допомогою вчителя висновок – узагальнення. Та якості. Встановлювати схожість і відмінність між  кількома предметами, групувати предмети за родовими ознаками.

2 клас. Виділяти  в предметах певні ознаки та якості. Встановлювати схожість і відмінність між кількома предметами, групувати предмети за родовими ознаками.

3 клас. Розрізняти серед виділених ознак об’єкта головні та другорядні, порівнювати конкретні об’єкти за різними ознаками; з допомогою вчителя робити висновок-узагальнення, встановлювати зв'язок між причиною і наслідком, добирати факти, які підтверджують висловлену думку або суперечать їй.

4 клас. Самостійно робити висновок з пояснення вчителя, застосовувати порівняння та аналогію, класифікувати і групувати, доводити правильність певного судження, знаходити і виправляти граматичні і стилістичні помилки.

       Але, щоб ці уміння і навички вироблялися на високому рівні, треба формувати у дітей такі прийоми логічного мислення як порівняння, узагальнення, класифікація, систематизація, і змістовне співвідношення.

Розглянемо їх докладніше.

1) Навчаючи процесу порівняння я намагаюсь, щоб дитина оволоділа такими вміннями :

а) виділяла ознаки об’єкта  на основі співставлення його з іншим об’єктом.

    Діти в цьому віці (5-7 років) виділяють не більше 2-3 різних властивостей. Щоб дитина змогла побачити різноманіття властивостей, вона повинна навчитися аналізувати предмет з різних боків, спів ставляти цей предмет з другим предметом, який має інші властивості. Для цього я спершу підбираю для порівняння такі предмети, властивості яких було б легко помітити і зрозуміти, наприклад, таке завдання «Що спільного між предметами в кожній групі?»

 - Даю додаткове завдання:

                                                                     «Придумай ще по одному предмету 

 для кожної групи».

 

 

 

    Після цього поступово показую дітям приховані властивості цих предметів і вчу називати їх (Див дод. №3).

б) вчу визначати спільні і відмінні ознаки порівнювальних об’єктів.

    На цьому етапі важливо навчити дитину не лише виділяти ознаки і властивості різноманітних предметів, а ще й визначати, яку з них є спільними для порівняння предметів, а за якими ці предмети відрізняються один від одного.

   Для цього спершу навчаю дитину вмінню проводити порівняльний аналіз виділених властивостей і знаходити у них відмінності. І лише після цього переходимо до спільних властивостей. При цьому важливо навчити дитину бачити спільні властивості я к двох предметів, так і кількох.

Цьому сприяють такі завдання « У кожному ряду викресли одну зайву фігуру».

 

    

 

 

 

   

 

в)  вчу  виділяти суттєві і несуттєві ознаки об’єкту. Наприклад, таке завдання «Дай точну характеристику поняттю «Газета» ( папір, фотографія, програма, телебачення, оголошення, інформація). Виділяємо спочатку всі ознаки поняття, а після цього найсуттєвіші, які є обов’язковими для цього поняття.

2) Класифікація – вміння подумки поділяти предмети на класи за їх найбільш суттєвими ознаками. Для проведення класифікації потрібно, щоб дитина вміла аналізувати матеріал, спів ставляти один з одним окремі його елементи, знаходити в них спільні ознаки, здійснювати на основі цього узагальнення, розподіляти предмети на групи на основі виділених  в них і відображених у слові (назви групи) спільних ознак.

         Таким чином проведення класифікації передбачає використання таких способів мислення,  як порівняння і узагальнення. ( Див. дод №3).

3) Узагальнення – це здатність подумки об’єднувати предмети і  явища за їх спільними і суттєвими ознаками.

Так, навчаючи дитину прийому узагальнення прошу її конкретизувати загальне поняття через окремі поняття « дай спільну назву кожній парі слів»:

• морква, помідор;
• штани, плаття і т.д.

При цьому вчу дітей групувати об’єкти на основі самостійно знайдених спільних ознак і позначити утворену групу словом. Цікаве завдання на етапі узагальнення: « Розподілити солова кожного рядка за їх значенням від часткового до найбільш загального». Слова :

    Також  на цьому етапі вчу дітей розподіляти об’єкти за класами. Завдання для уроку математики : «Кожне слово запиши у відповідний стовпчик».

      №1             №2       №3

Знаки дій Геометричні фігури     Числа

Довідка: квадрат, сім, додавання, сто, коло, трикутник, віднімання, ділення, нуль, прямокутник, двадцять.

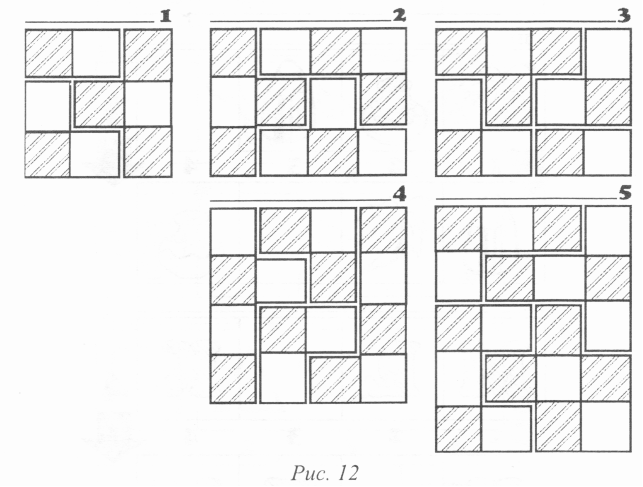
4) Систематизувати – означає приводити до системи, розміщувати об’єкти за певними ознаками, встановлювати певну послідовність. Вчу дітей знаходити закономірність розміщення об’єктів впорядковувати за однією ознакою і розташованих в одному ряді. Використовую такі завдання «Яку фігуру треба поставити замість знака питання?»

  

 ?

   В більш ускладнених завданнях вчу дітей знаходити закономірність  розташованих об’єктів, впорядкованих на основі двох чи більше ознак і розміщених в матриці.

 

?

 

    Починати такі завдання треба з простої матриці (2х2) і ознайомленням двох ознак: за формою, кольором; просторового розміщення об’єкта; додаванням або відніманням частин об’єкту, зміна кількості об’єктів ( Див дод. №3)

5) Коли дитина навчиться співвідносити, порівнювати предмети за їх зовнішніми ознаками(формою, кольором, величиною,тощо) переходжу до розвитку більш складної інтелектуальної дії – співвідношення предметів за змістом. Співвідносити предмети за змістом – означає знайти якість зв’язки між ними. Краще, якщо ці зв’язки базуються на суттєвих явищах, властивостях предметів і явищ. Проте важливо вчити дитину опираючись і на другорядні,  менш важливі  властивості й ознаки. Щоб знайти ці зв’язки вчу дітей порівнювати предмети між собою, звертаючи увагу на їх функції, призначення, інші внутрішні властивості чи ознаки. Порівнювані предмети можуть мати зв’язки, засновані на різних типах відношень. Наприклад, це можуть бути зв’язки, засновані на відношеннях типу «частина – ціле» (колесо-машина, будинок-дах), на протилежності властивостей предметів чи явищ (сіль-цукор, день-ніч), на подібності чи приналежності до одного роду або виду ( ложка-виделка, яблуко-груша). Навчання «змістового співвідношення» - це навчання вмінню швидко знаходити такі відношення.  Впроваджую таку послідовність навчання:

а) змістове співвідношення двох наочно представлених предметів («картинка - картинка»);

б) співвідношення наочно представленого предмета з предметом, позначеним словом («картинка-слово»).

в) змістове співвідношення предметів та явищ, представлених у вигляді слів («слово – слово») слово може позначати якийсь предмет, його окрему властивість, явище природи і багато іншого. Спершу пропоную завдання, в яких дитині за двома заданими словами потрібно знайти змістовний зв'язок між конкретними предметами. Пізніше  для співставлення пропоную більш абстрактні поняття, які позначають властивості предметів, природних явищ і т.д. Важливо, щоб ці поняття були знайомі дитині.

     Всі цікаві види завдань для формування способів логічного мислення пропоную  додатках. Як видно всі прийоми логічного мислення взаємозалежні і їхнє повноцінне формування можливо тільки в комплексі.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Розділ 3.  НЕСТАНДАРТНІ ЛОГІЧНІ ЗАВДАННЯ – ІНСТРУМЕНТ ДЛЯ РОЗВИТКУ ЛОГІЧНОГО МИСЛЕННЯ.

Основними формами логічного мислення  є поняття, судження, умовиводи.             Індивідуальні відмінності в діяльності мислення усне можуть проявлятися в таких якостях мислення: широта, глибина і самостійність мислення, гнучкість думки, швидкість та практичність розуму.

   Як показує мій досвід у шкільному віці одним х ефективних способів розвитку мислення є рішення школярами нестандартних завдань. Значне місце питанню навчання молодших  школярів нестандартним завдань приділяв в своїх роботах найвідоміший вітчизняний педагог В.О. Сухом-линський, суть його міркування зводиться до вивчення та аналізу процесу вирішення дітьми логічних завдань, при цьому він практичним шляхом виявляв особливості мислення молодших школярів.

    Процес розв’язування будь-якого завдання з логічним навантаженням містить ряд етапів.

Складові процесу розв’язування завдань

З логічним навантаженням

Етапи розмірковування	Уміння	Операційний склад умінь
Підготовчий	1)Аналізувати структуру завдань 2)Зіставляти дане завдання з відомими завданнями.	- виділяти умову і запит; - виділення складових умови і вимоги; - підведення завдання під певний тип, якщо такий має місце; - виявлення схожих завдань.
Визрівання нової ідеї, формування гіпотез (передбачення)	Знаходити приховані зв’язки між даними і невідомими елементами	- розпізнавання даних елементів у різних (у тому числі і нових) поєднаннях; - застосування теоретичних положень, які стосуються елементів завдання; - виявлення можливості використання результату чи ідеї розв’язання спорідненої задачі.
Перевірка гіпотез	Аналізувати гіпотезу щодо можливого розв’язання завдання	- перевірка правильності гіпотези (чи не виникає суперечності з умовою завдання); - доведення висуненої гіпотези.
Розвиток ідеї	Логічно опрацьовувати знайдене розв’язання завдання.	- критичне опрацювання знайденого розв’язання з різних позицій (правильності, економіч-ності, естетичності); - узагальнення результатів розв’язування завдання виведення певної закономірності; - узгодження інформації, щодо застосування ідеї, прийомів, способів з  попередніми знаннями  вміннями; - встановлення зв’язку даного завдання з життєвими ситуаціями.

 

Розглянемо всі складові процесу розв’язування завдань з логічним навантаженням.

    Так  у 1 класі при вивченні теми « Властивості  та  відношення предметів. Порівняння кількості предметів.» на підготовчому етапі використовую завдання,  в яких зв'язок між поняттями передано за допомогою відношень, «більш-менш»; «старий – молодий»; «ближчу - далі». В результаті учні мають усвідомити, що відношення 2більш – менше» ми вживаємо, порівнюючи кількість предметів; поняття  «ближче - далі» - відстань; «вище – нижче» - висоту. Діти працюють з  такими твердженнями « Оксанці треба подолати до школи більшу відстань, ніж Маринці. Хто живе ближче до школи? Хто далі?» .  Демонструємо це схематично

школа                      Марина  Оксана

 

 

  

        На  другому етапі  пропоную задачі, в умові яких є тільки 2 групи предметів, або 2 діючі особи. Діти розв’язують задачі такого плану:

« Ганнуся живе ближче до школи ніж Галина, хто з них живе далі від школи?». Учні мають усвідомити, що за умовою задачі, є тільки 2 дівчинки – Ганна і Галина, і  те, що Ганна живе ближче до школи, ніж Галинка.

        На третьому етапі учні разом зі мною  міркують так: якщо Ганна живе ближче до школи, ніж Галинка, то Галинка живе далі від школи, порівняно з Ганною.

Після детального розбору задачі пропоную учням розв’язати аналогічні задачі (Див. дод. №4)

 Пізніше переходимо до розв’язування задач, в умові яких є три групи предметів або три діючі особи. Наприклад, пропоную учням розв’язати таку задачу: « У Лариси вдома ляльок більше, ніж у Катрусі, у Вікторії ляльок більше, ніж у Лариси. У кого з дівчаток ляльок найбільше, а у кого найменше?». Тут є ефективною графічна ілюстрація умови задачі. Вона має такий вигляд:

 

 

 

 Л               К  В 

Після цього можна перейти до розбору задачі, в умові якої є чотири групи предметів, або чотири діючі особи. Наприклад , можна запропонувати учням розв’язати таку задачу: « Катя вища на зріст від Люди, Валя вища від Зої, а Зоя від Каті. Хто з цих дівчаток найвищий?». Важливо, щоб на цьому етапі учні усвідомили, що дітей четверо і тому відрізків, які схематично ілюструють їх зріст, також має бути чотири. Перші два відрізки, які ілюструють зріст Каті і Люди учні креслять правильно, бо вже мають досвід розв’язання подібних задач. Далі в умові задачі – інформація про Валю і Зою – інших двох дівчат. На цьому етапі рекомендую дітям відрізок, який схематично ілюструє зріст Валі креслити довільно. Наступний відрізок, яких схематично ілюструє зріст Зої ми креслимо меншим, ніж попередній відрізок, бо за умовою Валя вище від Зої. Задаю дітям питання :

• Як проілюструвати інформацію – Зоя вища від Каті? (Учням важко відповісти на це запитання)
• Знайдіть відрізок,  який зображує зріст Каті (1 відрізок)
• Що відомо про зріст Зої? (Зоя вища від Каті)
• Чи правильно накреслили відрізок, який зображує зріст Зої?

Тепер графічна ілюстрація умови матиме такий вигляд:

 

 

 

 

       К               Л В    З

Після того як учні правильно виконали графічну ілюстрацію задачі, вони дають правильну відповідь на запитання задачі : Валя найвища з дівчат. Пропоную дітям розташувати дівчат за зростом від найвищої до найнижчої.

        У  другому  класі знайомлю дітей зі словом «поняття» - це думка, висловлена словом, яке відповідає на питання хто? Що?.  Пояснюю, що поняття бувають родові і видові. Родові – назва певної групи предметів, а назва кожного предмета з цієї групи – видове поняття.  Наприклад,  «многокутник» - родове поняття, а « трикутник, чотирикутник» тощо – видове. Пропоную дітям самостійно навести приклади родових і видових понять.

         Після цього пояснюю дітям, що кожне поняття має зміст і обсяг. Зміст поняття – всі ознаки, які в ньому містяться. Наприклад, зміст поняття «чотирикутник» такий : це геометр фігура, родове поняття – має 4 сторони, 4 кута, 4 вершини.

Об’єм поняття – це ті предмети, які ми уявляємо, коли називаємо дане поняття. Коли називаємо поняття, чотирикутник; то уявляємо і прямокутник, і квадрат – це  обсяг поняття «чотирикутник».

 

 

 

 

 

Далі знайомлю з видами понять:

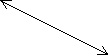
видове одиничне

 

       Поняття

 

родове   конкретне абстрактне

 

  Хочу  запропонувати фрагмент уроку математики вивчення математичного поняття «трикутник».

Заздалегідь креслю на дошці трикутник, чотирикутник, п’ятикутник, шестикутник. Даю дітям установку: дати визначення трикутника.

За таким планом:

• сформулювати ознаки відмінності;
• сформулювати ознаки схожості фігур (родове поняття);
•  сформулювати визначення поняття «трикутник».

Деякі діти дають таке визначення: « Трикутник має 3 групи, з сторони». Вчитель. Як ви вважаєте, чи правильне та повне було дано визначення?

 Частина учнів вважає, що визначення – повне, деякі – відповідь  правильна, але неповна. Аналізуючи неправильну відповідь я вказую на помилку – не було сформульована ознака схожості між зображеними на дошці фігурами. Після цього один учень пропонує правильне визначення: « Трикутник – це геометрична фігура, яка має 3 сторони, 3 кута і 3 вершини.

        У третьому класі  знайомлю дітей із змістом поняття «судження». Судження – думка висловлена розповідним реченням,  у якій щось стверджується, або заперечується про предмет дійсності, про їх ознаки, дії, взаємозв’язки. Наприклад судження : «Сума чисел шість і чотири дорівнює десяти». Це судження істинне (відповідає дійсності), але судження : «Сума чисел шість і чотири не дорівнює десяти» - хибне (не відповідає дійсності). Вчу дітей перетворювати істинні судження на хибні і навпаки за допомогою частки не. На уроках вводимо в свої судження слова: всі, деякі, жодний, принаймні один. Метою застосування зазначених завдань є розвиток математичного мовлення молодших школярів, вміння чітко висловлювати власну думку.

      Так на уроці пропоную дітям перевірити, чи правильно розв’язано приклади на дошці та скласти істинне і хибне судження.

2 + 3 = 5 6 + 4 = 9

9 – 4 = 6 7 – 5 = 2

Учні складають такі судження: « Сім мінус п’ять дорівнює два» - істинне і « різниця чисел дев’ять і чотири дорівнює шість» - хибне. Пропоную перетворити хибне судження на істинне за допомогою частина не. « Різниця чисел дев’ять і чотири не дорівнює шести.» (це не нове судження, а його перетворення). Після цього вчу вводити в свої судження слова: всі, будь-який, кожний, деякі, жодний (після розкриття змісту цих слів). Пропоную зробити висновок про правильність розв’язання прикладів на дошці. Учні складають такі судження: «Деякі приклади розв’язані  правильно», « принаймні один приклад розв’язаний правильно».

       З метою закріплення певних знань з математики та розвитку математичного мовлення пропоную учням такі завдання:

Прочитай число 13, 7, 20, 54,1,44 знайдіть серед поданих суджень істине:

• Всі числа – двоцифрові
• Деякі числа – двоцифрові
• Жодне число не є двоцифровим.

Більше розглянути у додатку №5.

 

4 клас – узагальнення і систематизація вивченого на уроках математики

за курс початкової школи, тут пропонується учням завдання з логічним навантаженням, які були вивчені у 1 – 3 класах. Але у 4 класі є і нове знайомство зі складними судженнями,  які містять сполучники і, чи. Судження: «Число12 – двоцифрове» - просте, а судження: «Число 12 – двоцифрове і парне» - складне. Складне судження – судження, яке складається з двох чи більше простих суджень. Знайомлю дітей, що істинність чи хибність складного судження залежить від істинності чи хибності його частин – простих суджень. Якщо хоч одна частина складного судження хибна, то все складне судження хибне. Так судження: «Число 12 – двоцифрове і парне»  - істинне, бо обидві його частини – істинні прості судження. Далі вчу перетворювати хибні складні судження на істинні за допомогою сполучника чи (або). Наприклад, судження: « Число 2045 ділиться на 2 і на 5» - хибне, бо перша частина його хибне просте судження, а друга істинне. Якщо замінити сполучник і на сполучник чи, то дане судження стане істинним. До речі, хибність першої частини учні встановлюють не виконуючи обчислень, а на основі знань про парні і не парні числа, а істинність другої частини за ознакою подільності на 5.

Дуже  цікаве завдання з геометричними фігурами:

 

 

         

 

          Завдання вчителя дітям: скласти по одному істинному і хибному судженню із сполучниками і, чи.

Діти складають такі судження:

• На малюнку є трикутник і прямокутник (істинне).
• На малюнку є трикутник і лялька (хибне0
• На малюнку зображені 2 прямокутника чи один трикутник (істине)
• На малюнку зображені леви та тигри (хибне).

Які нестандартні завдання я використовую у своїй роботі?

                         творчі завдання                                    ребуси

 

математичні загадки цікаві квадрати

Нестандартні завдання

 

         віршовані задачі ігрові вправи

прислів’я і приказки

 

 

 

Розділ 4. РОЗВИТОК ЛОГІЧНОГО МИСЛЕННЯ У МОЛОДШИХ ШКОЛЯРІВ НА УРОКАХ МАТЕМАТИКИ.

         Мислення дитини в тій чи іншій мірі розвиває кожен загальноосвітній предмет, що викладається в початковій школі. Однак математика займає особливе місце. « Головна задача навчання математиці, причому із самого початку, з першого класу – учити міркувати, учити мислити», - пискав педагог – новатор А. А. Столяр.

          Сьогодні  математика, як жива наука з багато бічними зв’язками, робить звичайний вплив на розвиток інших наук і практик, також є базою науково-технічного прогресу і важливим компонентом розвитку особи. Однією з основних цілей вивчення математики є формування і розвиток мислення дитини, в першу чергу абстрактного мислення. Її абстрактний характер і спільність методів, які широко використовуються в різних областях, найбільшою мірою спирають оволодіння учнями елементів логіки, грамотності, вмінню застосовувати на уроках математики загально логічні поняття, прийоми і способи дії при вивченні інших предметів.

         Я з’ясувала, що  успішне формування логічного мислення молодших школярів на  у роках математики дає позитивний результат, якщо вчитель:

• для роботи на уроці відводить 5-7 хвилин на розв’язання задач з логічним навантаженням;
• використовує задачі з логічним навантаженням під час опрацювання відповідного програмного матеріалу;
•  враховує об’єктивні труднощі задач та математичну підготовку учнів певного касу;
• розвиває умови задач емоційно, спираючись на наочність;
• надає учням змогу поміркувати, обмінятися думками, запропонувати різні варіанти розв’язання;
•  намагається поступово залучити до розв’язання задач найбільшу кількість дітей;
• пропонує добірку таких задач для домашньої роботи;
• стимулює самостійне створення текстів задач;
•  проводить додаткову позакласну роботу з учнями,  які проявляють особливий інтерес до математики.

          Логічне мислення молодших школярів ґрунтується  на рішенні не стандартних завдань, їх єдності навчання, виховання і розвитку. Рішення цих завдань  здатно прищепити інтерес дитини до вивчення, класичної математики.

На мою думку вчитель на кожен урок повинен пропонувати своїм

вихованцям що-не-будь неординарне, цікаве, « примусити» дітей розмірковувати. Поділюся методикою роботи над задачами з логічним навантаженням.

         Задачі нового типу починаю розв’язувати з найпростіших, доступних усім учням. Якщо на кожному уроці  усно розв’язувати 4-5 таких задач, модна досягти гарних результатів. Роль простих задач надзвичайно велика. Вона  є основним засобом з формування поняття про арифметичні  дії та величини. У процесі розв’язання простих задач учні опановують основні прийоми роботи над задачею.  Високий рівень умінь розв’язувати прості задачі -  необхідна умова успішного розвитку вмінь розв’язувати задачі складні. Зразки простих задач у додатку №6.

         В. Сухомлинський значне місце відводив навчанню школярів розв’язувати задачі. У книжці « Серце віддаю дітям» він писав: « У навколишньому світі тисячі задач. Їх придумав народ, вони живуть у народній творчості. Як розповіді-загадки. Щоб розв’язати задачу треба мислити абстрактними поняттями, відволікаючись від конкретного».

         Як же досягти найбільших результатів у роботі над задачею? На мою думку це:

1. Робота над віршованими задачами. Це шлях до вироблення твердих знань з математики.
2.  Рішення задач різними способами. Звичка знаходити інший спосіб рішення грає велику роль у майбутньому.
3. Правильно організований спосіб аналізу задачі – від питання чи від даних до питання.
4. Уявлення ситуацій, описаних в задачі (намалювати, картинку). Розбиваємо текст задачі на значеннєві частини, моделюємо ситуацію за допомогою креслення.
5. Самостійне складання задачі учнями: -
6. Рішення задач з відсутніми чи зайвими даними.
7. Зміна питання задачі.
8. Складання різних виразів за даними задачі і їх пояснення. Вибирати       той вираз, що є відповіддю на питання задачі.
9. Пояснення готового рішення задачі.

10) Запис двох  рішень на дошці: одного вірного й іншого невірного.

 11)  Зміна умови задачі так, щоб вона розв’язувалася іншою дією.

 12)  Складання аналогічної задачі зі зміненими даними.

 13)  Рішення оберненої задачі.

     

        Розглянемо усі види роботи над задачею з підручника « Математика» 3 клас  (автор М. В. Богданович)

Задача №502

   У господарстві було 24 трактора, комбайнів – у 3 рази менше, автомобілів – у 4 рази менше, ніж комбайнів. ( Задача без питання)

1. Аналіз задачі:

Про що йде мова в задачі?

Що означає кожне число?

Що означає у менше?

Яке питання можна поставити до задачі? ( скільки автомобілів у господарстві).

2. Складаємо план розв’язання задачі:

• Що сказано про кількість тракторів?
• Що відомо про кількість комбайнів?
• Про що можна дізнатися по цим двом числам? ( Скільки комбайнів у господарстві)

 

1.                       :                      

 

 

 

 

• Що сказано в задачі про кількість автомобілів? (Їх у 4 р.<, ніж тракторів)
• Знаючи кількість тракторів, чи можливо дізнатися кількість автомобілів?

2.  

 :   

 

 

 

• Чи дамо відповідь на ваше запитання до задачі? (Так)

 

 1) 

 :   

 

 

 2) :

 

 

 

 

3)  Після детального аналізу задачі і її розв’язання працюємо на таким завданням. Про що дізнаємося, коли знайдемо значення виразів:

24: 3 24 – 24 : 3 24 + 24 : 3+24 : 3

 24 : 3 : 4

4)  Пропоную змінити умову задачі, щоб вона розв’язувалась діями : і ·. Задача. У господарстві було 24 трактора, комбайнів – у 3 рази менше, автомобілів – у 4 рази більше, ніж комбайнів.

5)  Складаємо аналогічну задачу до даної зі зміною даних в умові. Задача. У господарстві було 48 тракторів, комбайнів – у 6 разів менше, автомобілів – у 2 рази менше, ніж комбайнів. Скільки автомобілів у господарстві?

6)  Пропоную скласти обернену задачу до основної задачі. Задача. У господарстві було 8 комбайнів, тракторів у 3 рази більше, ніж комбайнів, а автомобілів – у 4 рази менше, ніж комбайнів. Скільки тракторів було у господарстві?

7) Пропоную у запропонованій задачі в підручнику змінити запитання. Задача. У господарстві було 24 трактори, комбайнів у 3 рази менше, автомобілів – у 4 рази менше, ніж комбайнів. Скільки всього машин було у господарстві?

8)  Далі пропоную дітям розв’язати  задачу аналогічну до  даної.

      Отже, розвиваючий ефект задач та інших творчих завдань розширює математичний кругозір молодших школярів, дозволяє активніше використовувати математичні знання в повсякденному житті, сприяє розвитку важливої здатності людського розуму – передбачати результати не тільки здійснювати дій, а й тих, що плануються. Це стосується і в цілому уроків математики.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок

 

      Актуальність моїх досліджень по даній темі: « Формування і розвиток логічного мислення молодших школярів» полягає в тому, що в наш час існує необхідність нового типу освітнього результату, орієнтованого на вирішення реальних життєвих завдання. В умовах постійно зростаючого обсягу інформації, навчального матеріалу, що його має засвоїти дитина, виникає загальна потреба шукати шляхи ефективного навчання, приховані резерви розумової активності, підвищення самостійності у пізнання навколишнього  світу, методи і прийоми якісного засвоєння дітьми знань, умінь і навичок у різних видах діяльності.

       З власної практики оптимальними шляхами досягнення цієї мети є:

• добір доцільних методів і прийомів, спрямованих на активне сприймання навчального матеріалу;
• інтегрування отриманої інформації з попередніми знаннями і досвідом учнів;
•  забезпечення умов для активної діяльності учнів з урахуванням їх індивідуальних особливостей, здібностей, інтересів;
• формування у дітей раціональних прийомів мислення;
• створення умов для використання на уроці інформації, здобутої поза школою;
• передбачення вчителем певних інтелектуальних труднощів при оволодінні дітьми навчальним матеріалом;
• активізація пізнавальної діяльності учнів з використанням проблемно-пошукових методів;
•  формування у дітей вміння вчитися, поповнювати обсяг своїх знань.

      Внаслідок цього у дітей формується цілісна система сприйняття навколишнього світу, активізується мислення, а отже розвиваються і вдосконалюються пізнавальні інтереси, що позитивно в пливає на оволодіння дітьми навчального матеріалу. Аналізуючи якість знань з математики у своєму класі, я можу сказати, що 81% учнів успішно оволодівають програмовим матеріалом з цього предмету, 20% учнів класу беруть участь з  шкільних та міських олімпіадах і показують хороші результати.

Аналізуючи показники класу3 з вивчення української мови, хочу відмітити, що більшість учнів засвоює програму на достатньому рівні. А учениця класу Руссу А.  у 2012 році зайняла ΙΙΙ призове місце в обласному етапі XIII мінародного конкурсу з української мови імені Петра Яцика. Але на цьому я не збираюсь зупинятися.

Література

1. Навчальні програми для загальноосвітніх навчальних закладів із навчанням українською мовою 1 – 4 класи: Видавничий дім «Освіта», 2012 – 138с.

2. Митник О. Логіка на уроках математики (методика роботи над завданнями з логічним навантаженням) Київ: Початкова школа, 2004 – с.15 – 67.

3. Барташнікова І.А., Барташніков О.О. « Розвиток наочно-образного та логічного мислення у дітей 5-7 років», Тернопіль: Богдан, 1998 с. 8-41.

4. Чекіна О. Ю. Задачі  з логічним навантаженням на уроках математики в початковій школі.  «Початкове навчання» №26, 2010 – 45 с.

5. Гісь О. Планета міркувань. Навчальний посібник з розвитку мислення. Київ: ТОВ «Інститут сучасного підручника», 2013 – с. 100 – 150.

6. Стеценко І. Логіки світу. Початкова освіта №47. 2004 – 12с.

7. Народницький Є.Г. Еврика.  – Харків: Видавнича група «основа»; 2010 – с. 4-50 .

8. Митник О. Курс «Логіка» в системі загальної середньої освіти. Початкова школа №10. 2007, - с. 2 – 16.

9. Тихомирова Л.Ф. «Развитие логического мышленя детей». Академия развития, 2000. – с. 3- 18.

10. Барташнікова І.А., Барташніков О.О. Інтелектуальна ігротека (Тренування інтелектуальних творчих здібностей дітей 6 років): - Львів: “Оксарт”. - 1996.

11. Маланюк П.М.Стежки до математичних узагальнень. –  Тернопіль: Підручник і посібники, 1998.

 

 

 

 

ДОДАТКИ

Цикл уроків  з розвитку логічного мислення.

 Урок математики в 1 класі на тему: «Число і цифра 7. Написання цифри 7. Порівняння кількості предметів. Послідовність чисел у межах 7. Складання і обчислювання значень виразів.»

 

Вчитель початкових класів:

Андрущенко Валентина Миколаївна

Урок математики ( 1 клас).

Тема. Число і цифра 7. Написання цифри 7. Порівняння кількості предметів. Послідовність чисел у межах 7. Складання і обчислювання значень виразів.

Мета:

• дидактична: ознайомити з числом і цифрою 7, вчити писати цифру 7; продовжувати роботу над формуванням навички порівняння чисел в межах 7. Вчити складати, читати і записувати приклади;
• розвиваюча:  розвивати увагу, спостереження, логічне мислення, вміння оцінювати спосіб виконання завдання;
• виховна: виховувати інтерес та позитивне ставлення до предмету, самостійність та ініціативу.

Тип уроку: урок засвоєння нових знань.

Форма уроку: урок-казка.

Обладнання: підручник з математики (1клас Ф.М. Рівкінд); зошит з друкованою основою; зразок написання цифри 7; картки з розрізаними цифрами; лічильні палички, ілюстрації казкових героїв.

Епіграф уроку:

Математику тому вивчати треба,

що вона розум упорядковує.

Хід уроку

Ι. Організаційна частина. Привітання.

Учитель. – Добрий день! В добрий час!

  Рада, діти, бачить вас!

  Ви почули всі дзвінок?

  Він покликав на урок.

  Тож і ми часу не гаєм

  До роботи приступаєм.

Девіз нашого уроку:

 Міркуємо – швидко,

 відповідаємо – точно,

 рахуємо – вірно,

 пишемо – гарно.

ΙΙ. Актуалізація опорних знань учнів.

1. Інтерактивна вправа «Мозковий штурм»

Учитель. – Як  ви думаєте, навіщо ми вивчаємо такий предмет, як математика?

Діти. – Щоб  добре рахувати, розв’язувати задачі.

Учитель. – Де  ми застосовуємо знання, роботі на уроках математики?

Діти. – В  життєвих ситуаціях.

2. План уроку

• Знаю
• Здобуду нові знання
• Застосовую
• Підсумки

ΙΙΙ. Повідомлення теми та завдань уроку.

Учитель. – Виходячи  з плану, будемо вивчати нову тему. Щоб ви хотіли дізнатися по цій темі?

Тема нашого уроку: «Число і цифра 7. Утворення числа 7.»

3. «Дерево знань».

Учитель. – Які  теми вивчали на попередніх уроках? Що треба нам сьогодні повторити?

4. Задачі уроку

Учитель. – Про  які якості треба пам’ятати, щоб урок пройшов не марно, щоб досягти мети?

Діти. – Бути  уважними, швидко рахувати.

Учитель. – Які особисті завдання ставите перед собою, приходячи на урок математики? Побудуйте твердження: «Я перед собою ставлю завдання …».

IV. Повторення вивченого матеріалу.

1) Учитель. – До нас в гості завітала казка. Як звати героїню? (Білосніжка)

2) інтерактивна вправа « Рефлексія». Які емоції і почуття викликає образ нашої героїні? (Позитивні, хороші).

3)Усний рахунок.

Гра «Знайди доріжку до дому семи гномів».

 

 

 

 6 – 3

 2 + 3

4 – 1     

1 + 5

 

 

 

 

 

 

4) Каліграфічна хвилинка (з елементами логіки).

Учитель. – Гноми  вчили цифри, а зла чарівниця вирішила їм перешкодити. Вона розрізала кожну картку на 2 частини. Допоможіть гномам поєднати картки з цифрами.

 

                                                                               

 

Давайте каліграфічно правильно пропишемо ці цифри у зошиті.

V. Формування знань, умінь, навичок.

1) Утворення числа 7.

Учитель. – Скільки  гномів стоїть біля будинку?(6)

А скільки їх було у казці? (7)

Що треба зробити, щоб їх стало 7?

Як же утворити число 7? (6 + 1 =7)

Яке число є попереднім до числа 7?

На скільки воно менше від 7?

Діти. – 7  кольорів веселки; казка «Семеро козенят», 7 чудес світу; 7 днів у тижні, тощо.

2) Ознайомлення з цифрою 7.

Учитель. – На  що схожа цифра 7?

Цифра 7 , як кочерга,

В неї, бач, одна нога.

3) Написання цифри 7 .

- написання і пояснення вчителем;

- написання цифри мокрим пензлем;

- написання в повітрі;

- написання в зошиті.

4) Робота в підручнику (с. 33, завдання 1)

Учитель. – Кого  бачите на малюнку?

Діти. – Тварин.

Учитель. – Скільки тварин справа? (6)

                 Хто до них приєднався?

 Скільки тварин стало?

 Як утворили число7.

Фізхвилинка

Раз – підняти руки вгору,

Два –нагнутися додолу,

Не згинайте, діти, ноги,

Як торкаєтесь підлоги,

Три, чотири – прямо стати,

Будем знову починати.

Хто зуміє присідати

І ногам роботу дати?

Раз – піднялись, два – присіли,

Хай мужніє наше тіло.

Хто втомився присідати,

Може вже відпочивати.

Руки в боки, руки так,

Руки вгору, як вітряк.

 

VI. Закріплення  вивченого матеріалу.

1) Логічна вправа «Узагальнення».

Учитель. – Відгадайте  по даним словам, де знаходяться гноми і Білосніжка (дерева, земля, повітря, дикі тварини). Яке це поняття? (Збірне).

2) Робота в підручнику (завдання 2).

Складання нерівностей.

Учитель. – Хто зображений на малюнку?

     Утворіть множини? (Метелики, квіти).

    Скільки елементів у кожній множині?

    Якими числами позначимо кількість елементів?

                    Порівняйте числа і поставте порівняльні знаки.

3) Робота в зошиті з друкованою основою. (завдання 2). Робота в парах.

Учитель. – Розгляньте уважно малюнки (райдуга, квітка-семицвітка, гноми). Складіть твердження, що об’єднує всі ці малюнки.

Твердження: «Всі ці предмети об’єднує …»

4) Завдання з логіки «Обведи зайву фігуру» (завдання 3).

Учитель. – Які множини можна утворити?

Діти. – 1 множини – за кольором;

             2 множини – за розміром; 

             3 множини – за кількістю кутів, сторін, вершин.

Учитель. – Обведіть зайву фігуру.

 Докажіть, чому так?

5) Самостійне розв’язування прикладів (завдання 5). Перевірка правильності розв’язання сигнальними картками.

VIII. Робота з геометричним матеріалом.

Учитель. – Візьміть 7 паличок. Викладіть з них будинок, в якому жили герої казки. Які геометричні фігури використали? Чим вони відрізняються одна від одної?

IX. Підсумок уроку.

1) «Мікрофон».

- Що нового дізналися на уроці?

- З яких чисел утворюється число 7?

- Які числа > 7, < 7?

2) «Рефлексія».
- Чи сподобалося завдання казкових героїв?

 

 

 

 

 

 

Урок математики в 1 класі на тему: «Довжина. Вимірювання довжини відрізків. Сантиметр. Обчислення значень виразів».

 

Вчитель початкових класів:

Андрущенко Валентина Миколаївна

Урок математики (1 клас).

Тема. Довжина. Вимірювання довжини відрізків. Сантиметр. Обчислення значень виразів.

Мета:

• дидактична: ознайомити з поняттям «довжина», з мірою довжини сантиметром і сантиметровою лінійкою, учити вимірювати довжину відрізків, ознайомити учнів з різними мірками і різними одиницями  вимірювання;
• розвиваюча: розвивати логічне мислення, обчислювальні навички, увагу, спостережливість, вміння висловлювати свою думку;
•  виховна: виховувати старанність, організованість, працелюбність, самостійність.

Тип уроку: урок засвоєння нових знань.

Форми уроки: урок-казка.

Форми роботи: групова, індивідуальна, диференційована, парна.

Обладнання: ілюстрації до казки «Червона шапочка»; зображення стародавніх мір довжини; лінійки, олівці, кольорові смужки, зошити, підручники  (математика 1 клас, Ф. М. Рівкінд); геометричний матеріал.

Хід уроку

I. Організація класу.

    Сьогодні у нас не звичайний урок

    У казку зробимо ще один крок,

    А з казкою ми зустрічалися не раз

    І знову вона завітає до нас.

В казках є завжди перешкоди, та знаю, що їх для кмітливих малят не буває.

Учитель. – До якого уроку підготувалися?

• Інтерактивна  вправа «Мозковий штурм»?
• Що робимо на уроках математики?

 

 

 

 

рахуємо                                        відповідаємо міркуємо

 

 вимірюємо Математика розв’язуємо

 граємо порівнюємо

 

• А навіщо вам вивчати такий предмет, як математика?
• Де ви застосовуєте знання, набуті на уроці?

Складіть твердження : « Математику треба вивчати тля того ,щоб …».

Обіцяєте бути: уважними, старанними, дисциплінованими, активними, щоб почути у кінці, що у вашому 1 клас діти просто – молодці.

ІІ. План уроку.

Учитель. – Уважно послухайте, що ми сьогодні будемо робити на уроці  дайте відповідь на моє запитання:

1. Знаю.
2. Здобуду нові знання.
3. Застосовую
4. Підсумую

• Чи будимо вивчати сьогодні нову тему?
• А допоможе нам в цьому героїня однієї казки. Хто це? (зображення червоної шапочки)

Загадка. Старенька бабуся у лісі жила.

                Гостинець для неї онучка несла.

                Та стрінувся в лісі їй сірий хижак.

 Цю дівчинку звати пригадайте як?

Учитель. – Чому їй дали таке цікаве ім’я ?

• Які  дійові особи  ще зустрічаються у казці?

Інтерактивна вправа «Рефлексія».

• Які виникають у вас почуття, коли уявляєте червону шапочку?
• А вовка?
• Написав цю чудову казку французький письменник Шарль Перро.        (портрет).

Вправа  «Асоціативний малюнок».

• Які казки цього письменника ви знаєте?

ІІІ. Розминка.

Інтерактивна вправа «Мозковий штурм».

Червона шапочка була дуже допитливою дівчинкою і про все, що її цікавило завжди у всіх питала.

• Скільки сонечок на небі?
• Скільки вух у зайця?
• Скільки сторін має трикутник?
• Скільки днів у тижні?
• Відрізок – це геометрична  фігура яка має ….

IV. Каліграфічна хвилинка.

Учитель. -  Що приготувала Червона Шапочка для бабусі?

( Фрукти, торт, молоко,?)

• Порахуйте скільки пиріжків взяли з собою?

Гра, Так чи не так?

Діти. – Не так. Вона взяла 7 пиріжків.

Учитель. – Сьогодні на каліграфічній хвилинці ми пригадаємо, як правильно писати цифру 7.

• «Мозковий штурм»

Учитель. Пригадайте, що ви знаєте про число 7? (сусіди, попереднє число, наступне число, які числа більше, які менше, склад числа7).

(Учитель пояснює написання цифри, діти прописують в зошиті).

V. Усний рахунок.

Колективна робота

1) Ось Червона Шапочка взяла кошик з пиріжками і пішла до бабусі. Яким шляхом йшла дівчинка?

Логічна вправа: «Систематизація»

(Дерева, кущі, птахи, чисте повітря, дикі тварини, гриби, квіти – ліс).

• Щоб не було сумно іти стала рахувати.

а) рахуємо разом 1 – 10, 10 – 1.

2) рахуємо 1ряд – від 2 до 8

                    2 ряд від 7 до 3

 3 ряд від 4 до 9

3)Червона Шапочка дуже любила читати і знала багато казок. Назвіть казку, порахуйте покажіть відповідь.

 

 

    0   1   2   3   4   5   6    7   8   9   10

• Купить і Верть зерно з поля носили,

Бо дуже вони пиріжки любили,

Вертю вдалося лише два відшукати.

Порахуйте, любі малята, скільки зернят знайшли мишенята (7з.)

• На яворі високім Телесик сидить

Зграя гусей до нього летить

Троє попереду, та позаду шість.

Скільки в зграї їх, скоріш полічить? (9г.)

• Знають діти казочку про Червону Шапочку.

До бабусі вона йшла, вісім пиріжків несла.

Раптом вовк її зустрів, пиріжків аж 4 з’їв.

Хто з вас діти порахує

Скільки пиріжків бабуся покоштує? (8 – 4 = 4п.)

4) Диференційована робота.

Вибрати завдання.

 

 

 

Слабкий рівень                               Середній рівень                   Високий рівень

10, ..7, …3,                                       3 + 4 =                                      6 + … =10

                                                          8 – 3 =                                      7 - …= 5

                                                          7 + 2 =                                      5 + … = 8

VI. Актуалізація опорних знань.

Далі йде червона Шапочка лісом по прямій дорозі, вже втомилась і вас: «Коли ця пряма закінчиться?»

Діти відповідають: «У прямої немає ні початку, ні кінця).  

Втомилась дівчинка, поставила з одного боку дороги камінець і присіла.  

Яка геометрична фігура вийшла?

Чи правильно відповіла Червона Шапочка : «Промінь – це геометрична фігура, яка має і початок і кінець?»

Але їй швидше хотілося потрапити до бабусі і тому вона, пройшовши декілька кроків знову поставила на прямій камінець.

• Яку геометричну фігуру отримала Червона Шапочка?

Складіть твердження: «Відрізок – це геометрична фігура, яка має …»

VII. Повідомлення темы мети уроку.

• Сьогодні ми уточнимо поняття «довжина», дізнаємося як можна вимірювати довжину відрізків і яким приладом це роблять?
• Йде дівчинка далі і зустрічає:

Загадка. Хвіст пухнастий, хутро золотисте,

               В лісі  живе, а в селі курей краде.

• Що знаєте про поведінку цієї тварини?
• Личка хитра, хоче обманути Червону Шапочку і показує їй найдовшу доріжку до хатинки бабусі.

1. Поняття «довжина».

• Порівняйте предмети. Що довше?

Але окомір може бути не точним. Порівняйте на ваших партах, що довше ручка чи олівець? Як ви дізналися? (способом прикладання).

• А якщо потрібно порівняти за довжиною два різних дивана. Чи можна використати спосіб «прикладання»? Що ж робити?

2. Мірки

а) Щоб виміряти довжину будь якого предмета використовують різні мірки. Декілька століть назад довжину та відстань вимірювали такими мірками: п’ядь, лікоть, сажень, верста.

Пригадайте, якими мірками вимірювали довжину удаву у мультфільмі «38 папуг»?

б) Давайте і ми виміряємо довжину вашої лінійки довжиною гумки. Чим буде при цьому довжина гумки? (Нашою міркою).

     3) Ознайомлення з см лінійкою.

Практична робота

 а) У Вас на партах є смужка і 2 мірки (1см, 3 см) поміряйте довжину вашої               лінійки цими мірками. Скільки разів помістилося маленької мірки? Велика мірка?

- Чому вимірюючи одну й  ту саму смужку ви отримали різні числові значення?

Висновок: треба використовувати однакові мірки. За одиницю вимірювання довжини прийняли сантиметр – це найбільш точна одиниця вимірювання довжини.

Ось ця маленька смужка є моделлю 1 см. Чи зручно нею буде вимірювати відрізки?

б) лінійка

Для зручності і швидкості вимірювання довжини відрізків люди придумали прилад.

Загадка. Точні поділки я маю,

                Всіх предметів визначаю

                Довжину і ширину,

 Висоту і товщину.

 Поруч себе олівець.

 І Між точками йому

 Чітко визначу межу. (лінійка)

Давні люди використовували для креслення дерев’яні дощечки. Дерев’яну лінійку з  поділками спочатку мали тільки вчені. Потім її стали виготовляти для студентів. У звичайні школи лінійка прийшла 100 років тому.

Логічна вправа. « Чи права Світланка?» Світлані мама купила лінійку і олівець.

«От,- каже Світлана - , гратимусь»

• Чи права Світлана?
• Складіть твердження: «Лінійка і олівець використовуються для …?»

Фізхвилинка.

в)шкала лінійки.

Учитель. – Роздивіться лінійку. Що бачите на ній? (Поділки позначені  цифрами).

• Початок відліку позначено цифрою 0. Які цифри ще написані? Рисочки і цифри, що нанесені на лінійку утворюють шкалу. Розгляньте частину шкали від 0 до 1. Ця частина утворює мірку, яка називається 1 см.

Уся шкала лінійки розбита на сантиметри довшими поділками, біля яких стоять цифри. Відстань між сусідніми цифрами дорівнює 1 см.

• Як же виміряти довжину предмета? Початок вимірюваного предмета (відрізка), ставимо навпроти цифри 0 , на якій цифрі закінчується вимірюваний предмет, така і його довжина.

Х. Формування вимірюваних навичок і умінь.

1) робота в підручнику (с. 45, Завдання 1)

Робота в парах (завдання 2).

2) робота в зошиті.

Давайте накреслимо відрізок, довжина якого 1 см. (Це 2 клітинки).

• Креслимо відрізок, довжини якого = 6 см.

ХІ. Геометричний матеріал.

Лисичка, ведмедик потоваришували з Червоною Шапочкою, знайшли разом до бабусиної хатинки найкоротшу дорогу і обігнали вовка.

 

 

 

 

 

 

 

 

 

 

 

 

• З чого складається будиночок?
• На які множини можна розділити геометричні фігури?
• За я кою ознакою ви зробили?
• Скільки трикутників пішло на його будівництво?
• Скільки чотирикутників?
• Скільки всього використано геометричних фігур?

А бабуся залишилася цілою і неушкодженою. Вовк так і не з’явився? Чому7

ХІІ. Підсумок уроку.

• Що нового дізналися на уроці?
• Продовжте  твердження: «Сантиметр – це одиниця вимірювання …»
• Яким приладом вимірюють довжину?
• Де будете використовувати набуті знання?
• Чи хочете нових зустрічей з нашими героями?

 

 

 

 

Урок з української мови в 3 класі на тему: «Слова близькі за значенням (синоніми).  Практичне ознайомлення з фразеологізмами, пояснення їх шляхом добору синонімів».

 

Вчитель початкових класів:

Андрущенко Валентина Миколаївна

 

Урок української мови (3 клас).

Тема: Слова близькі за значенням (синоніми).  Практичне ознайомлення з

     фразеологізмами, пояснення їх шляхом добору синонімів.

Мета:

   - дидактична: розширювати знання учнів про слова, близькі за значенням

    (синоніми), формувати вміння добирати синоніми, вживати їх в мовленні,

    збагачувати словниковий запас фразеологізмами.

   - розвиваюча: звивати мовне чуття, зв'язне мовлення, образне мислення, вміти порівнювати, пам'ять учнів.

   - виховна: виховувати любов до української мови, інтерес до вивчення логіки.

Тип уроку: Урок засвоєння нових знань, інтегрований урок (українська мова-логіка).

Форми роботи: Пари, групи, колективи.

Обладнання: Підручник “Рідна мова” (3клас) автор М.С. Вашуленко, демонстраційний матеріал, роздатковий матеріал, алфавіт, план уроку.

Епіграф уроку:

Плекайте діти,

рідну свою мову,

вчиться складно говорити

своїм рідним словом.

 

Хід уроку

I.Організаційна частина.

Сьогодні у нас незвичайний урок, сьогодні ми зробимо ще один крок. В країну казкову, в країну чудову, що так збагачує нашу мову.

В яку країну  ми зробимо сьогодні кроки? Складіть твердження: “ Сьогодня ми подорожуємо у країну ...”

II.Актуалізація знань учнів.

1) Перевірка домашнього завдання (підручник вправа 136)

    Учитель — Прочитайте пари слів, поясніть значення кожного слова.

                        Які слова називаються омонімами?

2) Гірлянда асоціації? (логічна вправа)

    Учитель — Впишіть відповідні слова-амоніми

Дверка        приклад для написання

Ніжність      звір

Біля, поблизу     геометрична фігура

 

III.План уроку

- каліграфічна хвилинка

- словникова робота

- ознайомлення з новим матеріалом

- фразеологізми

- поглиблення знань

- домашнє завдання

- підсумок уроку

IV. Каліграфічна хвилинка

V. Мотивація навчальної діяльності

Учитель - Для чого виконуємо каліграфічну хвилинку?

Діти       - Повторюємо графічне зображення букв, їх з’єднань з іншими буквами, вчимося каліграфії

                 зи  им  ма

Учитель - На які з’єднання букв треба звернути увагу?

Діти        - Верхнє, середнє і нижнє.

Учитель - Яке слово заховалося в цих з’єднаннях?

Діти        - Слово - зима.

Учитель – Пропишіть каліграфічно правильно це слово.

VI. Словникова робота.

Інтерактивна технологія. Робота в парах.

Учитель - До якої частини мови належить це слово? Чому?

Доберіть спільнокореневі слова до цього слова які належать до різних частин мови.

 

(зима,   зимуючий,  зимувати,   зимно).  Завданням з логічним навчанням.

Учитель - До якого поняття належить слово зима?

Діти        - До абстрактного.

Учитель - Дайте визначення цьому поняттю.

Діти        - Зима – пора року, коли промені сонця косо падають на землю і в зв’язку  з цим відбуваються деякі зміни, як в живій так і в неживій природі.

VII. Вивчення нового матеріалу.

1). Робота в підручнику.

Учитель - Прочитайте текст “Іде зима” (Вправа 139)

                - Які недоліки ви помітили в тексті?

                - Як можна допомогти вдосконалити твір?

Діти        - У тексті повторюються одні й ті самі слова. Треба замінити ці слова словами, близькими за значенням.

2). Оголошення теми і мети уроку.

Учитель - Сьогодні будемо вчитися добирати слова близькі за значенням, а називаються ці слова – синонімами.

3). Редагування тексту вправи (колективно). 

4). Творче завдання. Робота «ланцюжком».

Учитель - У вас на картках записані слова. Треба по черзі дібрати до них слова – синоніми. Деякі літери у відповіді вже записані:

       дорога       – п.ть, ш..х

       алфавіт      – аз...а, аб...а

       майдан       – пл...а

       бажати       – х....и

                  куняти       – др....и

       думати       – мі......и

       збагнути    – зр......и

                  борошно    – ....

Інтерактивна технологія. Робота в групах, кожна група отримує синонімічний ряд і складає з ним речення.

Фізхвилинка.

Ми писали,

ми трудились,

наші пальчики втомились.

Ручками махаємо,

метелика хапаємо.

Ворушимо пальчиками,

пальчиками-хапальчиками.

Ми їх добре розімнемо

 і писати знов почнемо.

5). Інтерактивний метод. Асоціативний кущ. Все що належить до народної творчості?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

VIII. Ознайомлення з фразеологізмами.

1). Ознайомлення с поняттям «фразеологізми».

Учитель - Фразеологізм – єдність кількох слів в словосполученні, або в реченні, які відтворюються в мові автоматично, за традицією. До них відносяться приказки, крилаті вислови. У фразеологізмах відображаються спостереження людини за своїм оточенням.

2). Спостереження за роллю фразеологізмів у мові.

      Робота в підручнику (вправа 144)

Учитель – Давайте колективно прочитаємо фразеологізми і з довідки виберемо синонім, який розтлумачує значення цього фразеологізму.

IX. Закріплення вивченого матеріалу.

1). Колективна робота.

      – З’єднати стрілочками фразеологізм і словосполучення, яке має з ним однакове значення.

Не второпаю      не під силу

Не до снаги      з дорогою душею

Відібрало мову     не збагну

За милу душу      заціпило

2). Гра «Так - ні».

      Вибрати хибне судження, перетворити його на істинне.

• синоніми – це слова однієї частини мови, різні за звучанням і написанням, що мають дуже близьке значення;
• фразеологізми – стійкі вислови, які використовуються в нашій мові;
• омоніми – це слова, які однаково звучать та пишуться, але мають різне значення.

X. Домашнє завдання.

       – Виконати вправу 145.

       Творче завдання: дібрати два фразеологізми, розкрити їх зміст, ввести в речення.

XI. Підсумок уроку.

1). «Рефлексія»

      – Які враження від уроку?

      – Що здалося найцікавішим?

      – Що нового дізналися?

• Про що б хотіли дізнатися в темі «Слово»?

XII. Оцінювання роботи учнів.

 

 

 

 

 

 

 

 

 

 

 

 

Урок з українського читання в 4 класі на тему: «Байки Леоніда Глібова».

Вчитель початкових класів:

Андрущенко Валентина Миколаївна

 

Урок позакласного читання (4 клас).

Тема: Байки Леоніда Глібова.

Мета:

          - дидактична: закріпити знання учнів про жанрові особливості байки, учити

            знаходити аналогії між зображеннями у байках і вчинками людей, формувати

            вміння працювати над байкою, визначати мораль байки.

          - розвиваюча: розвинути образне мислення, навчити виразного читання, культуру

            мислення через побудову міркувань, тверджень, умовиводів.

          - виховна: виховувати почуття милосердя, порядності, товариства; виробляти негативне ставлення до егоїзму, ліні, брехні.

Тип уроку: урок  закріплення знань (українського читання, логіки)

Обладнання: Виставка книжок, ілюстрація до байок, портрет Л. Глібова.

Форма уроку: урок-подорож.

Епіграф: Байка вчить, як на світі жити.

Хід уроку.

I. Організація класу

Учитель – Розпочинаємо урок читання.

                  Давно ці слова звучать у класі, адже читати ми навчилися давно.

                  Інтерактивна вправа «мозковий штурм».

                  Чого навчає урок читання в 4 класі? Твори яких жанрів ми читали?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Учитель – Які особливі задачі ставите перед собою, приходячи на урок читання?

Побудуйте твердження : «Я перед собою ставлю такі задачі...»

II. Задачі уроку. Мотивація навчальної діяльності.

Учитель. – Я як учитель ставлю перед собою задачу оволодіти українською літературною мовою, підготуватися до вивчення предмета «Українська література» в 5 класі яка:

    – вчить літературній мові;

    – збагачує особистість людини;

    – формує особистість людини.

Все це допоможе вам бути успішними у дорослому житті.

III. Повідомлення теми і мети уроку.

Учитель – На сьогоднішньому уроці «Чи знаєш ти байки Л. Глібова»?

ми закріпимо ваше уявлення про байку, удосконалимо вміння виразно читати  байки, будемо продовжувати оцінювати вчинки героїв, знаходити мораль у байці, робити узагальнення.

План нашого уроку

1. Мовна розминка.

2. Цікаві повідомлення.

3. Знайомство з байками Л. Глібова.

4. Сходинки творчості.

5. Підсумок уроку.

IV. Робота над темою уроку.

1). Мовна розминка.

      Гра «Хто це?».

      - сильний, злий, зубастий, сірий. (Вовк)

Учитель – Яке це поняття? (конкретне)

      - пухнастий, лагідний, спритний, полюбляє молоко і рибу. (кіт)

Учитель – До якого поняття належить це слово? (конкретне)

                  В яку множину можна об’єднати ці два поняття? (тварини)

                  Що можете розповісти про поведінку цих тварин?

2). Цікаві повідомлення.

Учитель – В Україні байки писали Петро Гулак, Левко Боровиковський, але

 найвидатнішими байкарями стали Євген Гребінка та Леонід Глібов. Нагадаю

 деякі дані цього славетного байкаря.

Л.Глібов народився 5 березня 1827 року на Полтавщині. У дитинстві його називали Льончиком. Він дуже любив квіти. У 13 років розпочав навчатися у Полтавській гімназії де і став писати вірші. Більшу частину життя прожив у Чернігові, працював у школі. В останні роки життя дуже хворів, майже втратив зір. Проте саме в той час Л. Глібов написав багато віршованих загадок, пісеньок, акровіршів для дітей. Однак найбільшою доробкою Л. Глібова стали його байки, їх написано 107.

Дерево знань:

 

Стрибунець       Лисиця і виноградар

 

Байки Л. Глібова                              Синиця

 

Чиж та голуб                                                                        Вовк і кіт

 

                                     Лебідь, щука і рак

 

Помер Л.Глібов у 1893 році і похований у Чернігові на подвір’ї Троїцького монастиря.

Учитель – Давайте пригадаємо що таке байка? (Байка – невеликий,

найчастіше віршований, твір повчального змісту. У байках в образах тварин, рослин, різних предметів зображено людей).

3). Робота над байкою «Вовк і кіт».

Учитель – Прочитали байку Л. Глібова «Вовк і кіт»? Які дійові особи є у байці? Вибіркове читання.

                – Прочитайте слова Вовка. Дайте характеристику цій тварині (хитрий, жадібний,  безтурботний, безвідповідальний).

                – Прочитайте слова кота. Дайте характеристику цій тварині (добрий, розсудливий, турботливий).

                – Прочитайте які імена зустрічаються у байці? (Степан, Дем’ян, Трохим, Клим)

– Яке ставлення автора до поведінка Вовка? Прочитай мораль байки. (Що братику посієш, те й пожнеш).

– Чи засуджуєте ви поведінку Вовка? Може вам шкода його? Чому? Що ви Можете порадити тим, хто поводиться так як Вовк?

– Якщо б можна було дописати байку, як би ви це зробили?

– Виразне читання байки в особах.

Фізхвилинка.

4). Опрацювання байки «Синиця».

Учитель – Прочитайте текст байки «Синиця», які дійові особи байки? Що можете розповісти про поведінку цієї пташки?

             – Повторне читання байки (колективно).

– Виразне читання.

Учитель – Про яку свою справу розповіла пташка? Прочитайте, що спричинила ця новина?  

                – Гра «Доповни речення».

                   «А пересудливі жінки...»

                   «От чують вони...»

                   «Так що ж синиця?...»

Учитель – Прочитайте мораль байки. (А ти ніколи не хвались, коли гаразд не зробиш діла).

Учитель – Як ви розумієте ці слова? Від чого застерігає автор? (Не кажи гол, поки не перестрибнеш) – народна приказка.

IV. Робота з байкою, складеною учителем та учнями.

       Знавці прекрасного

       Зозуля з Півником

       Прийшли до Соло’я.

       Його послухали, в долоні поплескали,

       А потім вийшли і сказали:

       Пищить, неначе немовля!

       Отак знавці і порішили:

       Співають пісні солов’ї.

       І марно витрачають сили!

       Кричали б краще на зорі

       Нажаль і серед нас ці

       Півники бувають

       Чого не вміють – зневажають.

Учитель – Хто є дієвими особами байки? Як поводилася Зозуля із Півником, коли гостювали у Солов’я? (Схвалювали його спів, плескали у долоні.) Як змінилася поведінка коли вони вийшли від солов’я? (Почали виказувати своє незадоволення.)

            – То чи можна вважати Зозулю та Півня знавцями прекрасного?

– Що можна сказати про Солов’я? (Добре співає, привітно зустрічає гостей.)

– Які якості висміює байка?

Характеристики дійових осіб

Негативні якості	Позитивні якості
Брехня, заздрість, невченість	Гостинність, талант, скромність

 

(Необхідно пізнавати прекрасне, не оцінювати, в чому сам не розумієшся.)

V. Підсумок уроку.

     Пропоную дітям розглянути виставку творів Л. Глібова.

Учитель – Байки – чудовий скарб мудрості. Рядки з багатьох байок стали крилатими висловами. Ними можна охарактеризувати людей та їх вчинки.

Л. Глібов писав:

     Здається, байка просто бреше,

     А справді явну правду чеше,

     Нікого в світі не мине,

     Читайте, радуйте мене.

 

 

 

Ігри та вправи, що розвивають логічне мислення.

 

 

 

 

Додаток 1

“ЛОМИГОЛОВКА З ПАЛИЧКАМИ”

Це гра для розвитку у дитини здатності подумки перегруповувати елементи об'єкта і планувати свої дії подумки.

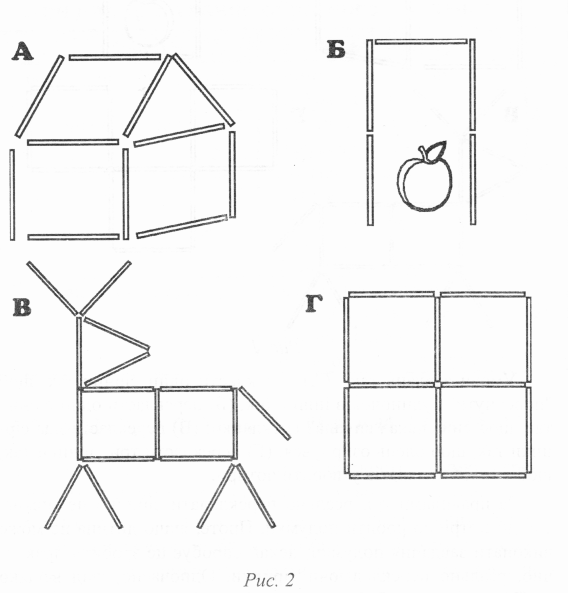
Візьміть кілька паличок або сірників і складіть з них схематичне зображення якого-небудь предмета. Після цього запропонуйте малюкові подумки перекласти один або кілька сірників так, щоб перетворити це зображення на інше або якось його змінити. На рисунку 1 показані декілька таких завдань.

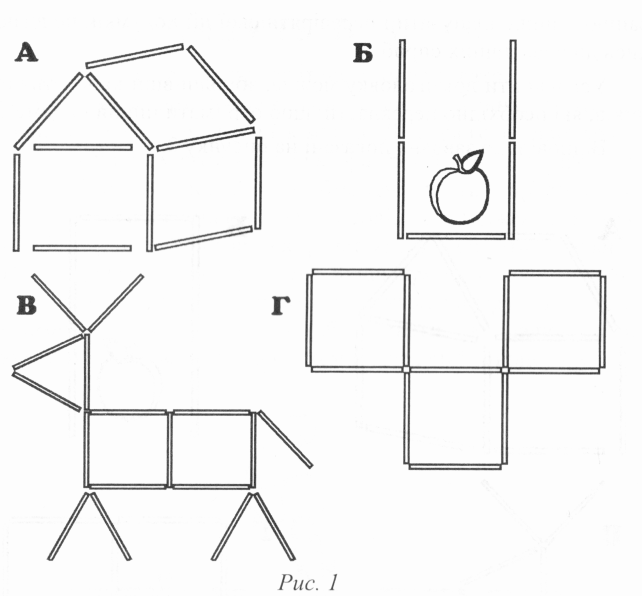Умови завдань такі: (А) перекласти один сірник так, щоб "повернути" будиночок в інший бік; (Б) перекласти один сірник так, щоб вишенька “випала” із склянки; (В) перекласти два сірники так, щоб олень озирнувся; (Г) перекласти три сірники так, щоб з трьох квадратів утворити чотири.

За правилами гри реально перекладати сірники не можна. Усі дії потрібно робити подумки. Проте, якщо дитина не може виконати завдання подумки, нехай спробує це зробити практично, реально перекладаючи сірники. Одночасно, слід всіляко подбати про те, щоб малюк навчився здійснювати перетворення предмета подумки. Тільки така форма гри сприятиме формуванню вміння планувати і перевіряти свої дії подумки, не вдаючись до практичних спроб.

Ускладнити ломиголовку можна, збільшивши кількість сірників, які необхідно перекласти, щоб отримати інший предмет.

Відповіді до завдань показані на рисунку 2.

 

 

 

 

 

 

 

 

 

 

"НАКРЕСЛИ ПЛАН-КАРТУ"

У цю гру краще грати лише після того, як дитина зможе успішно виконувати завдання гри "Де ховається папуга?". Приготуйте аркуш паперу в клітинку і олівець (фломастер).

Мета гри — навчити дитину створювати план-карту знайомого їй простору, наприклад, своєї квартири або дитячого майданчика, де вона грається. Поясніть малюкові, що люди створюють такі план-карти для того, щоб легше було орієнтуватися на місцевості. Покажіть йому, наприклад, карту міста, в якому ви живете, і трошки розкажіть про неї.

Після того запропонуйте малюкові скласти план-карту квартири, в якій він живе. Перед тим, як він почне її рисувати, попросіть його описати те, що знаходиться у цій квартирі, особливості її планування. Нехай вибере ті предмети, які, на його думку, повинні бути відображені на план-карті, а також умовні позначки, які будуть використовуватися для відображення цих предметів (при виборі позначень можете надати дитині допомогу). Коли все це буде зроблено, можна починати креслити.

Після того як буде створена план-карта квартири, перейдіть до складання план-карти того місця, де знаходиться ваш будинок чи дитячий майданчик, на якому малюк звичайно грається. У цьому випадку важливо відразу обмежити ділянку місцевості, яка повинна увійти в карту і за межі якої "виходити" не можна. На карті цю ділянку потрібно позначити прямокутною рамкою і вказати орієнтири, що знаходяться за її периметром (наприклад, це може бути якийсь паркан, що оточує дитячий майданчик, чи доріжки в скверику, які відділяють його від зелених насаджень).

Під час складання план-карти діти найчастіше роблять такі помилки: 1) "випускають" з уваги важливі деталі планування; 2) порушують розміщення предметів у просторі, їх положення відносно один одного; 3) не позначають деякі предмети; 4) спотворюють розміри предметів, які вони відображають (наприклад, менші за розміром предмети позначають більшими фігурками, а більші предмети — меншими).

Такі помилки цілком природні для дітей цього віку. Головне, щоб ви звертали на них увагу і пояснювали малюкові, в чому полягає помилка. Старайтеся досягати того, щоб він самостійно або з вашою допомогою виправляв усі помилки. Саме від цього залежить розвиваючий ефект гри.

“ПРОГНОЗ ПОГОДИ”

 Розкажіть малюкові, що люди придумали зображати погоду з допомогою простих малюнків. Вони необхідні для того, щоб без зайвих слів повідомляти усім, для кого це важливо, які сюрпризи може зробити природа найближчим часом. Такі малюнки можна побачити на екрані телевізора, коли передають прогноз погоди. Аналогічні малюнки метеорологи використовують для складання карт погоди. Такими картами користуються, для прикладу, моряки і льотчики.

Після такої короткої розповіді попросіть дитину придумати, яким малюнком вона б позначила ясний сонячний день, дощовий день, снігопад, похмурий день (коли небо захмарене), дощ з грозою, вітряний день, легке хвилювання на морі, шторм, сонячний день з невеликою хмарністю, дощ зі снігом і т.д. Дайте дитині можливість на окремих аркушах паперу намалювати різні варіанти схематичних зображень погоди. Якщо виникнуть ускладнення, обговоріть з нею, що можна намалювати, щоб усі могли зрозуміти, що сьогодні буде, наприклад, дощ. Малюнки повинні бузи дуже прості і такі, щоб їх легко можна було розпізнавати. Вони можуть виглядати приблизно так, як на рисунку 4.

На рисунку показані такі схематичні зображення погоди: сонячно (1), дощ (2), сніг (3), похмуро (4), дощ з грозою (5), вітер (6), шторм (7), дощ зі снігом (8), град (9), ураган (10).

Після того як ви разом з дитиною зобразите різноманітні прояви погоди, можна починати гру. Вона може проходити у двох варіантах. Ви, як ведучий, повідомляєте малюкові з допомогою "рації", яка буде погода (вітряна, дощова, похмура), а він знаходить відповідні картки і вивішує їх на стенді "Інформація для льотчиків і моряків". Замість такого стенду можна використати аркуш паперу з відповідною назвою. Як відомо, погода змінюється часто. Тому, після того як дитина виконає завдання, ви знову повідомляєте про зміну погоди, наприклад, про те, що очікується сонячна погода, але можливі вітер і шторм.

Другий варіант цієї гри дозволяє малюкові вчитися самостійно розповідати про погоду з допомогою схематичних зображень. Для цього запропонуйте дитині стати диктором телебачення і повідомити, яка погода буде сьогодні і завтра. А ви будете метеорологом, який показує дикторові картки з прогнозом погоди.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

“ЗБЕРИ ЗА СХЕМОЮ”

 Гра розвиває вміння орієнтуватися в схематичному зображенні предмета і здатність конструювати.

Для гри можна використати будь-який будівельний конструктор, до складу якого входять такі деталі, як кубики, бруски, вежі, арки та ін. Крім того, слід приготувати схематичні зображення зібраних з цих деталей конструкцій (наприклад, катка, підводного човна, вежі та ін. — див. рис. 7). Кожна деталь такої конструкції повинна бути чітко прорисована.

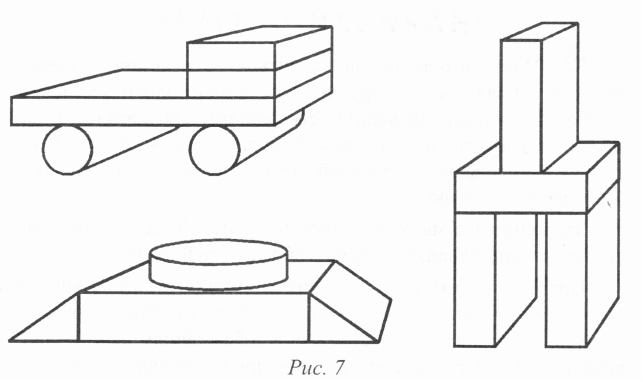
Ви показуєте дитині схематичне зображення одної із конструкцій, а вона повинна зібрати її з деталей, які є в її розпорядженні. При цьому зверніть увагу малюка на те, щоб зібрана ним конструкція докладно відповідала схемі.

Перш ніж розпочати конструювання, нехай малюк назве зображений предмет, розповість про його призначення, виділить найважливіші частини і опише їх форму. Після того як конструкція зібрана, проаналізуйте разом з дитиною, чи все вона зробила правильно, розгляньте помилки, підкажіть, як їх можна виправити.

Щоб ускладнити гру, можна збільшити кількість деталей, які використовують для конструкції. Другий спосіб ускладнення — показувати схематичне зображення протягом короткого часу, після чого просити малюка зібрати конструкцію з пам'яті. Тоді гра сприятиме розвиткові не лише образного мислення, але й образної пам'яті.

“ГРА В ПЕРЕСТАВЛЯННЯ”

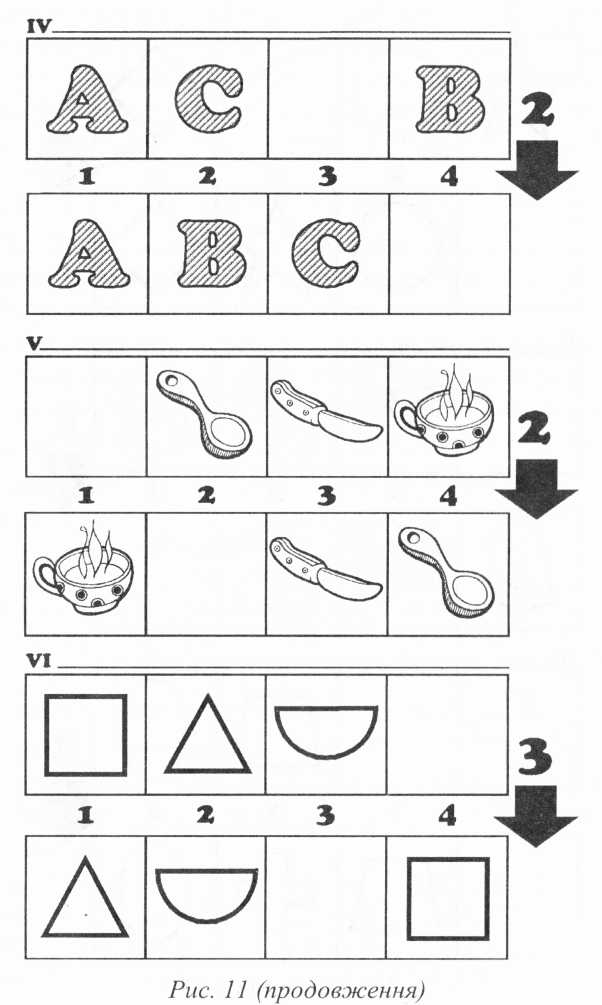
Ця гра сприяє розвиткові здатності планувати свої дії подумки. Для неї необхідно приготувати завдання, аналогічні до тих, що зображені на рисунку 11.

Починати краще з найпростіших завдань, які складаються з двох карток по 4 поля. На кожному з 3 полів знаходяться геометричні фігури. Одне поле пусте. Фігури на обох картках однакові, але місце їх розташування різне (див. рис. 11)

Перед початком гри запропонуйте малюкові уважно роздивитися фігури на обох картках і сказати, чим верхня картка відрізняється від нижньої. І лише після цього повідомте завдання гри. А воно таке. Необхідно з допомогою певної кількості переставлянь (ходів) розмістити фігури верхньої картки на ті ж місця, які вони займають на нижній. При цьому одним ходом можна переставляти лише яку-небудь одну фігуру і тільки на вільне поле. Кількість ходів вкажіть справа від пари карток.

Наприклад, щоб виконати завдання у першій грі (рис. 11,1), потрібно переставити на верхній картці зірочку з поля 1 на поле З (коротко цю відповідь можна записати так: 1-3). Відповіді до решти завдань такі:

 

II: 1)4-1; VI: 1) 1-4, 2) 2-1, 3) 3-2;

III: 1)3-2,2) 1-3; VII: 1) 4-2, 2) 1-4, 3) 3-1;

IV: 1)2-3, 2)4-2; VIII: 1) 2-4, 2) 1-2, 3) 3-1;

V: 1)4-1,2)2-4; IX: 1) 2-3, 2) 1-2, 3) 4-1, 4) 2-4.

 

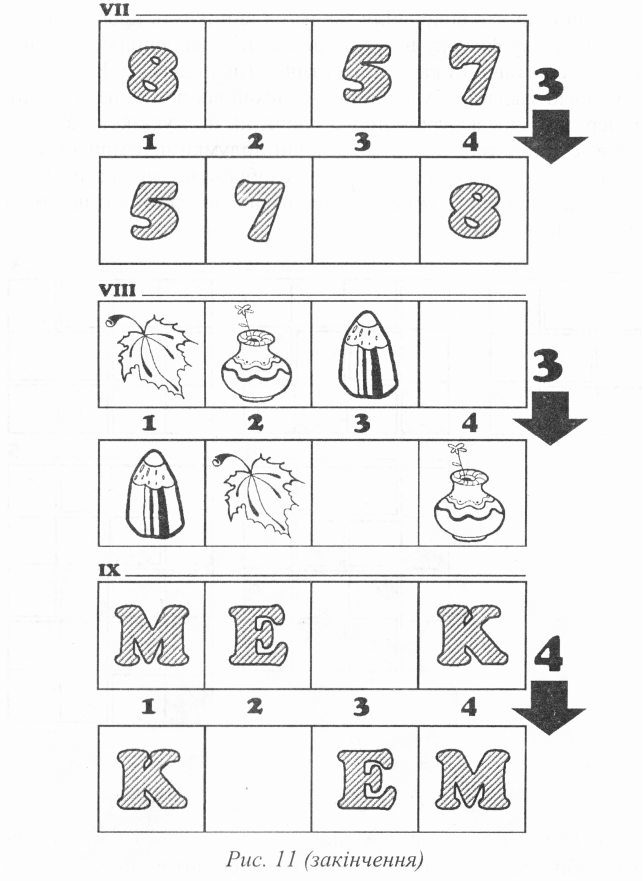Якщо під час виконання завдання виникнуть проблеми, зобразіть кожну фігурку на окремій картці і запропонуйте малюкові попереставляти картки практично (не подумки). Коли у такий спосіб завдання буде виконане, нехай він повторить свої дії, не пересуваючи фігури і не вказуючи на них указкою, а лише називаючи фігури і поля, на які вони подумки переміщені. Після цього знову поверніться до гри із зображеннями фігур. Лише переставляння їх подумки сприяє розвиткові здатності подумки планувати свої дії.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Додаток 2

 

 

 

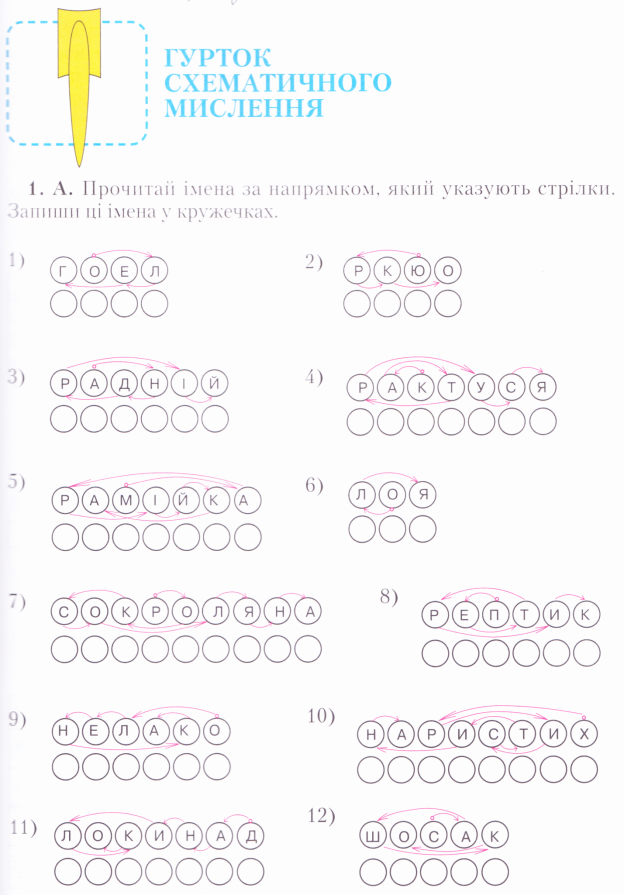
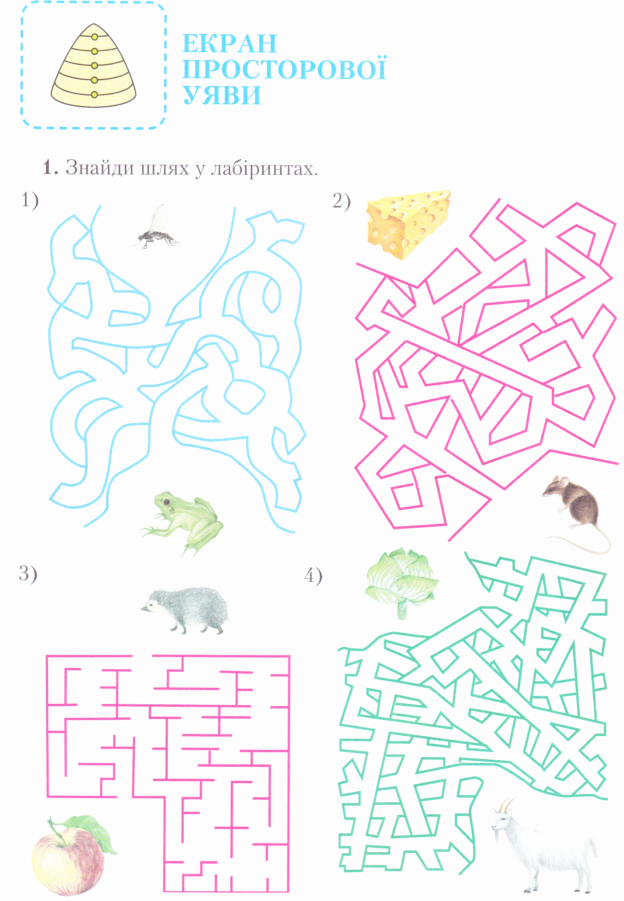
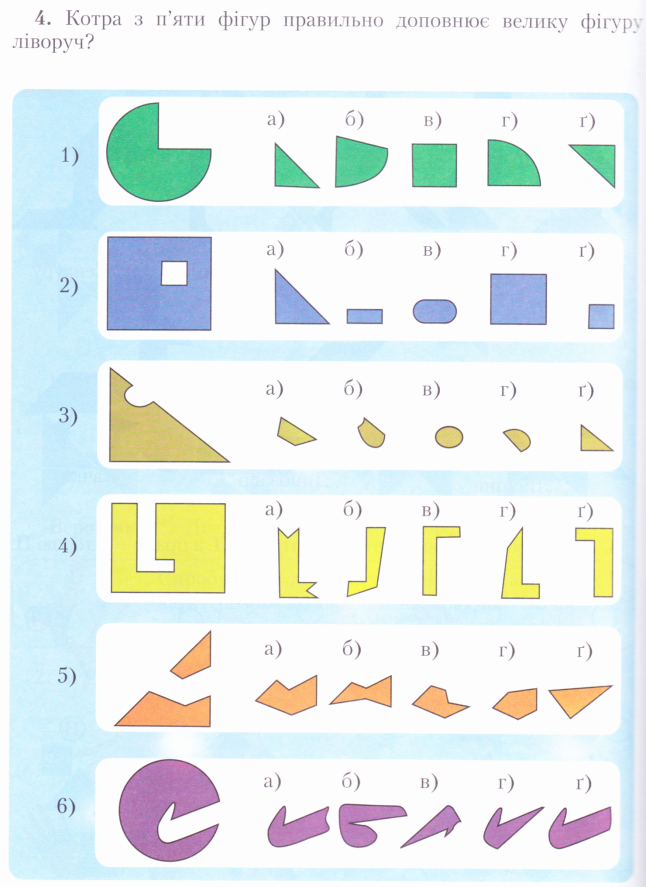
Додаток 3

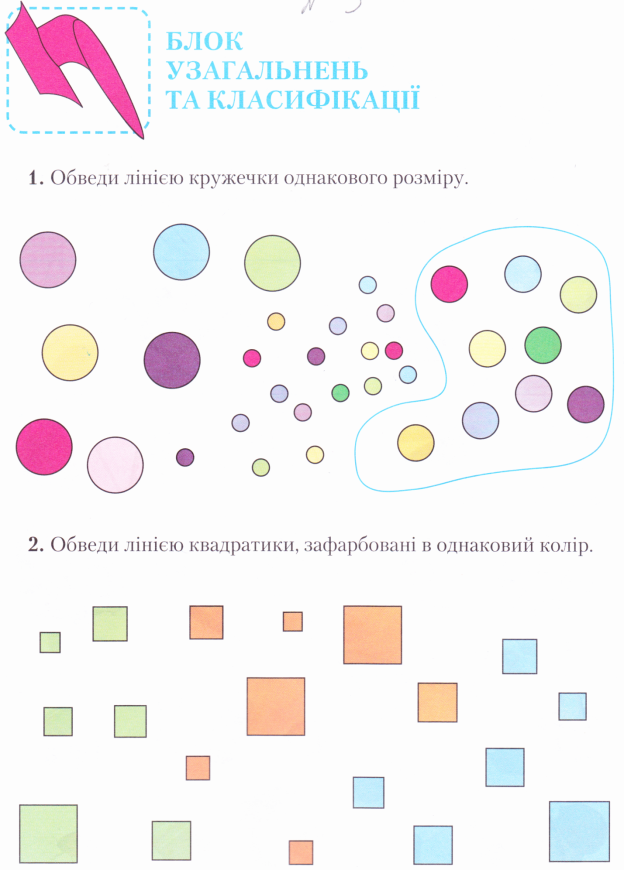
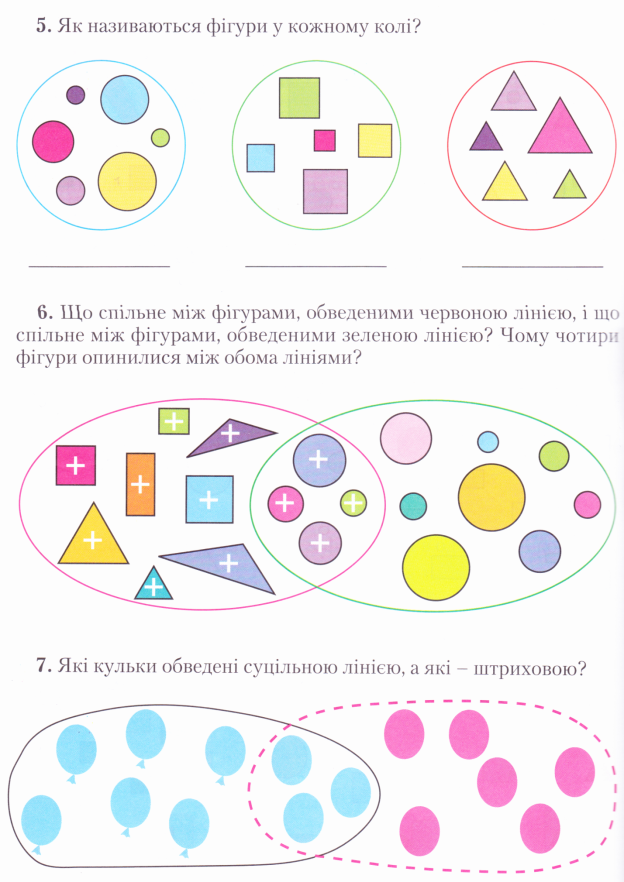
Додаток 4

Задачі для учнів 1 класу

1.  Біле сонячне світло складається із семи кольо­рів. Назвати ці кольори.

2.  Хто наймолодший?

За Юрка Андрійко старший,

Та молодший від Сашка.

Старший за Сашко Тарас.

Хто наймолодший серед нас?

3.  Двоє дівчаток повертаються зі школи додому, а назустріч їм ідуть троє хлопчиків. Скільки всього дітей повертаються додому?

4.  П’ятеро братів мають кожен по одній сестрі. Скільки всього дітей у цій сім’ї?

5.  Двоє дівчаток вирізали 7 прапорців. Скільки прапорців могла вирізати кожна дівчинка?

6.  Які три однакові числа потрібно додати до 5, щоб отримати. 8?

7.  У скільки способів може вишикуватися в стрій команда з 3 осіб?

8.  Що буває наприкінці літа і на початку осені?

9.  Які із цих тверджень є правильними? Чому? Перед травнем був квітень, а після квітня буде

червень.

Якщо завтра вівторок, то сьогодні середа.

Ю.Що більше — дві трійки чи три двійки?

16.  Не виконуючи дію, скажіть, на скільки сума 10+1 більша за різницю 10-1?
17. Рухаючись від літери до літери, можна прочи­тати слово «трикутник». На малюнку зображе­но один із маршрутів. Чи зможеш ти відшукати інші маршрути?

Трикутник

рикутник

икутник

кутник

утник

тник

ник

икк

18. Скільки днів мине від неділі до неділі? Від се­реди до середи?
19. На столі лежать 3 олівці. Як переставити серед­ній олівець, не чіпаючи його?
20. «Скільки у тебе солдатиків?» — запитали Пет- рика. «Більше, ніж чотири, але менше ніж шість»,— відповів він. Скільки солдатиків має Петрик?
21. У Максимка є дві футболки — біла і блакитна. І дві пари шортів — зелені і чорні. У скільки способів він може одягнути спортивну форму? Зроби малюнки.
22. Бабуся зварила варення з малини. При цьо­му на кожній дві склянки ягід вона брала три склянки цукру. Скільки склянок ягід бабуся

взяла для варення, якщо всього вона витратила 12 склянок цукру?

 

Задачі для учнів 2 класу

1. На подвір’ї ходять вівці та кури, усього 14 ніг. Скільки було овець і скільки курей, якщо раЗОхМ було п’ять голів?
2.  Один годинник показував, що від початку фут­больного матчу минуло півгодини. Скільки ча­су від початку матчу покажуть два годинники?
3.  Семеро чекали восьмого 14 хвилин. Скільки хвилин витратив на чекання кожен?
4.  Запиши ряд чисел: 1, 2, 3, 4, 5, 6, 7, 8. Додай крайні числа, потім — другі, треті, четверті від кінців. Яку цікавинку ти помітив?
5.  Два плюс два, помножити на два — скільки буде?
6.  У двох носорогів два роги. Скільки рогів у два­дцяти носорогів?
7.  Трояндові кущі висаджують на однаковій від­стані один від одного. На першій ділянці виса­дили 10 кущів, на другій — 5, а на третій — 15. Який висновок можна із цього зробити?
8.  В автобусі було 17 осіб. На зупинці зайшло З і ввійшло 3. Збільшилася чи зменшилася кіль­кість пасажирів?
9.  Сьогодні п’ятниця. Який день тижня буде через 6 днів? 7 днів? 8 днів? 10 днів?
10. Скільки одиниць необхідно додати до оди­ниці, щоб вийшло число, записане двома одиницями?
11. Добери два числа, сума і різниця яких — одне і те саме число.
12. Відомо, що а - к - 0. Що можна сказати про числа а і /с?
13. Яких значень може набувати х у реченнях: «У місяці буває х днів», «Монети бувають вар­тістю х коп»?
14. Драбина має 17 щаблів. На який щабель по­трібно піднятися, щоб опинитися посередині драбини?
15. У скільки разів половина більша за свою по­ловину?
16. Водій автомашини має двох сестер, але вони не мають брата. Як це може бути?
17. У брата і сестри порівну яблук. Брат дав сестрі З яблука з тих, які мав. На скільки яблук стало більше у дівчинки?

 Задачі для учнів 3 класу

1.  Чотири колеса автомобіля пройшли кожне по 10 км. Яку відстань подолав увесь автомобіль?
2.  Учень записав числа від 1 до 100. Скільки разів він писав цифру 5? цифру 1? цифру 0? цифру 9?
3.  Записати число 10 трьома одиницями. Записати число 90 трьома дев’ятками.

4. У яких двоцифрових чисел сума цифр дорівнює найбільшому одноцифровому числу?
5.  Чи правильні такі вислови: в автобусі 42 місця, з них: 23 для сидіння і 19 для їзди стоячи; в автобусі       60 місць, з них: 32 для сидіння, а для їзди стоячи — на 4 місця більше; в ав­тобусі 55 місць, з них: 32 для сидіння і стільки ж для їзди стоячи?
6.  Назви два числа, де кількість цифр дорівнює кількості літер, з яких складаються назви цих чисел.
7.  За 3 хвилини колоду розпиляли на півметровки, причому кожне розпилювання займало одну хвилину. Знайди довжину колоди.
8.  Чим схожі і чим різняться числа: 4, 44, 94, 49?
9.  Не обчислюючи, скажи, як зміниться сума 34 + 17, якщо перший доданок зменшити на 2, а другий зменшити на 1?
10. Від початку доби минула 31 Година. Котра те­пер година?
11. До 3 допиши праворуч таку одну цифру, щоб вийшло число, яке ділилося б на 9; на 8.
12. У кожному виразі поставити дужки таким чи­ном, щоб його значення збільшилось:

3 + 4-8;

24 - 18 : 2 + 4;

24 : 6 - 2;

32 : 8 - 4;

42 - 24 : 3 + 3;

7-3 + 4.

15.Загадати число, додати до нього таке саме, су­му помножити на три, потім поділити на два, а те, що одержите, поділити на три. І завжди матимете задумане число. Перевірте.

16. Довести, що в місяці буває не більше ніж п’ять субот.

17. Написати на аркуші паперу свій розмір взуття. Це число помножити на 2, до добутку додати  5, суму помножити на 50, додати кількість своїх років, відняти число 250. Залежно від того, яке число отримано, можна дізнатися про розмір вашого взуття і ваш вік. Довести, що тут немає жодних «чарів».

Задачі для учнів 4 класу

1.  Які одноцифрові, двоцифрові та трицифрові числа можна читати перевернутими?
2.  Яке число, що закінчується цифрою 2, більше ніж 245 і менше ніж 263?
3.  У книзі остання сторінка позначена так: 128. Скільки сторінок у книжці? Скільки аркушів?
4.  Чи можна назвати всі можливі числа?
5.  Які з цих суджень є завжди правильними або завжди неправильними? Чому?

х У двох тижнях 14 днів.

^х Лютий іде за січнем. ^х У місяці ЗО днів. ^х У році 365 днів. ^х У місяці 28 днів. ^х Дві доби мають 50 годин. ^х Двоцифрове число менше одноцифрового. ^х Різниця більша за від’ємник.

6.  Кожна четверта книжка, видана в нашій країні, призначається для школи. Скільки книжок при­падає школі з кожної тисячі?
7.  У літрову банку вміщається 600 г брусниці чи 800 г вишні. Для яких ягід потрібна буде біль­ша банка, якщо купити їх по кілограму?
8.  Яка чверть року більша: перша чи друга? Друга чи третя?
9.  Знайти помилку: 96 : 32 = (90 + 6) : (90 + 2) = = (90 : 30) + (6 : 3) = 5.
10. Знайти у зручний спосіб суму чисел у рядках, користуючись сумою першого рядка:

5 + 3 + 7 = 15 105 + 103 + 107 =

15 + 13 + 17 =

205 + 203 + 207 =

25 + 23 + 27 =

11. Написати число 10 однією цифрою, яка повто­рювалась би 5 разів.
12. Чи можна сказати, не розв’язуючи рівняння 20 • х = 100, у скільки разів невідомий спів­множник менший від добутку?
13. У числі 598 закреслити крайню цифру ліворуч. Як змінилося число?
14. Що більше: сума всіх одноцифрових чисел чи їх добуток?

Білий ведмідь на 600 кг (у 5 разів) важчий за “"лева. Скільки важать ведмідь і лев окремо?

 

Додаток 5

 

 

 

Додаток 6

1. Через 9 років Андрій буде на рік старший, ніж Дарина тепер. Хто молодший? (Якщо Дарина тепер

     старша від Андрія, то Андрій завжди буде молодший від Дарини. Отже, Андрій молодший).

 2. Рік тому Дмитро був старший од Степана. Хто старший зараз? (Дмитро).

 3. Геннадій заліз на дерево вище від Данила. Хто заліз не так високо, як Геннадій? (Данило).

 4.Синій будинок вищий, ніж червоний, червоний — вищий, ніж зелений. Який із цих трьох будинків найвищий, а який — найнижчий? (Найвищий синій будинок, найнижчий — зелений).

 5.У Лариси вдома ляльок більше, ніж у Катрусі, у Вікторії ляльок більше, ніж у Лариси. У кого з дівчаток ляльок найбільше, у кого — найменше? (Найбільше ляльок у Вікторії, найменше — у Катрусі).

 6.Дуб грубіший од верби, а верба грубіша від берези. Яке дерево з цих трьох найгрубіше, яке — найтонше? (Найгрубіший з цих трьох дерев — дуб, найтонша — береза).

7. Володя хворів не так довго, як Леонід, Федір — не так довго, як Володя, Кирило хворів довше, ніж Леонід. Хто хворів найдовше? Розташуйте всіх дітей за часом тривалості хвороби — від найменшого терміну до найбільшого. (Кирило хворів найдовше. За часом тривалості хвороби діти будуть розташовані так: Федір, Володя, Леонід, Кирило).

 8.Вітя вчився гірше від Люди. Микола — гірше від Віті. Катя вчилася краще від Люди. Хто з дітей вчився найгірше? Хто вчився найкраще? (Микола вчився найгірше, Катя — найкраще).

 9.Денис сильніший від Любомира. Валентин сильніший від Сашка, а Сашко сильніший від Дениса. Хто з хлопчиків найсильніший? Хто з хлопчиків найслабший? (Валентин найсильніший серед хлопчиків, а Любомир — найслабший).