Урок на тему "Сума n перших членів геометричної прогресії."

Тема: Сума п перших членів геометричної про­гресії.

Мета: ознайомити учнів з формулою для обчис­лення суми п перших членів геометричної прогресії; формувати навички й уміння застосовувати форму­лу для розв'язування задач; розвивати логічне мис­лення, обчислювальні навички учнів; виховувати інтерес до предмета; показати зв'язок математики з життям.

Обладнання: таблиця значень степенів чисел 2 і З, таблиця квадратів натуральних чисел від 10 до 99.

1. Дати означення геометричної прогресії. (Слід звернути увагу учнів на те, що це послідовність відмінних від нуля чисел.)
2. Як можна задати геометричну прогресію?
3. Відомі перший член геометричної прогресії і знаменник. Як знайти десятий член?
4. Відомі будь-які два послідовні члени геомет­ричної прогресії. Як знайти знаменник?
5. Чи є послідовність геометричною прогресією:

а) 3; 3; 3; 3 ...;

б) 2; 0; 0; 0 ...;

в) 3; 6; 12; 24; 48...?

6. Відомо, що числа а₁, а₂, а₃... утворюють гео­метричну прогресію. Чи є геометричною прогресією послідовність 3а₁, 3а₂,3а₃ ...?

II. Повідомлення теми, мети, завдань уроку.

III. Вивчення нового матеріалу.

Учитель. Щоб зрозуміти ідею виведення форму­ли для обчислення суми п перших членів геомет­ричної прогресії, спочатку поговоримо про шахи. Не дивуйтесь цьому.

Шахи — одна з найдавніших ігор. Вона існує ба­гато віків, і не дивно, що з нею пов'язані різні пере­кази, правдивість яких через давність часу немож­ливо перевірити.

З однією з таких легенд ми сьогодні й ознайо­мимося. Щоб зрозуміти її, зовсім не треба вміти грати у шахи: досить знати, що гра відбувається на дошці, поділеній на 64 клітинки (чорні і білі).

Шахову гру було придумано в Індії, і коли індуський цар Шерам ознайомився з нею, він був у захопленні.

Довідавшись, що її винайшов один з його підда­них, цар наказав покликати його, щоб особисте нагородити за вдалу видумку.

Винахідник, його звали Сета, з'явився перед троном повелителя. Це був скромно одягнений учений, який заробляв на життя, навчаючи інших.

(Далі легенда переказується у вигляді сценки, підготовленої учнями класу. Діючі особи: цар Ше­рам, винахідник Сета, слуги, старшина придворних математиків.)

Цар Шерам. Я бажаю гідно нагородити тебе, Сето, за чудову гру, яку ти придумав.

(Мудрець вклонився.)

Цар. Я досить багатий, щоб виконати найсміливіше твоє бажання. Назви нагороду, яка тебе за­довольнить, і ти одержиш її.

(Сета мовчить.)

Цар. Не бійся, вислови своє бажання. Я не по­шкодую нічого, щоб виконати його.

Сета. Велика добрість твоя, повелителю. Але дай строк обміркувати відповідь. Завтра я повідом­лю тобі моє прохання.

Учитель. На другий день Сета знову з'явився в палаці.

Сета. Повелителю! Накажи видати мені за пер­шу клітинку шахівниці одну пшеничну зернину.

Цар (здивовано). Просте пшеничне зерно?

Сета. Так, повелителю. За другу клітинку на­кажи видати дві зернини, за третю — чотири, за четверту — вісім, за п'яту — шістнадцять...

Цар (роздратовано перебиває Сету). Досить. Ти одержиш свої зерна за всі 64 клітинки дошки, як бажаєш: за кожну вдвоє більше від попередньої. Але знай, що прохання твоє недостойне моєї щед­рості. Просячи таку мізерну нагороду, ти нехтуєш моєю милістю. Воістину, як учитель ти міг би показати кращий приклад поваги до милості й щедрості свого повелителя. Іди. Слуги мої вине­суть тобі твій мішок з пшеницею.

(Сета посміхнувся і покинув замок.)

Учитель. Після обіду цар згадав про винахід­ника шахів і надіслав слугу дізнатися, чи виніс не­розсудливий Сета свою мізерну нагороду.

Цар. Чи отримав Сета свій мішок з зерном?

Слуга. Повелителю! Наказ твій виконується. Придворні математики підраховують кількість на­лежних зерен.

(Слуга виходить.)

Учитель. Цар нахмурився, він не звик, щоб його повеління виконувалися так повільно. Увечері, іду­чи спати, цар ще раз звернувся до придворних.

Цар. Чи давно Сета зі своїм мішком пшениці покинув палац?

Слуга. Повелителю! Математики твої невтомно працюють і сподіваються ще до світанку закінчи­ти підрахунок.

Цар. Чому зволікають з цією справою? Завт­ра, до того, коли я прокинуся, все до останньої зернини повинно бути видано Сеті. Я двічі не наказую!

Учитель. Уранці цареві доповіли, що старшина придворних математиків просить вислухати важ­ливе донесення. Цар наказав йому зайти.

Цар. Перед тим, як ти казатимеш про інші спра­ви, я бажаю почути, чи видано, нарешті, Сеті ту мізерну нагороду, яку він собі сам призначив.

Старшина придворних математиків. Заради цьо­го я і насмілився з'явитися до тебе у таку ранню годину. Ми сумлінно полічили кількість зерен, яку бажає одержати Сета. Число це таке велике...

Цар (гордовито перебиває). Яке велике воно не було б, житниці мої не збідніють. Нагороду обіця­но і її треба видати...

Старшина придворних математиків. Ти не мо­жеш, повелителю, виконати таке бажання. У всіх коморах твоїх немає такої кількості зерен, яку за­жадав Сета. Немає його і в житницях цілого цар­ства. Не знайдеться стільки зерна і на всьому про­сторі Землі. І якщо бажаєш неодмінно видати обі­цяну нагороду, то накажи перетворити всі земні царства на поля, накажи осушити моря й океани, накажи розтопити лід і сніги, що вкривають да­лекі північні пустелі. Нехай увесь земний простір буде засіяно пшеницею. І все те, що виросте на цих полях, накажи віддати Сеті. Тоді він одержить свою нагороду.

Цар (після паузи роздумливо). Назви ж мені це дивовижне число...

Старшина придворних математиків. 18 квінтильйонів 446 квадрильйонів 844 трильйони 73 більйони 709 мільйонів 551 тисяча 615, о повели­телю!

Учитель. Така легенда. Чи справді було те, про що тут розповідалося, невідомо, але нагорода, про яку йшлося, мала бути саме такою.

Як швидше обчислити це число? Кількість зернин, про які йдеться, є сумою 64 членів геометричної прогресії, перший член якої

b₁= 1, а знаменник q =2. Позначимо цю суму че­рез S:

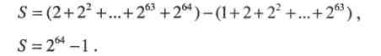
Маса такої кількості зерен більша за масу пше­ниці, зібраної людством до теперішнього часу.

Індуський цар не міг видати таку нагороду, але якби він знав математику, то легко міг би звільнитися від такого обтяжливого боргу. Для цього потрібно було лише запропонувати Сеті самому відлічити собі зернину за зерниною всю належну йому пшеницю.

Виведемо формулу суми п перших членів довільної геометричної прогресії. Скористаємося тим самим способом, за допомогою якого було обчислено суму зерен.

IV. Формування навичок і вмінь.

(Номери завдань вказано за підручником: Бевз Г.П. Алгебра: Проб, підруч. для 7—9 кл. серед, шк. — 2-ге вид. — К.: Освіта, 1997.)

№ 255 (а). Знайти суму 15 перших членів гео­метричної прогресії 1, 2, 4, 8, ...

№ 260. Було це майже 100 років тому. Селянин продавав 20 овець за 200 крб. Коли один з покупців став надто довго торгуватися, селянин запропонував: «Дай за першу вівцю одну копійку, за другу — 2 к., за третю — 4 к. і далі за кожну вівцю вдвічі більше копійок, ніж за попередню». Покупець погодився. Скільки він заплатив за тих 20 овець?

Розв'язання

Вартість овець, про які йдеться в задачі, є су­мою 20 членів геометричної прогресії, перший член

якої в₁ = 1, а знаменник q = 2. Тоді

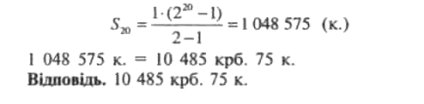
№ 261. Бактерія, потрапивши в організм, до кінця двадцятої хвилини ділиться на дві, кожна з них до кінця двадцятої хвилини знову ділиться на дві і т.д. Скільки бактерій стане в організмі через добу?

Розв'язання

Проілюструвати задачу можна таким малюнком:

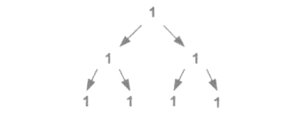
Очевидно, що за одну годину поділ бактерій прой­де тричі, за 24 год (тобто за добу) поділ бактерій відбудеться 3 • 24 = 72 (рази).

Отже,

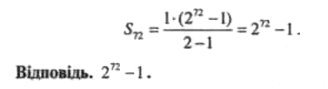
V. Підсумок уроку. 

VI. Домашнє завдання.

§ 61, № 255 (в), 257 (а, б), 263 (додатково).