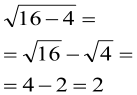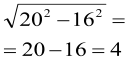Урок на тему: "Властивості арифметичного квадратного кореня"

КЗО “Спеціальна школа №12” ДОР

 

 

 

 

 

 

Відкритий урок

Тема: “Властивості арифметичного квадратного кореня”

Алгебра 9 клас (для спеціальної школи)

 

 

 

 

Вчитель: Біліченко Н.А.

 

 

 

 

 

 

 

 

 

м. Дніпро

 

                                                                  

Алгебра,  9 клас                                                            

 

Тема уроку: Властивості арифметичного квадратного кореня.

Мета: освітня: формування математичної компетентності (сформувати в учнів знання про властивості арифметичного квадратного кореня, сформульовані у вигляді теорем; формувати вміння застосовувати вивчені властивості для обчислення значень виразів, спрощення та перетворення виразів; формувати культуру усних та письмових обчислень);

розвиваюча: формування компетентності вміння вчитися впродовж життя (формування уміння визначати мету навчальної діяльності, відбирати й застосовувати потрібні знання та способи діяльності для досягнення цієї мети; знаходити зв’язок з раніше вивченим: переносити набуті знання в нові ситуації); стимулювання учнів до висловлювань без побоювань помилитися; формування компетентності спілкування державною мовою (формування умінь ставити запитання і розпізнавати проблему; міркувати, робити висновки; грамотно висловлюватися рідною мовою);

виховна: формування соціальної і громадянської компетентності (уміння висловлювати власну думку, слухати і чути інших, оцінювати аргументи та змінювати думку на основі доказів); формування компетентності ініціативності та підприємливості (формувати уміння вирішувати життєві проблеми, аналізувати, прогнозувати).

корекційна: розвивати зорове сприймання, корекцію пізнавальної діяльності, формування навичок просторового орієнтування; формувати компенсаторні способи діяльності шляхом максимального використання потенційних можливостей, спроможності і здібностей дитини з порушеннями зору; корегувати порушення емоційно-вольової сфери; корегувати індивідуальні прогалини в знаннях; відновлювати позитивні якості, які одержали незначну девіацію; стимулювати сенсорні функції (зорового, слухового, кінестетичного сприйняття); розвивати зорово-рухові координації і функціональні можливості кисті і пальців; накопичувати навички моральної поведінки.

 

Тип уроку: засвоєння нових знань.

Міжпредметні зв’язки: інформатика, історія.

Обладнання: мультимедійне обладнання, презентація, підручник А.Г. Мерзляк, Алгебра, засоби корекції, індивідуальні картки.

Очікувані результати: після цього уроку учні повинні

знати:

–     поняття квадратного кореня;

–     поняття арифметичного квадратного кореня;

–     властивості арифметичного квадратного кореня;

вміти розв’язувати вправи, що передбачають:

–     застосовувати поняття арифметичного квадратного кореня для обчислення значень виразів;

–     перетворення виразів із застосуванням властивостей арифметичного квадратного кореня.

Епіграф уроку:

Мало мати хороший розум, головне добре його застосовувати.

Рене Декарт

Хід уроку

 

І. Організаційний етап. (1хв)

Встаньте, діти, всі рівненько,

Посміхніться всі гарненько.

Посміхніться всі до мене.

Посміхніться і до себе.

Посміхніться до гостей.

Привітайтесь «Добрий день»

Хай в усіх гарно розпочнеться новий день!

Перевірка готовності дітей до уроку: на партах усі необхідні речі для уроку алгебри, засоби корекції: окуляри, підставки для книг.

ІІ. Мотивація навчальної діяльності. (1 хв)

1. Налаштування на урок.

-         Тож налаштуймось на урок і промовимо із заплющеними очима вислови:

-         Я – учень.

-         Я ходжу до школи.

-         Мене вчать вчитися.

-         Я все розумію.

-         Я хочу все знати.

2. Озвучування дивізу.

-         А тепер девіз згадаймо і урок наш починаймо.

Міркуємо – швидко!

Відповідаємо – правильно!

Лічимо – точно!

Пишемо – гарно!

Слайд 1 (епіграф)

 

ІІІ. Перевірка домашнього завдання. (3 хв)

 

Відповідь на запитання учнів, які виникли під час виконання домашнього завдання. Наприкінці уроку вчитель збирає зошити для перевірки домашнього завдання.

Слайд 3 (завдання на відповідність)

Слайд 4 (відповіді)

 

ІV. Повідомлення теми, мети та завдань уроку. (3 хв)

Слайд 5 (Тема уроку)

На попередніх  уроках ми вивчили поняття арифметичного квадратного кореня. Сьогодні познайомимося з властивостями арифметичного квадратного кореня, навчимося використовувати їх при обчисленні виразів, що містять квадратні корені. Отже, запишемо число, класна робота та тему уроку «Властивості арифметичного квадратного кореня».

Вам давно відомі слова відомого французького математика Рене Декарта «Мало мати хороший розум, головне добре його застосовувати». Сподіваюсь, сьогодні ми всі будемо застосовувати наш розум на повну силу.

V. Актуалізація опорних знань (5 хв)

А зараз пропоную вам невеличку розминку для нашого розуму, щоб налаштувати його на серйозну роботу. Завершіть речення:

• Квадратним коренем з невід'ємного числа а називається... (число, квадрат якого дорівнює а)

• Арифметичним квадратним коренем з невід'ємного числа а називається... (невід’ємне число, квадрат якого дорівнює а)

• Рівняння х² = а (а  0) має корені... ()

• Натуральними називаються числа ... (які використовуються при лічбі предметів)

• Цілими називаються числа... (натуральні, протилежні їм та число нуль)

• Раціональними називаються числа... (які можна подати у вигляді робу з цілим чисельником і натуральним знаменником. Раціональні числа можуть бути представлені скінченим або нескінченим періодичним десятковим дробом)

• Ірраціональними називаються числа... (нескінчені неперіодичні десяткові дроби)

• Дійсні числа — це ... (раціональні та ірраціональні числа)

2. Подумайте, обчисліть усно:

, , , , , , , .

VI. Вивчення нової теми (5 хв)

Слайд 6 (мета)

Слайд 7 (Декарт – історична довідка)

 

Знаходити значення квадратного кореня вміли вавилонські вчені ще чотири тисячі років тому. Спочатку вони складали таблиці квадратів чисел і відповідно квадратних коренів із них. У добу Відродження європейські математики корінь позначали словом «RADIX» (редис), а згодом скорочено – буквою «R». Німецькі математики ставили над числом кружечок, а згодом перед числом кружечок, пізніше  – ромбик, далі – галочку і над виразом, з якого добували корінь, риску. Потім, у XII столітті Рене Декарт поєднавши знак V з рискою, отримав . Символ  називають ще радикалом.

Фізкультхвилинка для очей (2 хв)

 

Другий  етап організації виконання плану діяльності.

VII. Сприйняття й первинне усвідомлення учнями нового матеріалу (7 хв)

Викладання нового матеріалу

 Розглянемо рівності: , . Чи згодні ви, що для будь-якого значення а виконується рівність ? Чи правильною буде рівність . Звичайно, ця рівність є неправильною, так як . Насправді, , . Отже, справедливою є така теорема:

Теорема 15.1. Для будь-якого дійсного числа а виконується рівність .

Доведення.

Для того щоб довести рівність , треба показати, що і .

Маємо: при будь-якому а. Також з означення модуля випливає, що . Отже, теорему доведено.

Наприклад, ; .

Розглянемо приклад.

Приклад. Спростіть вираз , якщо .

Розв’язання. .

Наступна теорема узагальнює доведений факт.

Теорема 15.2 (арифметичний квадратний корінь зі степеня). Для будь-якого дійсного числа а та будь-якого натурального числа n виконується рівність .

Наприклад, ; .

Теорема 15.3 (арифметичний квадратний корінь із добутку). Для будь-яких дійсних чисел a і b таких, що і , виконується рівність .

Доведення

Маємо: і . Тоді . Крім того, . Отже, вираз  набуває тільки невід’ємних значень, і його квадрат дорівнює ab.

Наприклад, .

Доведена теорема поширюється на випадок, коли кількість множників під знаком кореня більша за два.

Наприклад, , якщо .

Теорема 15.4 (арифметичний квадратний корінь із дробу). Для будь-яких дійсних чисел a і b таких, що і , виконується рівність .

Доведення цієї теореми проведіть вдома самостійно, так як воно аналогічне доведенню попередньої теореми.

Наприклад, ; .

Помінявши в тотожностях і місцями їхні ліві та праві частини, маємо: і . Цими тотожностями користуються в процесі множення й ділення арифметичних квадратних коренів.

Наприклад, ; .

2. Первинне закріплення знань.

▪ Виконання усних вправ  (4 хв)

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

є) ;

▪ Робота учнів біля дошки

1. Знайти значення виразу: № 483^•. (2 хв)

1) ;

2. Спростіть: №487^• (4 хв)

1) , якщо ;

2) , якщо ;

Фізкультхвилинка для тіла (1 хв)

 

▪ Усне опитування

Знайди помилки і поясни (1 хв)

Слайд 8

1.                     

 

2.                     

 

3.                        

 

▪ Індивідуальна робота за картками  (4 хв)

Картка № 1

1. Знайдіть значення виразу:

а) ;

б) ;

в) ;

2. Спростіть:

а) ;

б) , якщо ;

Картка № 2

1. Знайдіть значення виразу:

а) ;

б) ;

в) ;

2. Спростіть:

а) , якщо ;

б) , якщо ;

 

Перевірити й оцінити роботи учнів після уроку.

Перед здачою  самостійної роботи оцініть себе. Поставте оцінку за пророблену роботу та смайлик, що характеризує рівень засвоєння:

- відмінно

 

- добре

 

не зрозуміло мені нічого

А тепер обміняйтесь своїми роботами, звірте з розв’язками, що записані на дошці та поставте оцінку зеленою ручкою своєму сусідові по парті

VIІІ. Домашнє завдання. (1 хв)

Опрацювати §15, № 476 (1,3,5), 484, 488 (5-8)*

 

IX. Підсумок уроку. (1 хв)

- Ось і підійшов до закінчення наш урок.

- Що найбільше сподобалося на уроці?

- Хто вважає, що працював на уроці дуже гарно?

- Що ж за сюрприз чекав на вас ?

- Ви і справді розумники – впоралися з усіма завданнями, працювали дружно, старанно.

Ми розглянули одну з тем математики «Арифметичний квадратний корінь», але об’єм математичних знань безкінечний, самі математичні знання неоцінені, а області застосувань математики  безмежні.

 Тож, я впевнена, що вам математика завжди буде в нагоді.