Урок "Нерівності трикутника"

Урок геометрії у 7 класі

«Нерівності трикутника. Співвідношення між сторонами

і кутами трикутника»

Тема уроку. Нерівності трикутника. Співвідношення між сторонами і кутами трикутника

Мета:

навчальна: сформулювати теорему про співвідношення між сторонами і кутами трикутника, розуміння і засвоєння нерівності трикутника; учити застосовувати вміння, які передбачають застосування цих теорем.

 розвивальна: розвивати пізнавальний інтерес до предмета, увагу, інтелектуальні здібності учнів, уміння аналізувати та робити висновки;

виховна: виховувати почуття відповідальності, інтерес до предмета, уміння організовувати свою роботу.

формування ключових компетентностей: інформаційної, комунікативної, пізнавальної, творчої.

Тип уроку: засвоєння нових знань та вмінь.

Обладнання: проектор, набір креслярських інструментів, роздатковий матеріал, підручник.

Хід уроку

І. Організаційний етап

ІІ. Мотиваційний етап

Отже, починаємо роботу. Я хочу, щоб епіграфом нашого уроку стали такі слова «Скажи мені – я забуду. Покажи мені – я запам’ятаю. Залучи мене – я навчусь»   (східна приказка) (Слайд 2).

ІІІ. Перевірка домашнього завдання (Гра «ВПОДОБАЙКА»)   (Слайд 3).

№1  Відповідь: а) P_∆KPT  = 15 см.

                           б) P_∆KPT  = 10 дм.   

№ 425   Відповідь:100º, 80º, 100º, 80º.

ІV. Актуалізація опорних знань

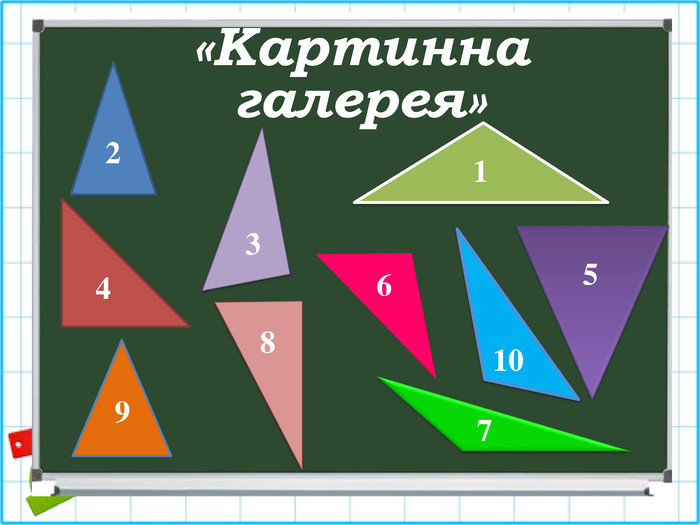
1. Метод «Картинна галерея» 

Перед  Вами картини із зображенням різних трикутників, потрібно  «розвісити» всі картини на 2 стіни за спільною ознакою.  (Слайд 4).

Ну, що ж продовжимо далі. А допоможе нам сьогодні на уроці Ваш улюблений телефон (слайд 5). Та справа в тому, що спочатку потрібно його розблокувати. Тож скористаємося сканером QR-кодів, розшифруємо дану інформацію і виконаємо необхідне завдання.

https://learningapps.org/display?v=p56tmkm1j01

Продовжимо далі.

Самостійна робота (слайд 8)

І варіант

1. Які кути називаються суміжними?

Є) кути, сторони яких є доповняльними променями;

Е) кути, на які розбивається розгорнутий кут його внутрішнім променем.

Ж) кути, які в сумі дають 180°;

2. Який трикутник називають рівнобедреним?

П) трикутник, у якого всі кути гострі;

 Р) трикутник, у якого всі сторони рівні;

С) трикутник, у якого дві сторони рівні.

3. Яка властивість вертикальних кутів?

А) вертикальні кути в сумі дають 180°;

Б) вертикальні кути рівні;

В) вертикальні кути утворюють розгорнутий кут.

4. Яка властивість кутів рівнобедреного трикутника?

І) кути при основі рівні;

К) всі кути рівні;

Л) всі кути по 60°.

5. Який трикутник називається прямокутним?

З) трикутник, у якого всі кути прямі;

І) трикутник, у якого всі сторони перпендикулярні;

К) трикутник, у якого один кут прямий.

ІІ варіант

1. Які кути називаються вертикальними?

Е) кути, сторони яких є доповняльними променями;

К) кути, на які розбивається розгорнутий кут його внутрішнім променем.

Л) кути, які рівні;

2. Як називаються сторони рівнобедреного трикутника?

Т) гіпотенуза і катети;

С) основа і бічні сторони;

У) бедра і третя сторона.

3. Яка властивість бісектриси рівнобедреного трикутника?

Г) бісектриса ділить кут на два рівні відрізки.

В) бісектриса ділить протилежну сторону навпіл; Б) бісектриса, проведена до основи, є висотою та медіаною рівнобедреного трикутника.

 4. Яка властивість внутрішніх різносторонніх кутів?

Н) ці кути в сумі дають 180°;

І) ці кути рівні;

П) утворюють розгорнутий кут.

5. Яка властивість рівнобедреного трикутника?

 К) Кути при основі рівні;

 О) Бісектриса, проведена до бічної сторони, є медіаною і висотою;

 П) Його сторони перпендикулярні між собою.

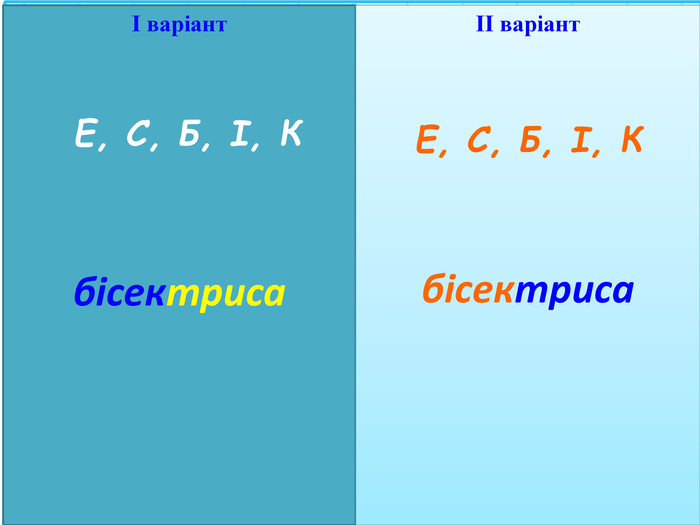
Перевіримо, що у вас вийшло: І і ІІ варіант: Е, С, Б, І, К.

Завдання: перставте букви місцями,  додайте ще п’ять букв і вийде слово, яке є елементом трикутника. (бісектриса)

V. Вивчення нового матеріалу

1) (Створення проблемної   ситуації).

 Наш телефон ми розблокували, продовжимо далі.  Ми отримали повідомлення  з інтернет-магазину   Аliexpress.

   Деякий добродій Х захотів розбагатіти і почав продавати земельні ділянки, які мають форму трикутників. Продав 3 ділянки розміри яких: 2м, 4м, 6м; 1м, 3м, 5м і 3м, 5м, 7м. Але люди, які купили перші дві ділянки, прийшли з претензіями, що таких ділянок не існує.

Як  ви думаєте? Чому виникла така ситуація? (вчитель слухає відповіді учнів, разом роблять висновок, що не всі  трикутники з такими сторонами існуватимуть).

Для того ми й будемо вивчати геометрію далі і сьогодні вивчимо тему, яку ви бачите на екрані (слайд  6). Запишіть у зошити число, класна робота, тему уроку.

2. Дослідницька робота (Слайд 7)

Завдання 1:

1) Виміряти довжини цих трубочок і скласти з них трикутник.

2) Порівняйте довжину кожної  сторони трикутника із сумою двох інших сторін.

Запитання вчителя:

• Чи справилась із своїм завданням І група? (трикутник зі сторонами 7см, 12см, 9см)   Так.
• Чи побудували трикутник зі сторонами 7см, 14см, 7см учні ІІ групи?  Ні.
• А третя група змогла побудувати трикутник зі сторонами 5см, 16см, 7см?  Ні.
• Від чого  залежить  можливість    побудови  трикутника? (Від довжин його сторін).
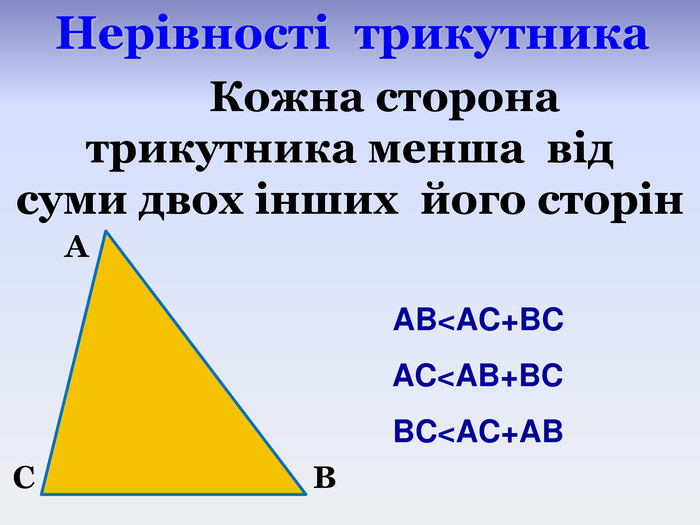
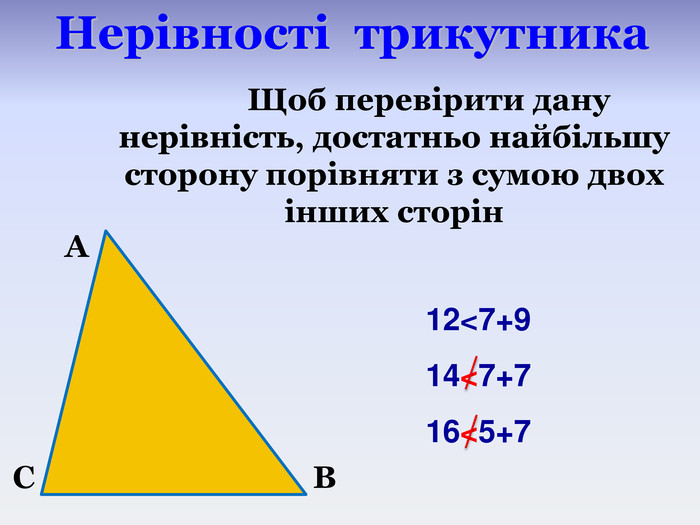
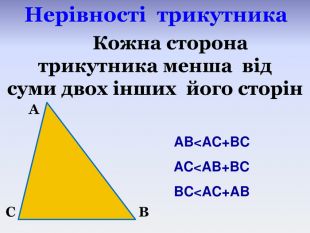
• Який висновок можна зробити? (Кожна сторона трикутника менша  від суми двох інших  його сторін). Кожну із цих трьох нерівностей називають нерівністю трикутника.
• Як ви думаєте, обов’язково перевіряти всі три сторони? Достатньо порівняти більшу сторону трикутника із сумою двох інших.

Завдання 2:

1) Виміряти довжини  сторін і кутів  трикутника.

2) Порівняти довжини сторін із мірами протилежних  до них кутів?

Який висновок ви можете зробити, провівши дане дослідження?

В трикутнику:

1) проти більшої сторони  лежить більший кут; і навпаки,  проти більшого кута

  лежить більша сторона.

VІ. Закріплення вивченого матеріалу.

Поки ви працювали, на телефон прийшло декілька повідомлень у Messenger. (слайд 20).

•   Виконання усних вправ

1. Чи існує трикутник із сторонами 2 см, 5 см, 7 см? (Ні, бо 7=2+5)
2. Чи існує рівнобедрений трикутник із бічною стороною 9 см і основою 18 см? (Ні, бо 18=9+9)
3. Периметр трикутника 20 см. Чи може одна з його сторін дорівнювати 9 м? (Так, бо на дві інші припаде 11 см, а 9<11)
4. Сторони трикутника 12,18, 8 см. Проти якої  сторони буде  найменший кут? (Проти сторони 8 см).

Фізкультхвилинка

•   Виконання письмових вправ (слайд 23).

Нам знову прийшло повідомлення у додаток «Книги». А це означає, що ми працюємо з книгою, а зокрема і нашим підручником.

 Робота з підручником : №445(1). (Коментуємо з місця)

Скористаємось малюнком 194.

∠С=180º - (45º+60º)=75º. ∠С найбільший, то найбільша сторона АВ.

Задача 1. (біля дошки) Периметр рівнобедреного трикутника 60 см, а дві його сторони відносяться як 2:5.  Знайти сторони трикутника

Розв’язання: 1) нехай бічні сторони трикутника 2х см, а основа – 5х см.

Тоді 2х+2х<5х – суперечить теоремі про нерівність трикутника.

2.            нехай бічні сторони трикутника 5х см, а основа – 2х см.

Тоді 5х+5х+2х=60

12х=60

х=60:12

х=5

5*5=25 (см) – бічна сторона;

5*2=10 (см) – основа.

Відповідь: 25 см, 25 см, 10 см.

Робота з підручником : №460  (біля дошки)

Розв’язання: Р_кв.=140 см.

140:4=35 (см) – сторона квадрата і трикутника;

210-140=70 (см) – залишиться на 2 сторони BD.

BD>AB, то BD>35, тому 210 см мережива не вистачить.

Відповідь: ні.

Задача 2 (додатково) самостійно

Петрикові потрібно обгородити грядку трикутної форми,  сторони якої відносяться як 4:5:8. Периметр ділянки 34 м. Знайти сторони ділянки.

Розв’язання: 4х+5х+8х=34

17х=34

х=34:17

х=2

4*2=8 (см)- І сторона;

5*2=10 (см)  - ІІ сторона;

8*2=16 (см) – ІІІ сторона.

Відповідь: 8, 10, 16 см.

VІІ. Підбиття підсумків уроку (слайди 24-29)

Поки ми розв’язували задачі на телефон знову надійшло повідомлення у Instagram. Давайте розшифруємо сканером QR-кодів і прочитаємо його.

Цікаві факти про трикутник

1. Трикутник - фігура, про властивості якої людство дізналось ще в VІ столітті до нашої ери. Наші предки помітили, одну цікаву властивість, яку називали жорсткість (з цим поняттям ви будете зустрічатися на уроках фізики).
2. Трикутники широко застосовуються в нашому житті. Давногрецький мислитель Платон говорив: «Все в світі складається з трикутників».
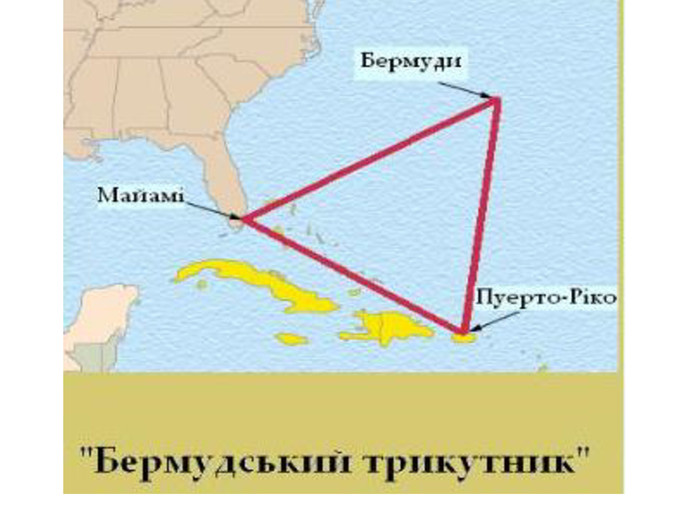
3. Бермудський трикутник – район в Атлантичному океані, в якому начебто відбуваються таємничі зникнення морських і повітряних суден.
4. Трикутник також є поширеним символом на писанках. У ньому втілена ідея триєдиності: неба, Землі, води. Цей знак також символізує батька, матір, дитину. Це символ божественної Трійці.
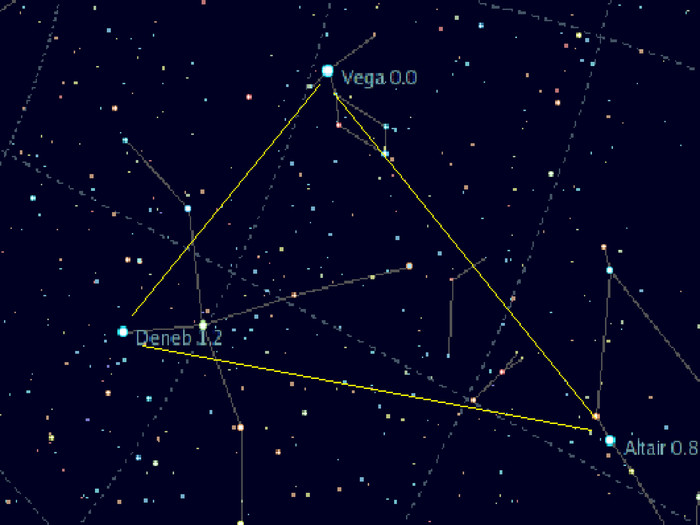
5. Лісова пташка малинівка, за свідченням орнітологів, здійснює прельоти тільки вночі. Орієнтується на великий літній трикутник на зоряному небі: Вега, Денеб, Альтаїр.

Можна наводити ще багато цікавих фактів про трикутник, але наш урок завершується.

VІІІ. Рефлексія

1. Чи цікаво було вам сьогодні на уроці?
2. Чи переконалися ви в тому, що геометрія потрібна і цікава?
3. Що нового ви навчилися сьогодні?
4. Що вам найкраще сподобалося?

ІX. Домашнє завдання

І отримайте ще повідомлення на Viber.

 Опрацювати § 15,  

Виконати №№ 446, 456.

Додаткове завдання