Урок "Основна властивість первісних"

       Тема: Основна властивість первісних. Правила  знаходження первісних.

Мета: Засвоїти основну властивість первісних, найпростіші правила   знаходження первісних та їх застосування; виховувати інтерес до математики; розвивати уміння робити висновки; створювати умови для реалізації своїх здібностей, умінь та навичок.

Тип уроку: Засвоєння нових знань.

Обладнання: таблиці первісних і невизначеного інтеграла, шаблон   параболи,  креслярські приладдя.

Хід уроку

I. Організаційний момент.

II. Перевірка домашнього завдання.

     Проглянути зошити у кращих учнів, а вони в свою чергу перевіряють домашнє    завдання у своїх товаришів.

III. Засвоєння нових знань.

       Виясняємо, яка теорема називається лемою. Кращі учні формулюють лему та    пояснюють її геометричне значення.

        Учень (по бажанню) доводить теорему 1.

             Теорема 1 Якщо на проміжку (а;б) функція F (x) є первісною для f (x), то на цьому проміжку первісною для f (x) буде також функція F (x) + С, де С – довільна стала(число).

       Другий учень доводить теорему 2.

             Теорема 2. Будь-які дві первісні для однієї і тієї самої функції відрізняються одна від одної тільки на сталий доданок.

        Якщо таких учнів, які б бажали довести теореми немає, то вчитель формулює і доводить теореми сам, а учні повторюють їх.

             Геометричний зміст основної властивості первісної: Якщо відомий графік однієї з первісних у = F (x) для даної функції у = f (x), то графіки інших первісних у = F (x) + С для цієї самої функції можна побудувати  паралельним перенесенням відомого графіка вздовж осі ординат на С одиниць.

         Приклад:

           Нехай F (x) = х² + С, то

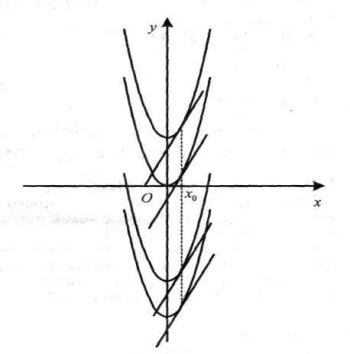
       Тому, що операція знаходження первісних (інтегрування) обернена до операції диференціювання (знаходження похідних), то правила знаходження первісних випливають із правил знаходження похідних, тобто:

        1) Якщо F (x) є первісною для  f (x), а G (x) є первісною для g(x), то

             F (x) + G (x) –  є первісною для f (x) + g(x).

        2) Якщо F (x) є первісною для  f (x), а k – стале число, то k F (x) є первісною для          k f (x).

        3) Якщо F (x) є первісною для  f (x), а k і в – сталі, причому k ≠ 0, то

            (1∕ k) F (k x + в) є первісною для f(k x + в).

        Приклад 1:

             Знайти загальний вигляд первісної функції     х² + (¹∕_х²)

        Розв’язання:  f (x) = х² + (¹∕_х²) оскільки дана функція є сумою функцій х² і (¹∕_х²), то за першим правилом F (x)=( х³ ∕ 3) – (1  ∕ х)+ С.

       Приклад 2: 

                f(x) = 2х³ – sin х

       Розв’язання: використовуючи друге правило і перше, маємо:

               F (x) = (2х⁴  ∕ 4) + cos x + С.

        Приклад 3:

              F (x) = 1 ∕ √(7х+2)

       Розв’язання: оскільки функція f (x) складена (корінь добувають із функції), то за третім правилом   F (x) = (2√( 7х + 2) ∕ 7) + С .

       Приклад 4:

               Для даної функції  f (x) =6 х – х⁴ знайти первісну, графік якої проходить через точку М(1;2).

       Розв’язання: Знайдемо загальний вигляд первісної: F (x) = (6х²  ∕ 2) – (х⁵∕ 5) + С, якщо графік первісної проходить через точку М(1;2), то F (x) = 2, а х₀ = 1, тому 2 =( 6∙1² ∕ 2) – (1⁵∕ 5) + С, тобто 2 = 3 – (1 ∕ 5) + С ; 2 = 2,8 + С.

         Звідси С = 2 – 2,8 = - 0,8.

                Отже та первісна функції f (x), графік якої проходить через точку М(1;2) має вигляд :         F (x) = 3х² – (х⁵ ∕ 5) – 0,8.             

IV. Домашнє завдання.

      Повторити § 21,22.

      Опрацювати § 23.

      Розв’язати № 56 (6,7).