Тема. Ознака подібності трикутників за двома сторонами                                     і кутом між ними

Мета: розширити знання учнів про подібність; вивчити ознаку

подібності за двома сторонами і кутом між ними; формувати навики розв’язування задач, використовуючи ознаки подібності; вчити логічно мислити.

 Тип уроку: засвоєння нових знань, умінь.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Перевірка правильності виконання домашнього завдання шляхом пояснення розв’язання по заздалегідь підготовленим рисунком.

 ІІІ. Актуалізація опорних знань та вмінь

Виконання усних вправ

1. Два подібні трикутники мають спільний кут. Чи обов’язково їх сторони, протилежні цьому куту паралельні?

2. Знайдіть АВ вибравши вірні етапи рішення задачі.

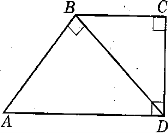
      І.  1) ∆АВD ~ ∆ВСD; 2) ∆ВАD ~ ∆ВСD;

         3)  ∆АВD ~  ∆DСВ.

      ІІ   1) = ; 2) = ; 3) = .

     ІІІ  1) х = 2; 2) х = ; 3) х = 2.

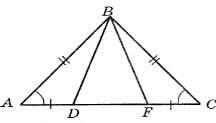
3.  Доведіть, що ∆ВDF – рівнобедрений.

ІV. Формулювання мети і завдань уроку

Продовжимо вивчати ознаки подібності – подібність трикутників за двома сторонами і кутом між ними.

V. Сприйняття та усвідомлення нового матеріалу

Проведемо ще одну аналогію між рівністю і подібністю трикутників.

   І ознака рівності                                ІІ ознака подібності

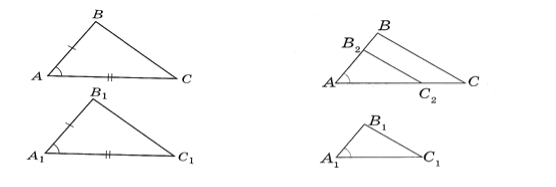
ЯкщоА =А₁, АС = А₁С₁ і          Якщо А =А₁ і = , АВ = то  ∆АВС = ∆А₁В₁С₁.                         = А₁В₁, то ∆АВС ~ ∆А₁В₁С₁.

    Деяка аналогія існує.                        

Теорема (друга ознака подібності: за двома сторонами і кутом між ними). Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники подібні.

Доведення.

Нехай дано ∆АВС і ∆А₁В₁С₁, в яких А =А₁ і = . Доведемо, що ∆АВС ~ ∆А₁В₁С₁.

Відкладемо на промені АВ відрізок АВ₂ = А₁В₁ і проведемо пряму В₂С₂ || ВС. Тоді  АВС = АВ₂С₂   як  відповідні  кути  при  паралельних  прямих,  тому  ∆АВ₂С₂ ~ ∆АВС за двома кутами. Звідси = , а оскільки АВ₂ = А₁В₁  і  = ,  то  А₁С₁ = АС₂.   Тоді ∆АВ₂С₂ =  ∆А₁В₁С₁ за першою ознакою рівності трикутників і А₁В₁С₁ = АВС = АВ₂С₂. Отже, ∆АВС ~ ∆А₁В₁С₁ за двома кутами.

VІ. Закріплення та осмислення нового матеріал

Виконання усних вправ

1. Знайдіть подібні трикутники і доведіть їх подібність.

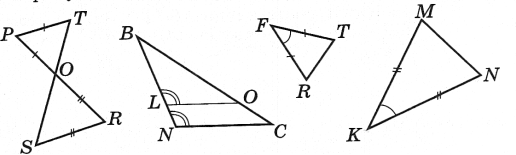
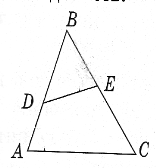2.

Дано: = = 2, DЕ = 5,5см.

Знайти: АС.

Виконання письмових вправ

№1. Діагоналі чотирикутника АВСD перетинаються в точці О. Відомо, що АО : ОС = ВО : ОD. Доведіть, що АВСD  – трапеція або паралелограм.

№2. Відрізки АВ  і СМ  перетинаються  в точці О, АО = 24см, ВО = = 16см, СО = 15см, ОМ = 10см, АОС = 74º. Знайдіть ВМО.

№3. У трикутниках АВС і А₁В₁С₁ А = А₁, кожна із сторін АВ і АС становить 0,6 сторони А₁В₁ і А₁С₁ відповідно. Знайдіть сторони ВС і В₁С₁, якщо їх сума дорівнює 48см.

№4. Доведіть, що в подібних трикутниках медіани, проведені з вершин відповідних кутів, відносяться як відповідні сторони.

VІІ. Підсумки уроку

Запитання.

1. Сформулюйте ознаку подібності трикутників за двома сторонами і ку­том між ними.

2. Чи обов’язково два подібні трикутники рівні, якщо рівні дві їхні сторони?

3. Чи подібні рівнобедрені трикутники, якщо вони мають:  1)  по рівному гострому куту; 2) по рівному тупому куту?

 VІІІ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять.

№5. У трикутниках АВС і МКН В = К, а кожна із сторін АВ і ВС у 2,5 раза більша за сторони МК і КН відповідно. Знайти сторони АС і МН, якщо їх різниця дорівнює 30см.

№6. Діагоналі трапеції АВСD точкою перетину  діляться у відношенні 3 : 7. Знайдіть основи трапеції, якщо її середня лінія 10см.