Тема. Ознака подібності трикутників за трьома сторонами

Мета: довести  ознаку подібності трикутників за трьома сторонами; сприяти усвідомленню матеріалу, що вивчається; формувати первинні вміння відтворювати зміст теореми, записувати до умов практичних задач; розвивати дослідницькі навики.

Тип уроку: засвоєння нових знань, умінь.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Перевірка правильності виконання домашнього завдання шляхом пояснення розв’язання по заздалегідь підготовленим рисунком.

ІІІ. Формування мети і завдань уроку, мотивація навчальної діяльності

Уявимо собі дві рейки, в яких два кінці скріплено цвяхом. Зрушуючи або розсовуючи вільні кінці рейок, ми можемо міняти кут між ними.

Тепер візьмемо ще одну рейку і скріпимо її кінці з вільними  кінцями перших двох рейок.

Отримана конструкція  – трикутник  – буде жорсткою, тобто в ній не можна зрушити або розсунути жодні дві сторони, не можна змінити жоден кут. Дійсно, якби це вдалося, то ми отримали б новий трикутник, не рівний початковому. Але це неможливо за третьою ознакою рівності трикутників.

Ця властивість – жорсткість трикутників – багато використовується на практиці при будівництві залізних конструкцій (залізничний міст, кронштейн, високовольтні лінії…)

Нам вона теж допоможе при вивченні ознаки подібності за трьома сторонами.

ІV. Актуалізація опорних знань та вмінь

Виконання усних вправ

1. Сформулювати третю ознаку рівності трикутників.

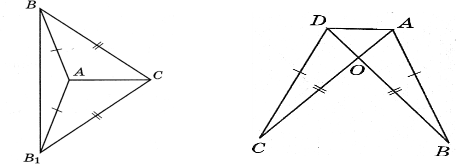2. Доведіть рівність трикутників.

Виконання письмових вправ

№1. Основи трапеції 18см і 8см. Діагональ ділить трапецію на два подібних трикутника. Знайти довжину діагоналі.

№2. Два кути одного трикутника дорівнюють двом кутам другого трикутника. Сторони першого трикутника відносяться, як 5 : 6 : 7. Знайдіть сторони другого, якщо його периметр 90 см.

V.Сприйняття та усвідомлення нового матеріалу

Практична робота

1. Побудуйте трикутник АВС і КМЕ за трьома сторонами так, щоб АВ = 2КМ;     ВС = 2МЕ; АС = 2СЕ.

2. Виміряйте кути трикутників АВС і КМЕ. Зробіть висновок.

Теорема (ознака подібності за трьома сторонами). Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники подібні).

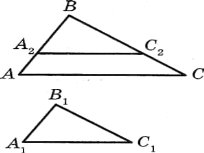Доведення.

    Розглянемо ∆АВС і ∆А₁В₁С₁, у яких =

   = = = k. Доведемо, що ∆АВС ~

        ~ ∆А₁В₁С₁.

На сторонах ВА і ВС позначимо відповідно точки А₂ і С₂ такі, що ВА₂ = В₁А₁, ВС₂ = В₁С₁. Тоді =  = k. Звідси отримуємо, що А₂С₂ || АС ( це було встановлено під час доведення другої ознаки). Отже, за лемою ∆АВС ~ ∆А₂ВС₂ з коефіцієнтом подібності k. Тоді = k, але за умовою = k. Звідси А₁С₁ = А₂С₂. Отже, ∆А₂ВС₂ = ∆А₁В₁С₁ за третьою ознакою рівності трикутників.  Так як ∆А₂ВС₂ ~ ∆АВС, то отримуємо:  ∆АВС ~ ∆А₁В₁С₁.

VІ. Закріплення та осмислення нового матеріал

Виконання усних вправ

1. В трикутниках АВС і МКН сторони пропорційні і АВ : МН =          = ВС : КН = АС :  МК. Назвіть кут трикутника МКН, що дорівнює куту С. Чому ці кути рівні?

2. Чи подібні трикутники, якщо сторони одного відносяться як           3 : 8 : 9, а сторони другого дорівнюють  24см, 9см, 27см.

Виконання письмових вправ

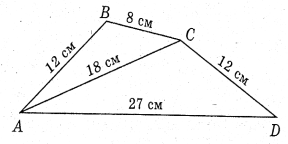№3. Знайдіть подібні трикутники на рисунку і доведіть їх подібність.

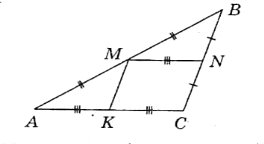    1)                                                   2)                                                                                                                                             

№4. У чотирикутнику АВСD АВ = 10см, ВС = 14см, СD = 18см, АD = 22см. Діагональ дорівнює середньому арифметичному сторін АВ і СD. Чи подібні трикутники, на які чотирикутник поділила діагональ?

№5. У чотирикутнику АВСD АD = 6см, АВ = 12см, ВС = 8см, АС = = 18см. Точка К – середина відрізка АС, DК = 4см. Доведіть, що АС – бісектриса кута трикутника DАВ.

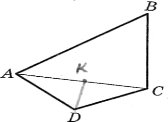Розв’язання.

   Розглянемо  ∆DАК і  ∆АВС.  В трикутниках =  = ; = = ; = = . Тоді ∆DАК ~  ∆АВС за трьома сторонами. Звідси ВАС = КАD. Отже, АС – бісектриса ∆DАВ.

VІІ. Підсумки уроку

Запитання.

1. Сформулюйте ознаки подібності трикутників.

2. Сформулюйте ознаки подібності прямокутних трикутників.

3.Сформулюйте ознаки подібності рівнобедрених трикутників.

VІІІ. Домашнє завдання

Вивчити зміст засвоєних на уроці понять та повторити раніше вивчений матеріал теми «Подібність трикутників».

№1. Доведіть, що середини сторін трикутника є вершинами подібного йому трикутника, використовуючи різні ознаки подібності.

№2. В  трикутнику АВС знайдіть сторону АС,  якщо АВ =  = 4см,  а точка D належить стороні ВС, причому ВD = 1см, DC = 15см, АD = 3,5см.