Тема.  Розв’язування нестандартних задач на ознаки подібності трикутників

Мета: виробляти практичні уміння і навички розв’язування задач на подібність ; розвивати логічне мислення, просторову уяву, вміння долати труднощі, аналізувати, творчі здібності школярів, виховувати охайність у ведені записів.

Тип уроку: застосування знань, умінь і навичок.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Домашнє завдання перевіряється за допомогою кросворда.

Кросворд.

1. Якщо два  ... одного трикутника відповідно рівні двом ... іншого трикутника, то такі трикутники подібні.
2. Два трикутники називаються подібними, якщо їх кути відповідно рівні і сторони одного трикутника  …  сторонам іншого.

3. Середня лінія трикутника …одній з його сторін і дорівнює половині цієї сторони.

4. Відношення периметрів подібних трикутників дорівнює … подібності.

Якщо ви правильно відповіли на запитання, то у виділених клітках прочитаєте назву геометричної фігури.

ІІІ. Формулювання мети і завдань уроку

На сьогоднішньому уроці мова піде про коло і подібність в нестандартних задачах.

ІV. Формування вмінь, навичок

№1. З точки S поза колом проведено січні SВ і SВ₁. Вони вдруге перетинають коло у точках А і А₁. Довести, що трикутники SАА₁ і SВВ₁ подібні.

Доведення.

   За доведенням SА · SВ = SА₁ · SВ₁. Тоді SА : SА₁ =  SВ₁ : SВ_. Оскільки у ∆SАА₁ і ∆SВВ₁ С спільний, то  ∆SАА₁ ~ ~ ∆SВВ₁ за двома сторонами і ку­том між ними.

№2. Відрізки AB і CD перетинаються в точці Е. Відомо, що         АE · ЕВ = DE · EC. Довести, що точки A, B, C, D  належать колу.                                                                                                                              

Доведення.

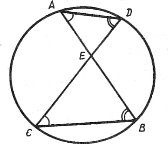Оскільки АЕ · ЕВ = DE · ЕС, то АЕ : EC =       = ED : EB. Враховуючи, що АЕD = ВЕС як вертикальні, то  ∆АЕD ~ ∆ВЕС за двома сторонами і ку­том між ними. Тоді DAE =         = ВСЕ, а це значить, що вони спираються на одну дугу. Отже, точки А, B, C, D належать одному колу.                  

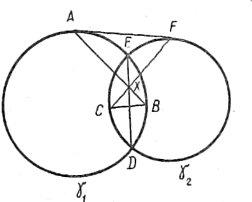
№3. Кола γ₁ i γ₂ перетинаються. На спільній хорді взято довільну точку Х і через цю точку в кругах проведено хорди АВ і СF. Довести, що трикутники AXF і BXC подібні.

Доведення.

    В колі γ₁ АХ · ХВ = ЕХ · XD за властивістю хорд, які перетинаються. Аналогічно у  колі γ₂  XF · CX = EX · XD.  Отже,  AX · XB = FX · CX, або AX : CX = = XF : XB. Враховуючи, що  AXF =     = BXC як вертикальні та останню пропорцію ∆AXF ~ ∆BXC за двома сторонами і ку­том між ними_.

― Особливо непростими бувають задачі, в яких подібність трикутників важко виявити. Тому їх називають «задачі зі схованою подібністю».

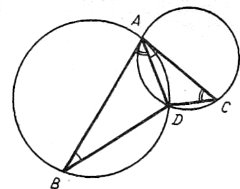
№4. Два кола перетинаються, AD — їх спільна хорда, AB i AC – хорди, які дотикаються до кожного з кіл. Довести, що AB² : AC²  =     = BD : DC. 

                              Доведення.                                                                                                                                                  Оскільки CAD =ABC так як спираються на одну хорду, aBAD = ACD за властивістю кута між дотичною і хордою, то ∆ABD ~ ∆ADC за двома кутами. Отже, AD : DC = AB : AC; BD : AD =AB : AC. Помноживши ці дві рівності,  дістанемо  BD : DC =  AB² :  AC² .

№5.  В трапеції АВСD ( АВ || СD ), АВ = а,  СD = b ( а < b). Коло, яке проходить через вершини А, В, С дотикається до сторони АD. Знайти діагональ АС.

Розв’язання.

На рисунку DАВ = АВС за властивістю кута між дотичною і хордою, а ВАС =АСD як внутрішні різносторонні. ∆ABС ~ ∆СAD за двома кутами.  Отже,     АВ : АС = АС : DС. Звідси АС² = АВ · DС; АС = = .

    Відповідь: .

№6. Точки А, В і М належать одному колу. Відстань від точки М до прямих, які дотичні до кола в точках А і В, відповідно рівні а і b. Знайти відстань від точки М до прямої АВ.

Розв’язання.

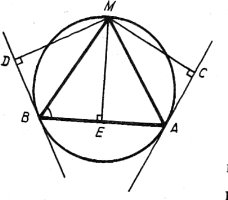Проведемо відрізки MC i MD перпендикулярно до прямих, які дотикаються до кола відповідно у точках А і В, і МЕ АВ.  За умовою МС = а і МD = b. Оскільки АВМ = САМ, то прямокутні трикутники ВМЕ і АМС подібні, і або МЕ = Аналогічно, з подібності трикутників АМЕ і ВDМ випливає МЕ =   Помножимо обидва вирази, маємо: МЕ² =     = МС · DM, або МЕ² = а · b, МЕ = Отже, шукана відстань дорівнює

Відповідь: .

V. Підсумки уроку

Запитання.

2. Які пропуски в знаннях по даній темі ви ще не ліквідували?

VІІІ. Домашнє завдання

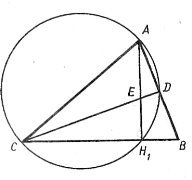
№1. Через середину Е висоти АН₁ трикутника АВС і через його вершину С проведено пряму, яка перетинає сторону АВ в точці D, причому відрізок АЕ є середнім геометричним відрізків ЕС і ED. Довести, що точки А, D, H₁ і C належать колу.

                                 Доведення.

Доведемо, що СD – висота ∆АВС.

Оскільки АЕ : CE = ED : AE = ED : EH₁ і AED =H₁EC як вертикальні, то ∆АЕD ~    ~ ∆CEH₁ за двома сторонами і ку­том між ними_. Але АН₁С = = 90º. Тоді СDA = 90º і СD – висота ∆АВС, а це значить, що точки А, D, H₁, C належать колу з діаметром  АС.

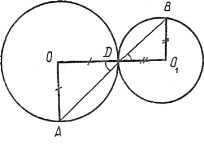
№2. Два кола з центрами О і О₁ дотикаються в точці D. Пряма, що проходить через точку D, перетинає кола у точках А і В. Довести, що трикутники АОD і DО₁В подібні.

Розв’язання.

Розглянемо випадок зовнішнього дотику кіл. Оскільки ОАD i O₁DB як вертикальні  і ∆AOD i ∆DO₁B рівнобедрені, то ці трикутники подібні за двома кутами.