Урок "Паралельність прямих і площин у просторі"

Про матеріал

Урок узагальнення та систематизації знань з теми "Паралельність прямих і площин у просторі"

Перегляд файлу

Тема. Паралельність прямих і площин у просторі

Мета: навчаюча: узагальнити, систематизувати і поглибити знання учнів з

теми «Паралельність прямих і площин у просторі», закріпити вміння

застосовувати властивості паралельних прямих і площин під час

розв’язування задач;

розвиваюча: розвивати просторову уяву учнів, математичну мову,

логічне мислення; формувати організаційну, соціально-особистісну,

інформаційну компетентності;

виховна: виховувати прагнення до знань, інтерес до математики,

показати важливість математичних знань у повсякденному житті;

виховувати почуття взаємодопомоги, взаємопідтримки, показати зв’язок

математики з іншими навчальними предметами.

Тип уроку: узагальнення та систематизація знань

Обладнання: Мультимедійна презентація, комп’ютери, мультимедійний

проектор, картки «Геометричне лото»

Очікувані результати: після цього уроку учні повинні

знати:

означення, ознаки та властивості паралельних прямих і площин, зокрема

паралельність прямої та площини; двох площин.

уміти:

розв’язувати задачі з використанням означення, ознак та властивостей

паралельних прямих і площин.

Хід уроку

І. Організаційний етап

Перевірка готовності учнів до уроку.

Навчання, невід’ємна частина нашого життя. Про це дуже вдало сказав видатний український письменник та поет Іван Франко: «Вчитися, діти мої любі, треба далі і далі, раз у раз, весь вік».

ІІ. Перевірка домашнього завдання

Педагогічний прийом «Встав пропуски»

На дошці записаний розв’язок задачі, частина якого пропущена. Завданням для учнів є заповнити пропуски.

а b Нехай α || β, а  b = C, a  α = A, a  β = B,

•C b  α = A₁, b  β = B₁. AC:BC = 1:3, BB₁ = 9 см

Знайти АА₁.

Розглянемо ∆ АА₁С і ∆ВВ₁С. С – спільний.

A₁A (ВВ₁А₁А)  α = AА₁, (ВВ₁А₁А)  β = ВВ₁,

α АА₁|| ВВ₁– за 1-ою вл. паралельних площин.

СА₁А =  СВ₁В – як відповідні кути при

АА₁|| ВВ₁ та січній СВ₁.

∆ АА₁С  ∆ВВ₁С – за двома кутами.

B₁ B = ; = ; AA₁ = = 3 (см)

ІІІ. Мотивація навчальної діяльності

Сьогодні ми закінчуємо вивчати тему «Паралельність прямих і площин у просторі». Протягом уроку повторимо теоретичний матеріал та закріпимо практичні навички у розв’язуванні задач. Але перед цим я ще раз хочу вас переконати в необхідності математичних знань в житті людини.

Чи звертали ви увагу на те, де можна побачити паралельність прямих і площин у професіях та житті людини? Як це виглядає?

Кухар-кондитер – нарізання продуктів, виготовлення тортів та багатошарового желе; будівельник – протилежні грані цегли, кладка цегляної стіни, укладання плитки, підлога та стеля кімнати; оформлення навчальних кабінетів та приватних будинків – поверхня парт і підлога, поверхня парт і стеля, полички на стіні, сходи; дошки на пилорамі; склопакети на вікнах; іграшки та ін.

До вашої уваги відеофільм «Паралельність прямих і площин у професіях».

ІV. Актуалізація опорних знань

Щоб звести в систему теоретичні знання учнів, використаємо педагогічний прийом «Геометричне лото» (робота в групах).

Кожна група отримує комплект карток. На одних є початок, на інших – продовження або закінчення твердження. Необхідно підібрати пари відповідних карток. Потім перевертаємо їх. Якщо пари складені правильно, ми отримуємо малюнок (Додаток 1).

Картка 1

1. Дві площини називаються паралельними,

якщо вони не мають спільних точок

Картка 2

2. Якщо дві прямі, які перетинаються і лежать в одній площині, паралельні

двом прямим, що перетинаються другої площини, то такі площини паралельні

Картка 3

3. Паралельні площини перетинаються січною

площиною по паралельних прямих

Картка 4

4. Паралельні площини, перетинаючи паралельні прямі,

відтинають від них рівні відрізки

Картка 5

5. Пряма, що перетинає одну з двох

паралельних площин, перетинає і другу площину

Картка 6

6. Площина, яка перетинає одну з двох паралельних прямих

перетинає і другу пряму

Картка 7

7. Через точку поза даною площиною можна

провести площину, паралельну заданій, причому тільки одну

Картка 8

8. Існує три способи розташування прямої і площини:

пряма належить площині, пряма перетинає площину, пряма і площина паралельні

Картка 9

9. Якщо пряма, що не лежить у площині паралельна якій-небудь прямій цієї площини,

то вона паралельна і самій площині

V. Узагальнення набутих знань

1. Усний рахунок

Ми повторили визначення та основні теореми. А який вони мають вигляд, нам допоможе пригадати наступне завдання. Перед вами малюнки.

1. 2.

3. 4.

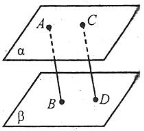
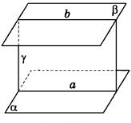
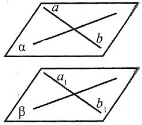
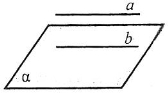
На якому з малюнків подана ілюстрація до ознаки паралельності прямої та площини?
На якому з малюнків подана ілюстрація до ознаки паралельності площин?
На якому з малюнків подана ілюстрація до властивості паралельних площин?

2. Заповнити таблицю

До вашої уваги зображення прямокутного паралелепіпеда АВСDA₁B₁C₁D₁.

За малюнком заповнити таблицю.

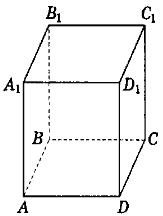
Пряма СС₁ і (A₁D₁D)

Пряма ВD₁ і (АВС)

Площини

(АВ₁В) і (ВВ₁С₁)

Площини

(АВС) і (А₁В₁С₁)

Взаємне розміщення

паралельні

перетинаються

паралельні

Хвилина відпочинку

На жаль, ні для кого не є таємницею, що для багатьох учнів математика є складним, незрозумілим, «сухим» предметом, який викликає неприйняття та нелюбов.

Що ж робити? Очевидно варто зацікавити навчальним матеріалом, намагатися, щоб він був не тільки науковим, а й пізнавальним, пов’язаним із іншими навчальними предметами.

Література та математика… Здається, дисципліни несумісні. Перша – легка, емоційна, духовна, друга – серйозна, абстрактна та досконала. Проте чи означає це те, що на уроках літератури не знайдеться місця для математики, і навпаки?

Письменники вміють бачити навколишній світ і образно описувати їх. У багатьох творах ми зустрічаємося з різними математичними явищами, термінами, твердженнями крізь призму художньої уяви авторів. До вашої уваги уривки деяких із них.

…Щоб досягти багатства, Ежен вирішив закласти дві паралельні траншеї: використати і любов, і науку, стати світською людиною і доктором юридичних наук… Ці дві лінії є асимптотами, які ніколи не зможуть перетнутися…

(Оноре де Бальзак «Батько Горіо»)

…Коли ти бачиш щось здалеку і не розумієш що це таке, спершу ти ствердиш, що це просторове тіло.

(Умберто Еко «Ім’я троянди»)

…Пролунав такий звук, якого я вжитті не чув… І, мабуть, сто років пройшло, коли я зрозумів, що сталося: Галка наштовхнулася на край гігантської піраміди. Тієї самої, яку мені старий показував минулого року. Вона з порожніх склянок.

П’ятдесят років він п’є це молоко. Дві-три склянки в день. Проста арифметика – скільки склянок? І всю цю піраміду ми зруйнували…

(Кір Буличов «Врятуйте Галю»)

…Дік жадібно поглинав знання…, він чекав, коли виросте і почне вивчати ту частину математики, яка стосується навігації.

(Жуль Верн «П’ятнадцятирічний капітан»)

…Був полудень, і слуга приніс обід, який складався тільки з одного величезного шматка телятини, який лежав на тарілці приблизно 24 фути в діаметрі.

(Джонатан Свіфт «Мандри Гуллівера»)

Також і серед поезій є такі твори.

Ті, що народжуються раз на століття,
Умерти можуть кожен день.
Кулі примхливі, як дівчата,
Вибирають найкращих.

Підлість послідовна, як геометрія,
Вибирає найчесніших.
В’язниці гостинні, як могили,
Вибирають вільних.

Криваві жоржини ростуть
над шляхом у вічність.
Тріпочуть під вітром
короткі обривки життя.
І тільки подвиг людського духу
Доточить їх до безсмертя.

Ліна Костенко

Кожний вірш Ліни Костенко – це неповторне творіння, досконале поєднання душі і розуму. Вона описує життя з його складностями, цінностями, хвилюваннями і пошуками, намагається знайти істину. Теми дуже різноманітні, але їх поєднує цілісність, насиченість, гармонійність. Та головне – правдивість.

Чорна коробочка,

Зелені оченята,

Клавішів рядочки –

Мій калькулятор.

Синус і тангенс,

Степінь і корінь,

Площі, об’єми –

Все він поборе.

Пуск! – й за хвилину

Буде готовий

Ряд інтегралів,

Дріб ланцюговий.

Пуск! – і готова

Границя складна.

Визначник, функція

Плюс похідна…

Ой ти ж, коробочко

Арифметична –

Ти геніальна

І симпатична!

Б. Олійник

Будь-яка творчість захоплює, надихає. Так, творчістю на уроках математики, є вміння розв’язувати задачі.

3. Розв’язати задачу

1. Дано паралелограм АВСD. Площина α проходить через його вершини А і В та не проходить через вершину С. Як розміщена пряма СD відносно площини α?

D C АВ  α, С  α.

CD || AB – як протилежні сторони

паралелограма.

Отже, якщо DC || AB, АВ  α то

А В CD || α за ознакою паралельності

α прямої і площини.

2. Площина α перетинає непаралельні сторони АВ і СD трапеції АВСD в точках відповідно М і N так, що АМ = ВМ, CN = ND. Як розміщені основи трапеції відносно площини α?

3. Точка С лежить між паралельними площинами α і β. Через точку С проведено прямі а і b, що перетинають площину α в точках А і А₁, а площину β в точках В і В₁ відповідно. Знайдіть АА₁, якщо АС = 3 см, В₁В = 12 см, АА₁ = СВ.

a b

А А₁

β В₁ В

Нехай α || β, а  b = C, a  α = A, a  β = B,

b  α = A₁, b  β = B₁. AC = 3см, B₁B = 12 см, АА₁ = СВ.

Знайти АА₁.

Розглянемо ∆ АА₁С і ∆ВВ₁С. АСА₁ = ВСВ₁ – як вертикальні.

(ВВ₁АА₁)  α = AА₁, (ВВ₁АА₁)  β = ВВ₁,

АА₁|| ВВ₁– за 1-ою властивістю паралельних площин.

СА₁А =  СВ₁В – як відповідні кути при АА₁|| ВВ₁ та січній А₁В₁.

∆ АА₁С  ∆ВВ₁С – за двома кутами.

AA₁  CB = 12  3

= 36

= 6 (см)

VІ. Підсумок уроку

Протягом уроку ми використовували багато понять та тверджень. Які іменники були серед них? (Площина, пряма, точка, трапеція, трикутник, паралелограм)

Пропоную вам скласти до даних слів синквейни, за допомогою яких ми узагальнимо розглянутий на уроці матеріал.

VІІ. Домашнє завдання

1. Скласти синквейн «Стереометрія».

2. §25 – 26, № 962