Урок "Паралелограм. Його ознаки та властивості"
Про матеріал
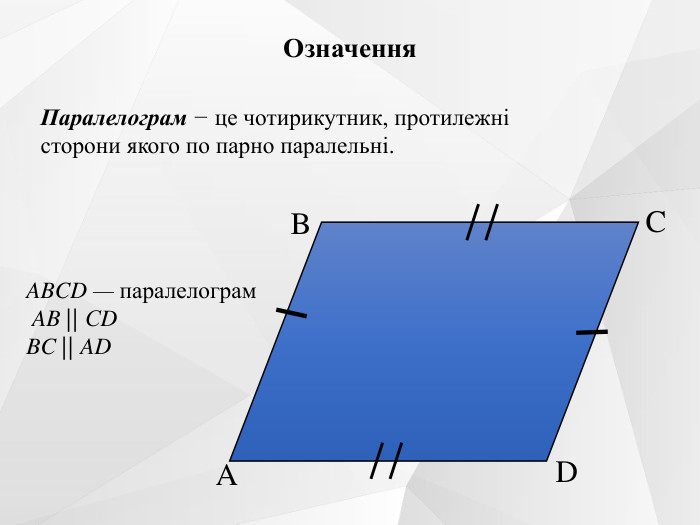
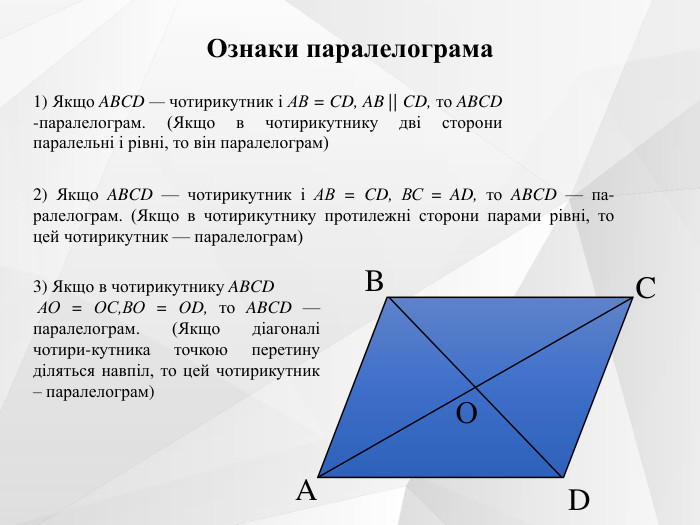
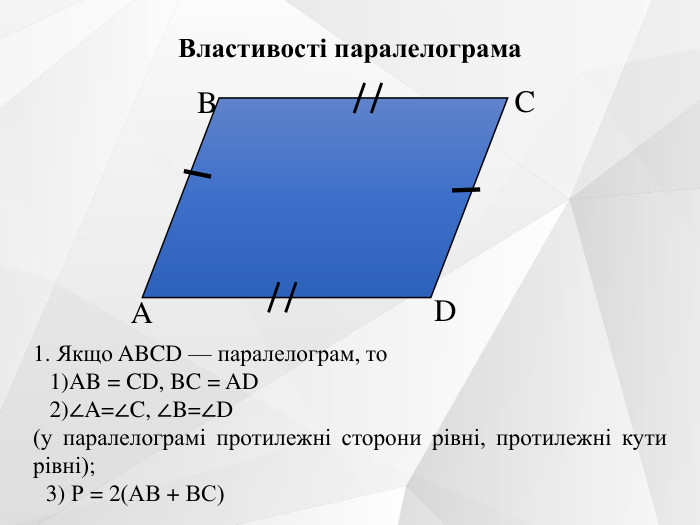
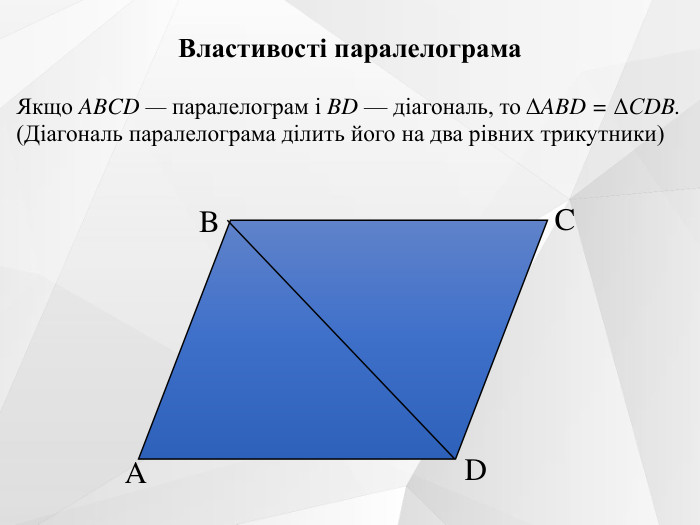
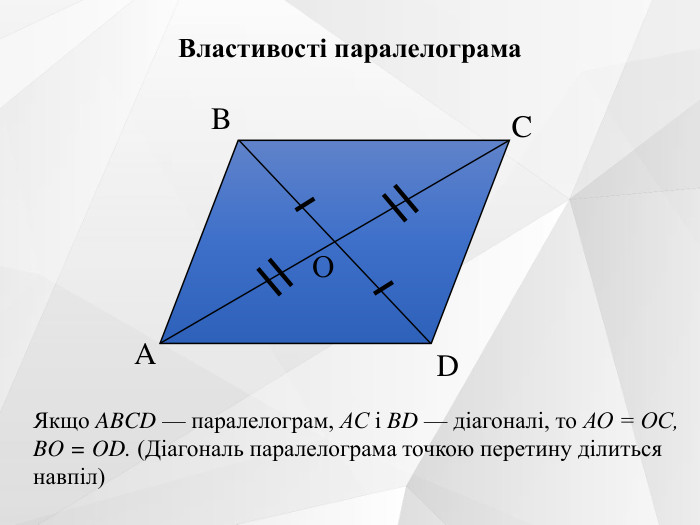
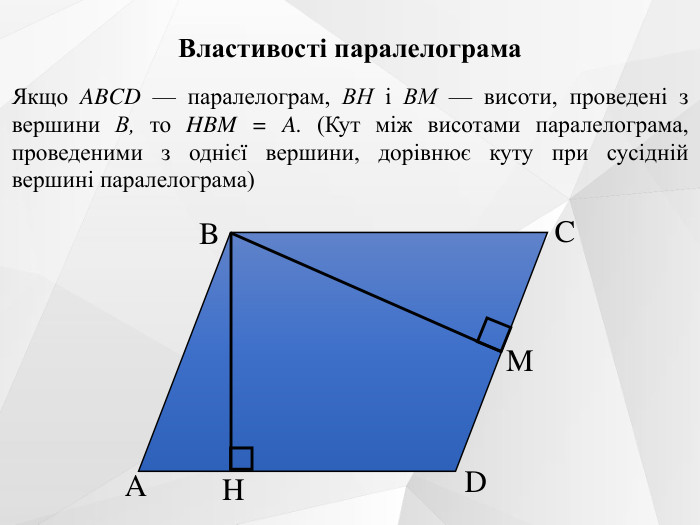
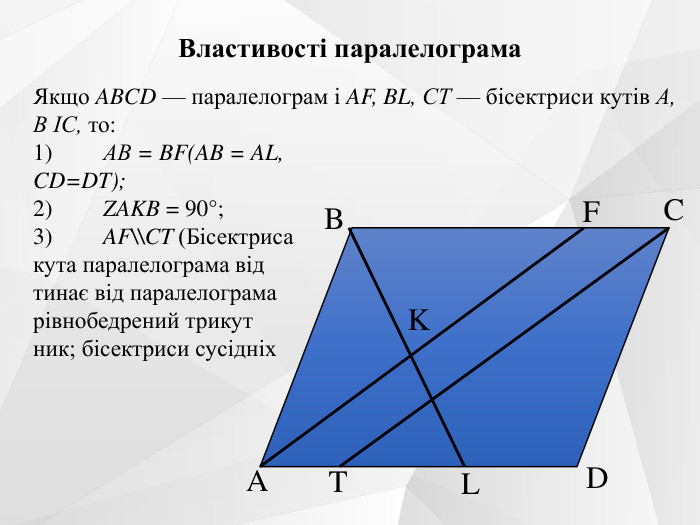
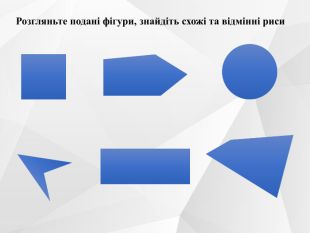
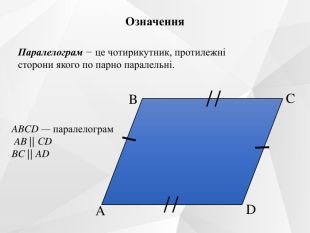
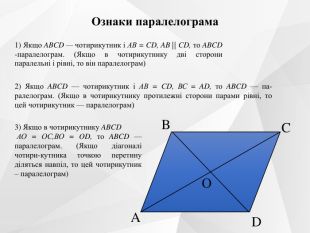
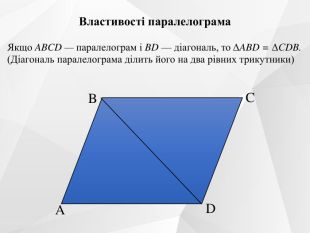
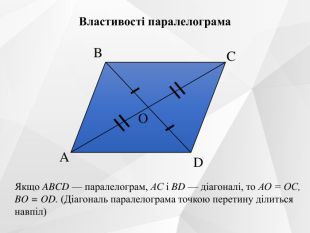
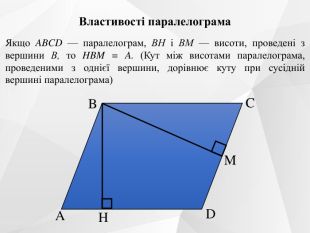
Презентація до уроку на тему "Паралелограм. Його ознаки та властивості".
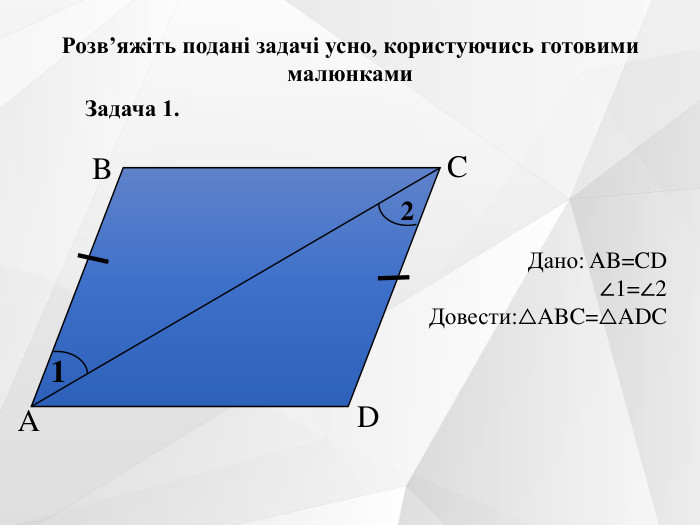
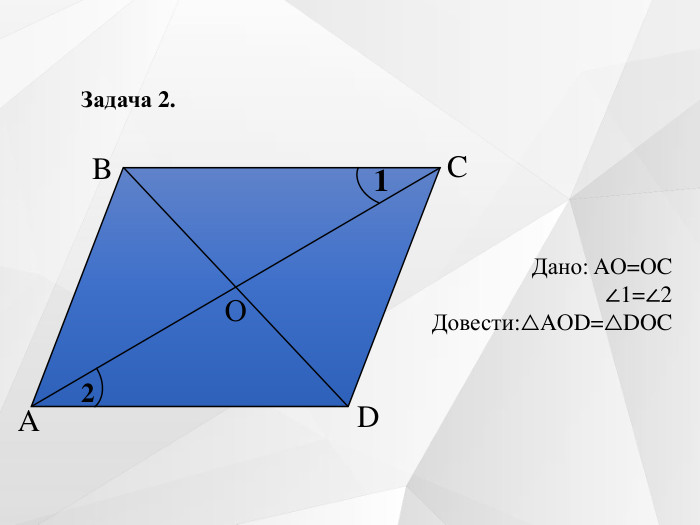
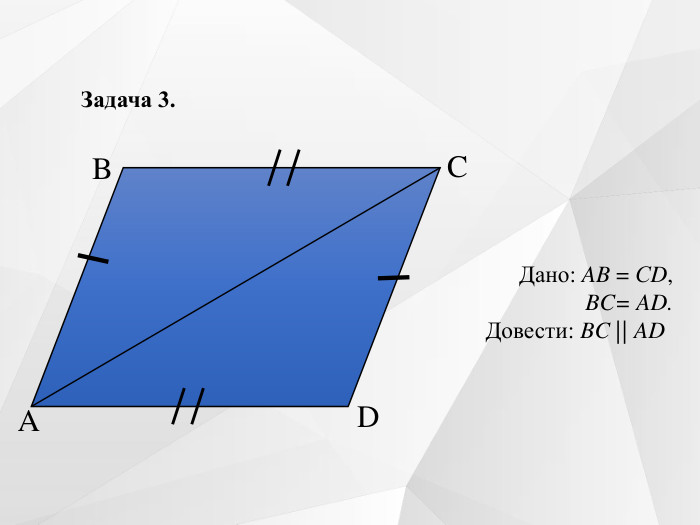
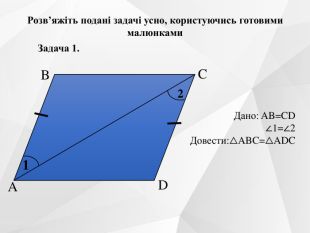
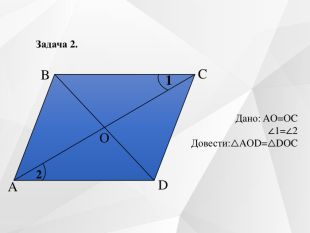
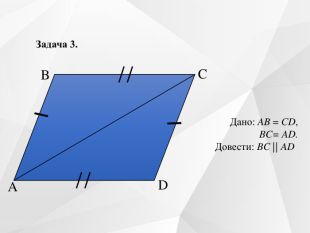
Містить усні вправи, визначення, ознаки, властивості, графічні вправи.
Перегляд файлу
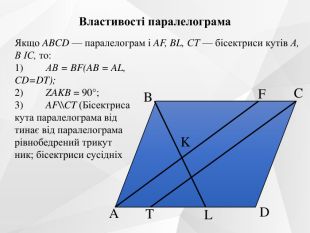
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку