Урок "Перетворення графіків функцій".
Тема. Перетворення графіків функцій.
Мета. Узагальнити й систематизувати знання студентів властивості функцій, засвоїти вміння і навички перетворювати графіки функцій у різних задачних ситуаціях; виховувати культуру володіння персональним комп’ютером, розвивати інтерес до математики й інформатики шляхом демонстрації різноманітних можливостей персонального комп’ютера.
Тип заняття: засвоєння нових знань.
Обладнання: підручники Г.П.Бевз, В.Г.Бевз Математика 10, М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук Алгебра і початки аналізу, креслярські приладдя, комп’ютери, програмний засіб GRAN.
Математика цікаві тоді,
коли дає поживу нашій винахідливості
й здатності до міркувань.
Д. Пойа
Хід заняття
І. Перевірка домашнього завдання.
Аналізуємо виконання домашніх завдань.
Один із студентів обґрунтовує відповідь до першої вправи, у другій вправі називає криву, яка є графіком функції і її властивості. Інший студент пояснює розв’язання третьої вправи.
Вправа 1. Знайдіть нулі функції.
а) у = х2+2х-8; б) ![]()
Розв’язання:
а) х2+2х-8=0;
![]()
![]()
![]()
Відповідь. -4; 2
б) ![]()
![]()
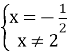
Відповідь. ![]()
Вправа 2. Побудуйте графік функції. Знайдіть її нулі. Вкажіть проміжки, на яких функція набуває додатних значень; від’ємних значень. Чи є дана функція зростаючою; спадною?
 б) у=-2х-2.
б) у=-2х-2.
Розв’язання
D(у)=(![]()
|
х |
0 |
1 |
|
у |
-2 |
-4 |
у=0, якщо х=-1;
у![]() (
(![]()
у![]()
Дана функція спадна
Вправа 3. Парною чи непарною є функція;
а) у=4х+х3; б) у=х4-1 в) у=х+1.
Розв’язання.
а) у(-4)=4(-х)+(-х)3=-4х-х3=-(4х+х3)=-у(х).
функція у=4х+х3 є непарною.
б) у(-х)=(-х)4-1=х4-1=у(х)
Функція у=х4-1 є парною.
в) у(-х)=-х+1=-(х-1)
Функція у=х+1 є ні парною, ні непарною.
ІІ. Актуалізація опорних знань студентів.
1) Назвіть властивості функцій.
2) Дайте означення області визначення й області значень функції.
3) Що таке нулі функції й проміжки знакосталості та як їх визначають, якщо функція задана за допомогою формули?
4) Дайте означення зростаючої й спадної функцій.
5) Які функції називають парними й непарними та яка властивість їх графіків?
ІІІ. Мотивація навчальної діяльності. Сприймання й усвідомлення нового матеріалу, виконання перетворень графіків функцій.
Якщо функція задана формулою у=f(х), то її графік можна побудувати за точками, склавши для цього таблицю. Але такий спосіб вимагає громіздких обчислень. На сьогоднішньому занятті ми ознайомимось з найпростішими перетвореннями графіків і навчимось будувати графіки функцій у=f(х)![]() n, де
n, де
n![]() 0, у=f(х
0, у=f(х![]() m), де m
m), де m![]() 0, у=f(х
0, у=f(х ![]() n, де m
n, де m![]() 0, n
0, n![]() 0, у=-f(х), у=аf(х), де а
0, у=-f(х), у=аf(х), де а![]() 0.
0.
Сьогодні ми працюємо в комп’ютерному класі.
На початку третього тисячоліття ні в кого не виникає сумнівів, що освічена людина повинна володіти навичками користування комп’ютером. Використання комп’ютерних технологій – не модне нововведення, а необхідність, що диктується стрімким розвитком суспільства. Саме це уможливило використання персонального комп’ютера для навчання.
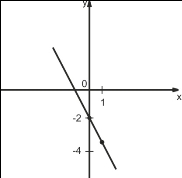
1.Побдуємо за допомогою програми GRAN1 графіки функцій у=х2, у=х2-2, у=х2+3 в одній системі координат.
Для того, щоб отримати графіки в зручному вигляді переходимо в режим «масштаб користувача», який відкривається комбінацією ALT+U. У вікні «визначення масштабу», яке появляється на екрані, вводимо мінімальне і максимальне значення х і у.
Min х=-4, Мах х=4, Міn у=-2. Мах у=12 (Введені значення підтверджується Enter чи кнопкою «Введ» у даному вікні). Після задання масштабу будуємо графіки заданих функцій. За допомогою меню «Об’єкт»/Нова функція. Формулу функції записуємо у вікні «Введіть вираз». Для того у рядку У(х) = набираємо формулу функції за допомогою кнопок вікна чи клавіатури. Далі слід задати відрізок на якому будемо виконувати побудову функції. Після чого переходимо до пункту меню «Графік»/Побудувати.
Графіки можна будувати по одному або всі одночасно, ввівши перед тим всі необхідні дані. Запис формули функції та сам графік будують відображені на екрані однаковим кольором. Дана програма дозволяє знайти координати точок, що належать графікам функцій. Для цього слід:
1) Пункт меню «Графік»/Координати (або функціональна клавіша F9 на клавіатурі)
2) Лівою кнопкою мишки клацнути по точці графіка, яка нас цікавить.
3) У верхньому лівому кутку екрана появляється координати даної точки.
 З’ясуємо, як можна одержати графік першої і другої функції із графіка функції, у=х2
З’ясуємо, як можна одержати графік першої і другої функції із графіка функції, у=х2
(мал.1)
Легко помітити, якщо змістити кожну точку графіка на 2 одиниці вниз вздовж осі у, то одержимо відповідну точку графіка функції у=х2-2.
Якщо змістити кожну точку графіка на 3 одиниці вверх вздовж осі у, то одержимо відповідну точку графіка функції у=х2+3.
Таким чином, кожну точку графіка функції у=х2-2 можна одержати із відповідної точки графіка функції за допомогою паралельного перенесення на 2 одиниці вниз вздовж осі у, а кожну точку графіка функції у=х2+3 можна одержати із відповідної точки графіка функції за допомогою паралельного перенесення на 3 одиниці вгору вздовж осі у.
(Студенти малюють зображення графіків в зошиті, користуючись шаблоном параболи).
Взагалі, графік функції у=f(х)+n, де n![]() 0 можна одержати із графіка функції за допомогою паралельного перенесення вздовж осі у на n одиниць вгору; графік функції у=f(х)-n, де n
0 можна одержати із графіка функції за допомогою паралельного перенесення вздовж осі у на n одиниць вгору; графік функції у=f(х)-n, де n![]() 0 можна одержати із графіка функції у=f(х) за допомогою паралельного перенесення вздовж осі у на n одиницю вниз.
0 можна одержати із графіка функції у=f(х) за допомогою паралельного перенесення вздовж осі у на n одиницю вниз.
Перед побудовою наступного графіка, щоб не витирати малюнок, побудовані графіки можна зберегти. Якщо дані графіки будуть використовуватися, то зберігають їх так:
1) пункт меню «Об’єкт»/ Зберегти або клавіша F2.
2) задати шлях та назву збережуваного майбутнього файлу.
Побудова всіх наступних графіків функцій буде виконуватись за наведеним вище зразком.
Витирають непотрібні графіки так:
- у вікні «Вибір», яке, знаходиться праворуч від декартової системи координат лівою кнопкою миші виділити непотрібну функцію;
- пункт меню «Об’єкт»/Вилучити або клавіша F8 на клавіатурі.
2. Графік функції у=f(х![]() m), де m
m), де m![]() 0.
0.
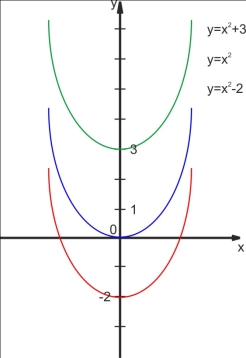
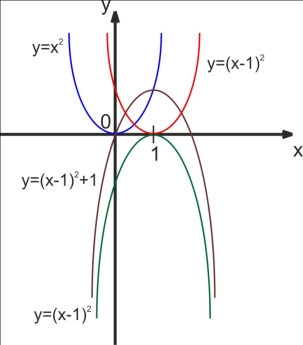
 Розглянемо функції у=(х-1)2;у=х2, у=
Розглянемо функції у=(х-1)2;у=х2, у=![]() і з’ясуємо, що собою являють їхні графіки. Для цього в одній системі координат побудуємо за допомогою програми GRAN1 графіки функцій у=(х-1)2; у=х2, у=(х+1)2 (Min х=-5, Мах х=5; Min у=-2, Мах у=14).
і з’ясуємо, що собою являють їхні графіки. Для цього в одній системі координат побудуємо за допомогою програми GRAN1 графіки функцій у=(х-1)2; у=х2, у=(х+1)2 (Min х=-5, Мах х=5; Min у=-2, Мах у=14).
(мал.2)
Що можна сказати про графіки функцій у=х2, у=(х-1)2 та у=х2, у=(х+1)2?
Графік функції у=(х-1)2 можна одержати із графіка функції у=х2 за допомогою паралельного перенесення вздовж осі х на 1 одиницю праворуч.
Графік функції у=(х+1)2 можна одержати із графіка функції у=х2 за допомогою паралельного перенесення вздовж осі х на 1 одиницю ліворуч.
Отже, графік функції у=f(х-m), де m![]() 0 можна одержати із графіка функції у=f(х) за допомогою паралельного перенесення вздовж осі х на m одиниць праворуч; графік функції у =f(х+m), де m
0 можна одержати із графіка функції у=f(х) за допомогою паралельного перенесення вздовж осі х на m одиниць праворуч; графік функції у =f(х+m), де m![]() 0 можна одержати із графіка функції у=f(х) за допомогою паралельного перенесення вздовж осі х на m одиниць ліворуч.
0 можна одержати із графіка функції у=f(х) за допомогою паралельного перенесення вздовж осі х на m одиниць ліворуч.
(Студенти виконують малюнки в зошиті)
3. Графік функції у=f(х![]() m)
m)![]() n, де m
n, де m![]() 0, n
0, n![]() 0.
0.
Розглянемо функцію у=(х-2)2+1. Виконуємо побудову за допомогою програми GRAN1.
Її графік можна одержати, якщо графік функції у=х2паралельно перенести вздовж осі х на 2 одиниці праворуч, а потім вздовж осі у на 1 одиницю вгору.
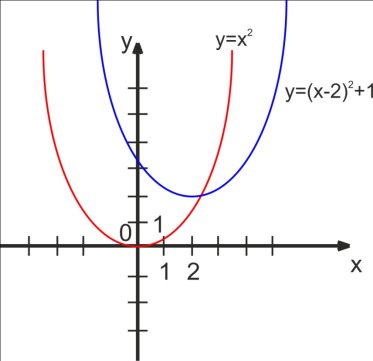
(мал.3)
Графік функції у=f(х-m)+n можна одержати із графіка функції у=f(х) за допомогою двох паралельних перенесень: параллельного перенесення вздовж осі х на m одиниць вправо, якщо m![]() 0, або на –m одиниць вздовж осі х вліво, якщо m
0, або на –m одиниць вздовж осі х вліво, якщо m![]() 0, та паралельного перенесення вздовж осі у на n одиниць вгору, якщо n
0, та паралельного перенесення вздовж осі у на n одиниць вгору, якщо n![]() 0, або на –n одиниць вниз, якщо n
0, або на –n одиниць вниз, якщо n![]() 0.
0.
(Студенти малюють зображення графіка в зошиті за допомогою шаблона параболи у=х2).
4. Графік функції у=-f(х)
Побудуємо за допомогою програми GRAN1 графік функції у=-х2. Порівнюємо графіки функції у=-х2 і у=х2 (Мin х=-5, Мах х=5; Min у=-14, Maх у=14).
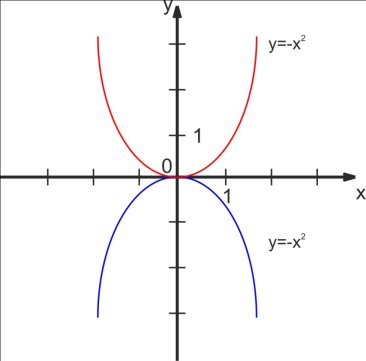
(мал.4)
При одному і тому самому значенні ї значення цих функцій симетричні відносно осі х.
Отже, графік функції у=-х2 можна одержати в результаті відображення графіка функції у=х2 симетричної осі х. (Побудову виконують в зошиті за допомогою шаблону у=х2)
Графік функції у=-f(х) можна одержати із графіка функції у=f(х) за допомогою симетрії відносно осі х.
5. Графік функції у= а![]() f(х), де а
f(х), де а![]() 0
0
Побудуємо за допомогою комп’ютера графік функції у=2х2 (мал.5) В тій же системі координат побудуємо графік функції у=х2
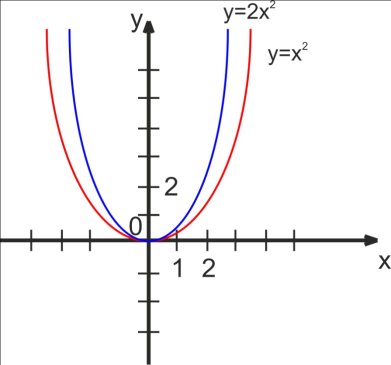
(мал.5)
Порівняємо графіки функцій у=2х2 і у =х2.
Ми бачимо, що при одному і тому самому значення х значення функції 2х2 у два рази більше значення функції у=х2. Це означає, що кожну точку графіка у=2х2 можна одержати із точки графіка функції у=х2 з тією ж абсцисою збільшенням її ординати в 2 рази.
Кажуть, що графік функції у=2х2 одержимо в результаті розтягування графіка функції у=х2 від осі х вздовж осі у в 2 рази.
Побудуємо за допомогою програми GRAN1 в одній системі координат графіка функцій у=![]()
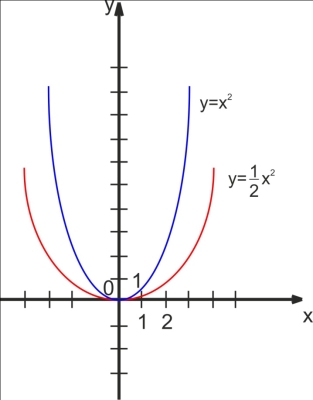
(мал.6)
Порівнюємо отримані графіки.
Кожну точку графіка функції у=![]() 2 можна одержати із точки графіка у=х2 з тією ж абсцисою зменшенням її ординати в 2 рази. Кажуть, що графік функції у=
2 можна одержати із точки графіка у=х2 з тією ж абсцисою зменшенням її ординати в 2 рази. Кажуть, що графік функції у=![]() х2 одержано в результаті стиснення графіка функції у=х2 до осі х вздовж осі у в 2 рази.
х2 одержано в результаті стиснення графіка функції у=х2 до осі х вздовж осі у в 2 рази.
Отже, графік функції у=а![]() f(х), де а
f(х), де а![]() 0 можна одержати із графіка функції у=f(х) розтягнувши останній від осі х в а разів, якщо а
0 можна одержати із графіка функції у=f(х) розтягнувши останній від осі х в а разів, якщо а![]() 1, стиснувши його до осі х в
1, стиснувши його до осі х в ![]() разів, якщо 0
разів, якщо 0![]() а
а![]() 1.
1.
ІV. Осмислення вивченого матеріалу.
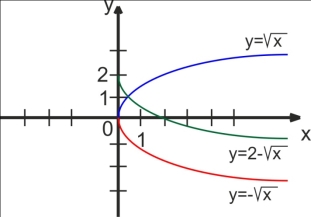
Побудувати за допомогою шаблону параболи у=х2 графіки функцій:
а) у=2![]() ; б) у=(х-1)2 +1 (правильність побудови студенти перевіряють за допомогою комп’ютера).
; б) у=(х-1)2 +1 (правильність побудови студенти перевіряють за допомогою комп’ютера).
Розв’язання.
а) Будуємо графік функції у=![]() . За допомогою симетрії відносно осі х одержуємо графік функції у=-
. За допомогою симетрії відносно осі х одержуємо графік функції у=-![]() . Паралельно переносимо його уздовж осі у на дві одиниці вгору. Одержуємо шуканий графік.
. Паралельно переносимо його уздовж осі у на дві одиниці вгору. Одержуємо шуканий графік.
б) Послідовно будуємо графіки таких функцій:
1) у=х2 2) у=(х-1)2; 3) у=-(х-1)2 4)у=-(х-1)2+1
V. Домашнє завдання.
Виготовити шаблони парабол у=2х2; у=3х2; у=![]() х2; у=
х2; у=![]() х2 .
х2 .
За підручником [1] §4 Вправа 1. Побудуйте графік функції у=х2+5.
Вправа 2. Побудуйте графік функції у=(х-2)2-4.
Користуючись графіком знайдіть:
а) область значень функції;
б) усі значення х, при яких функція набуває додатних значень;
в) проміжок на якому функція зростає.
VІ. Підсумок заняття.
Що нового ви дізналися і чого навчилися на сьогоднішньому занятті?
Це заняття є яскравим свідченням того, використання комп’ютера робить математику – всеосяжною наукою.


про публікацію авторської розробки
Додати розробку
