Урок "Перетворення графіків функцій. Самостійна робота".

Тема. Перетворення графіків функцій. Самостійна робота.

Мета: узагальнити навички перетворення графіків функцій; розвивати графічну культуру студентів, формувати навички самостійної  роботи; виховувати зосередженість, охайність.

Тип заняття. Формування навичок і вмінь.

     Обладнання: підручники Г.П.Бевз, В.Г.Бевз Математика 10, М.І.Шкіль, З.І.Слєпкань, О.С.Дубинчук Алгебра і початки аналізу, креслярські  приладдя, шаблони парабол y=x²; у=2х²;  у=3х²; у=х² ; у=х²; комп'ютери, програмний засіб GRAN₁

Так  звана   самостійна робота - це  вершки

математики... Без роботи такого характеру вивчення

математики -  майже даремна річ ...

                         Дж. В. Янг

Хід заняття

І. Перевірка домашнього завдання.

Сьогодні ми знову працюємо в комп'ютерному класі. Ви вже вмієте користуватися програмою GRAN₁. То ж давайте перевіримо домашнє завдання, користуючись нею

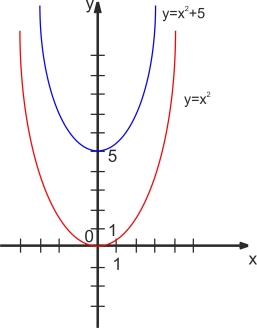
1. Побудуйте графік функції у=х²+5.

Розв’язання.

Будуємо графік функції у=х² Паралельно переносимо його вздовж осі  у на 5 одиниць вгору. Одержуємо шуканий графік.

 

 

 

 

 

 

2. Побудуйте графік функції y=(x-2)²-4. Користуючись графіком, знайдіть:

а) область значень функції:

б) усі значення х, при яких функція набуває додатних значень;

в) проміжок, на якому функція зростає.

Розв’язання 

Послідовно будуємо графіки таких функцій: 1) у=х²; 2) у=(х-2)²;

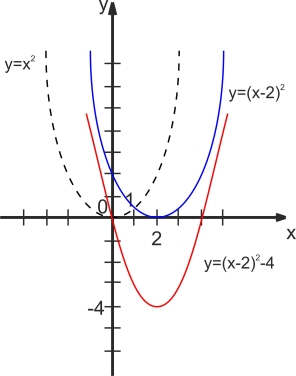3) у=(х-2)² -4.

 

 

 

 

 

 

 

 

 

 

 

 

а) Е(у)=[-4;)

б) у>0 при х є (-;0) U (4;)

в) зростає на [2;).

II. Актуалізація опорних знань студентів.

Усне виконання вправ.

1) Визначити напрямок віток параболи.

у=3х²; у=-4х²; у=х²; у= - х²

2) Як користуючись графіком функції у=х², побудувати графік функції:

а) у= -х²;  б) у=2х²;   в) у=х²;   г) у=х²+2;  д) у=х²-4;  е) у=(х-4)²;

є) у=(х+5)²;      ж) у=(х-3)²+1.

Відповідь: а) симетрією відносно осі х;

б) розтягнувши від осі х в 2 рази;

в) стиснувши до осі х в   рази;

г) перенесенням уздовж осі у на 2 одиниці вгору;

д) перенесенням уздовж осі у на 4 одиниці вниз;

е) перенесенням уздовж осі х на 4 одиниці праворуч;

є) перенесенням уздовж осі х на 5 одиниць ліворуч;

ж) перенесенням уздовж осі х на З одиниці праворуч і вздовж                осі у на 1 одиницю вгору.

III. Формування умінь і навичок.

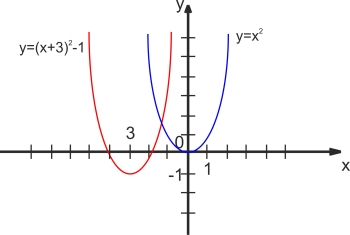
1. Побудуйте графік функції у= (х-3)²-1. Користуючись графіком      знайдіть:

а) область значень функції;

б) усі значення х, при яких функція набуває від'ємних значень;

в) проміжок на якому функція спадає.

Колективно  розглядаємо  перетворення  графіка  за допомогою програми GRAN₁. Тоді студенти, користуючись шаблоном параболи у=х² виконують малюнок в зошиті. Студенти  по черзі коментують виконання завдань вправи.

Розв 'язання.

Щоб побудувати графік функції у=(х+3)²-1  будуємо спочатку графік функції у=х². Тоді паралельно переносимо його вздовж осі х на 3 одиниці ліворуч, а потім  уздовж осі у на 1 одиницю вниз.

 

 

 

 

 

 

 

 

 

 

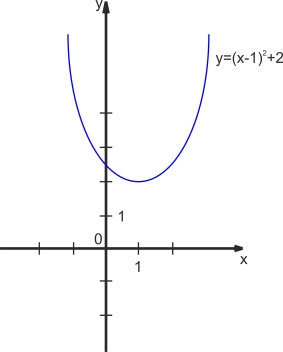
2. Побудувати, використовуючи шаблон  параболи графік функції

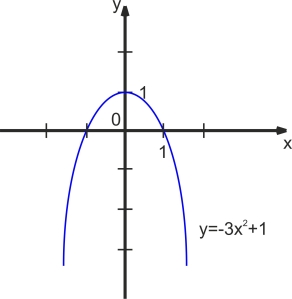
а) у=(х-1)²+2; б) у=-3х²+1.

Студенти виконують самостійно в зошитах. Правильність перевіряють за допомогою програмного забезпечення.

Розв'язання.

а) Користуючись шаблоном у=х² будуємо спочатку графік функції у=х².

Тоді паралельно переносимо його вздовж осі х на 1 одиницю вправо,  а потім уздовж осі у на дві одиниці вгору.

 

 

 

 

 

 

 

 

 

 

 

 

б)  Користуючись  шаблоном  у=3х² будуємо  графік  функції у=3х² .

Відображаємо йоге симетрично  відносно осі  х і  паралельно  переносимо уздовж осі у на І одиницю вгору. Одержуємо графік функції у=-3х²+1.

 

 

 

 

 

 

 

 

 

 

3. Уміння будувати графіки функцій і рівнянь часто допомагає розв'язувати різні задачі.

Побудуйте в одній системі координат графіки функцій у= та у=-х²+2,5.  Скільки коренів мас рівняння.

Перед розв'язуванням доцільно повторити із студентами, що називається розв'язком рівняння, в чому полягає графічний спосіб розв'язування рівнянь.

Розв'язання.

1) Будуємо графік функції у= . Паралельно переносимо його вздовж осі х на 1 одиницю ліворуч. Одержуємо графік у.

2) Будуємо графік функції у=х². Відображаємо його симетрично відносно х і паралельно переносимо уздовж осі  у на 2,5 одиниці вгору. Одержуємо графік функції у= -х²+2,5.

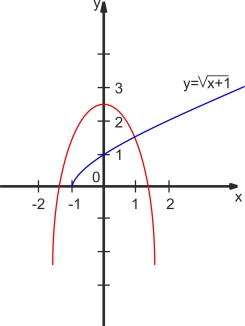3) Абсциса точки перетину графіків функцій буде розв'язком рівняння.

 

 

 

 

 

 

 

 

 

 

Отже, х=1.

Відповідь. 1

IV. Закріплення умінь і навичок.

    Самостійна робота.

Варіант 1.

1. Використовуючи шаблон  параболи  у=х² побудуйте в одній системі координат графіки функцій: у=-: у=--1; у=-(х-1)²;

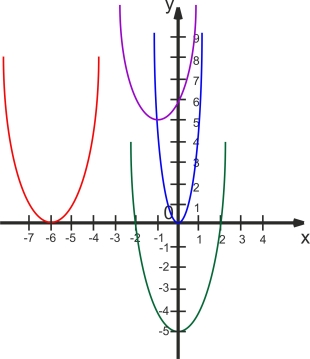
2.Записати функції, графіки яких зображені на екрані монітора:

 

 

 

 

 

 

 

 

 

 

Варіант 2

1. Використовуючи шаблон параболи у= х², побудуйте в одній системі координат графіки функцій: у=х²+3; у=(х+3)²; у=-(х+3)²;

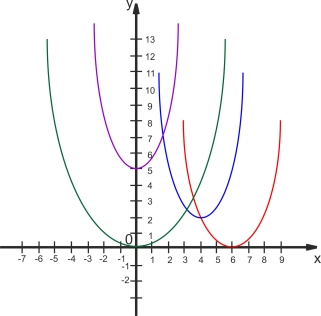
2. Записати функції, графіки яких зображені на екрані монітора:

 

 

 

 

 

 

 

 

 

 

 

 

Розв’язання.

Варіант 1.

 

 

 

 

 

 

 

 

 

 

 

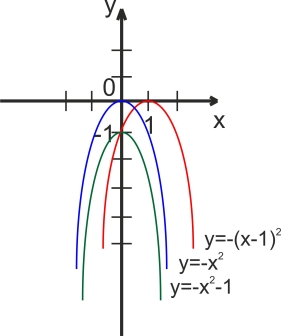
2)  а) у=х²+5;

б) у=х²;

в) у=(х-6)²;

г) у=(х-4)²+2.

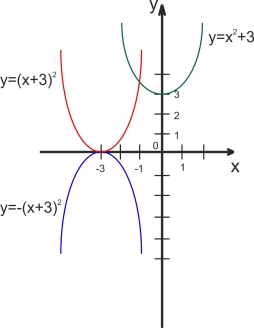Варіант 2.

1.

 

 

 

 

 

 

 

 

 

 

2.  1)у=х²-5

  2) у=4х²;

3) у=(х+6)²;

4) у=(х+1)²+5.

V. Підсумок заняття.

На занятті ви будували графіки функцій за допомогою лінійних перетворень, продемонстрували навички самостійного  мислення,  показали вміння  користуватися  комп'ютером;   культуру   математичного  мовлення.

VI. Домашнє завдання.

За підручником [1] Розділ 1 § 4,5.

1. Побудуйте графік функції: а) у=х+2; б) у=(х-1)²;  в) у= -(х+1)²+5