Урок "Контрольна робота "Функція. Перетворення графіків функцій."

Тема: Функція. Перетворення графіків функцій.

Контрольна робота.

Мета: перевірити навчальні досягнення студентів з теми; формувати 

           самостійність.

       Обладнання: роздатковий матеріал, креслярські  приладдя.

Тип заняття: контрольно-заліковий.

Перша умова, якої треба дотримуватись

у математиці – це бути точним, друга – бути

ясним і, наскільки можливо, простим.

Л.Карно

Хід заняття

Контрольна робота оцінюється 12 балами, у ній 6 завдань, кожне з яких оцінюється 2 балами.

 Варіант 1       Варіант 2

1. Функцію задано формулою:

       

а) знайдіть f(1)

б) Визначте, за яких значень х виконується рівність

f(х)=-1 

в) Знайдіть область визначення і нулі функції.

2.Визначте парність функції:

а) у=5-х²;       а) у=5+х⁴;

б) у=х²+х³;       б) у=х³-х²;

в) у=2;        в) у=1.

3.Використовуючи шаблон параболи у=х²,

Побудуйте в одній системі координат графіки функцій.

у=-х²;        у=х²-3;

у=-х²+1;       у=(х-3)²;

у=-(х+1)²;       у=-(х-3)^2.

4. Скоротіть дріб

                                                        

 

5. Визначте значення х, за яких функція

у=-х²+2х-1;      у=-х²-6х-9

набуває найбільшого значення. Знайдіть це значення.

6. Побудуйте графік функцій

                   

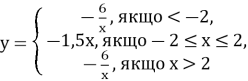
Розв’язання задач

Варіант 1.

1. а) =

б)

                             

При х=2 f(х)=-1

в) х+1

D(f)=()U(-1;)

                             

Нулі функції (5;0)

Відповідь: а) -2

         б) при х=2;

                   в) D(f)=()U(-1;)

         (5;0)

 2. а) у(-х)=5-(-х)²=5-х²=у(х), виконується умова парності функції

у=5-х² – парна

б) у(-х)=(-х)²+(-х)³=х²-х³=-(х³-х²) – не виконується умова ні парності, ні непарності функції

у=х²+х³ ні парна, ні непарна

в) у(-х)=2=у(х) виконується умова парності функції

Відповідь: а) парна;

         б) ні парна, ні непарна;

         в) парна.

3.

 

 

 

 

 

 

 

 

 

4. Розкладемо  на множники чисельник дробу

9х²-6х+1=(3х-1)²

Розкладемо на множники знаменник дробу

6х²+х-1=0

D=1+24=25

6х²+х-1=6(х+

Тоді

 

Відповідь:

5. –х²+2х-1=-(х²-2х+1)=-(х-1)²

Вираз (х-1)² при будь-яких значеннях х невід’ємний, але –(х-1)² не додатний. Тому дана функція набуває найбільшого значення 0 при х=1.

Відповідь: y_найб.=0 при х=1.

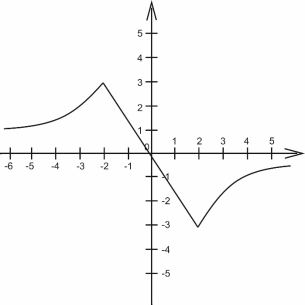
6. графік функції складається з двох частин гіперболи у=  

для х   і частини прямої  у=1,5х для -2

 

 

 

 

 

 

 

 

 

 

 

Варіант 2

1. а) f(1)=

б)

                             

При х=-2,5 f(х)=-1.

в) х-3

D(f)=(-

                             

Нулі функції (-8;0)

Відповідь:     а) -3;

   б) при х=-2,5;

   в) D(f)=(-

 (-8;0)

2. а) у(-х)=5+(-4)²=5+х⁴=у(х), виконується умова парності функції

у=5+х⁴ – парна

б) у(-х)=(-х)³-(-х)²=-х³-х²=-(х³+х²) – не виконується умова ні парності, ні непарності функції

у=х³-х² ні парна, ні непарна

в) у(-х)=1=у(х) виконується умова парності функції

Відповідь:  а) парна;

 б) ні парна, ні непарна;

 в) парна.

 

 

 

 

 

 

 

 

 

 

 

4. Розкладемо на множники чисельник дробу

8х²-2х+1=0

D=4+32=36

8х²-2х-1=8(х+=(4х+1)(2х-1)

Розкладемо на множники знаменник дробу

16х²+8х+1=(4х+1)²

Тоді

Відповідь:

5. –х²-6х-9=-(х²+6х+9)=-(х+3)²

Вираз (х+3)² при будь-яких значеннях х невід’ємний, але –(х+3)²не додатний. Тому дана функція набуває найбільшого значення 0 при х=-3.

Відповідь: у_найб.=0 при х=-3

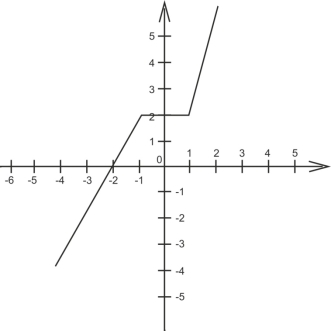
6. Графік функції складається з частини прямих у=2х+4 для х