Лекція «Перетворення многочлена на квадрат суми або різниці двох виразів»

Найдосконаліший мозок іржавіє без дії

Шерлок Холмс

 

Юний друже!

 З лекції  «Перетворення многочлена на квадрат суми або різниці двох виразів» ти дізнаєшся про ще один спосіб розкладання многочлена на множники і навчишся самостійно його використовувати.

Будь уважним/уважною!

 Після засвоєння змісту теми ти:

• матимеш уявлення про альтернативний спосіб застосовувати формули скороченого множення, які вивчив минулого уроку, навчишся використовувати їх при розв’язанні конкретних математичних задач;
• дослідиш доведення і застосування формул для нестандартних ситуацій;
• зможеш розв’язувати якісні завдання на розкладання многочлена на множники;

• розвинеш логічне мислення, впевненість у власних силах, наполеглевість;
• навчишся використовувати формули скороченого множення, застосовувати свої знання і вміння для розв’язування прикладних математичних задач у повсякденному житті.

 

План лекції

1. Розкладання многочленів на множники з використанням формул квадрата двочлена
2. Застосування формул скороченого множення
3. Для тих, хто бажає дізнатися про ВСЕ

 

1. Розкладання многочленів на множники з використанням формул квадрата двочлена.

Юний друже, в повсякденному житті часто виникають ситуації в яких ти маєш відстоювати свою позицію або доводити свою думку. У навчанні та сама ситуація.

Доведи, що многочлен х²+4 - 4х не може набувати від’ємних значень.

Спробуй дослідити, чи пов’язаний цей многочлен з формулами скороченого множення, які ти вже знаєш.

х²+4 - 4х

Дійсно, перші два одночлени є квадратами х² і 2², а третій є подвійним множником 2·2·х. Зауважемо, сума многочленів може записуватися у будь-якому порядку. Наявність знака “мінус” пояснюємо як наявність доданка з від’ємним коефіціентом.

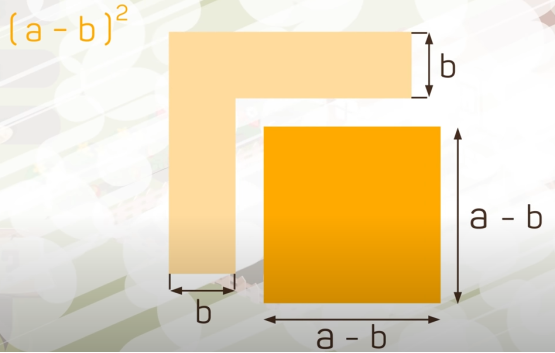
Перепишемо формули квадрата різниці та квадрата суми двох виразів, помінявши місцями їх ліві і прави частини:

a2-2ab+b2=(a-b)2 a2+2ab+b2=(a+b)2

Таке перетворення називають “згортанням” тричлена у квадрат двочлена або у повний квадрат.

Тричлен, який можна подати у вигляді квадрата двочлена називають повним квадратом.

Отже,  х²+4 - 4х= х² - 4х+4= х² - 4х+2²=(х-2)²

Отримали квадрат двочлена, який може бути лише додатним або нулем. Що і треба було довести.

Таким чином маємо можливість за допомогою зазначених вище формул перетворити тричлен на квадрат двочлена. Оскільки квадрат двочлена можна подати у вигляді добутку (а-b)²=(а-b)·(а-b), можна стверджувати, що таке перетворення є одним із способів розкладання многочлена на множники.

 

2. Застосування формул скороченого множення

Саме розкладання на множники дає можливість розв’язати деякі конкретні математичні задачі.

Розглянемо декілька прикладів.

Приклад 1. Подай тричлен у вигляді квадрата двочлена:

1) 9х²+24ху+16у²;

2) 25а⁴-20а²b³+4b⁶.

Зауваження! Перш за все, подай два одночлена у вигляді квадрату. Пам’ятай, що доданки можуть бути записані у будь-якому порядку. Зверни увагу на подвійний добуток.

Розв’язання:

9х²+24ху+16у²=(3х)²+2·3х·4у+(4у)²=(3х+4у)²

25а⁴-20а²b³+4b⁶=(5а²)²-2·5а²·2b³+(2b³)²=(5а²-2b³)²

Приклад 2. Розв’яжи рівняння х²+10х=-25.

Зауваження! Перенеси число з правої частини рівняння у ліву, яку тепер можна перетворити на квадрат двочлена.

Розв’язання:

х²+10х=-25;

х²+10х+25=0;

х²+2·х·5+5²=0;

(х+5)²=0.

Оскільки значення квадрата дорівнює нулю лише тоді, коли його основа дорівнює нулю, то:

Х+5=0;

Х=-5.

Відповідь: -5.

Приклад 3.

Перетвори многочлен на квадрат різниці 9х²-6ху+у².

Розв’язання:

9х²-6ху+у²=(3х)²-2·3х·у+у²=(3х-у)².

Зауваження! Оскільки від’ємний коефіцієнт тільки у подвійного добутка і доданки можуть надаватися у будь-якому порядку, то двучлен в квадраті можна записати так: (у-3х)². Перевіримо:

(у-3х)²=у²-2·3х·у+(3х)²=(3х)²-2·3х·у+у²=(3х-у)²;

(у-3х)²=(3х-у)².

Отже, відповідь (у-3х)² також буде правильною.

Приклад 4. Якого найменшого значення набуває вираз 4х²-12х-7?

Зауваження! Спробуємо виділити з поданого тричлена квадрат двочлена. Подамо перший одночлен у вигляді квадрата одночлена 4х²=(2х)². Другий одночлен розглянемо як подвійний добуток 12х=2·2х·3.

Зверни увагу! Щоб “згорнути” тричлен у квадрат двочлена подвійний добуток “диктує”, яким має бути третій одночлен. Це 3².

Тобто вираз має бути 4х²-12х+9, а не 4х²-12х-7.

В таких випадках ми маємо додати потрібний нам вираз і відразу його відняти. Результат не зміниться!

Розв’язання:

4х²-12х-7=4х²-12х+9-9-7=(4х²-12х+9)-9-7=((2х)²-2·2х·3+3²)-16=(2х-3)²-16

Проаналізуй, яким найменшим може бути результат?

Так, дійсно, квадрат будь-якого виразу набуває найменшого значення нуль. Тоді 0 -16=-16.

Відповідь: Даний вираз набуває найменшого значення -16.

 

3. Для тих, хто бажає дізнатися про ВСЕ

Скарбничка ідей

Іноді складні обчислення зводяться до простих, якщо вдало використовувати потрібну формулу скороченого множення.

Розглянемо приклади.

Обчисли значення виразу 4,2²+4,2·10,6+5,3².

Не дарма формули скороченого множення мають таку назву. Шукаємо формулу, щоб скоротити розв’язання. Отже:

4,7²+4,7·10,6+5,3²=4,7²+2·4,7·5,3+5,3²=(4,7+5,3)²=10²=100

Відповідь: 100.

“А що, так можна було?”

Можна дуже швидко без допомоги лічильних пристроїв підносити до квадрату числа, які закінчуються на 5.

Обчислити можна за таким алгоритмом:

                Відкинути останню цифру 5

                Отримане число помножити на наступне

                Наприкінці дописати 25

Дійсно 25²=625 (2·3=6);

85²=7225  (8·9=72);

105²=11025  (10·11=110);

Чому так відбувається? Чаклунство? Ні, формула скороченого множення. Давайте розбиратися!

Доведення.

Будь-яке натуральне число, яке закінчується на 5 можна записати у вигляді х·10+5.

При чому х — будь-яке натуральне число. Тоді (х·10+5) — будь-яке натуральне число, яке закінчується на цифру 5.

Як от 25=2·10+5, або 85=8·10+5 і так далі.

Піднесемо це число до квадрату за допомогою формули скороченого множення, тобто:

(10х+5)²=100х²+2·10х·5+25=100х²+100х+25.

Далі виносимо за дужки спільний множник перших двох одночленів.

100х²+100х+25=100х(х+1)+25.

Або так: х·(х+1)·100+25.

Звичайно х+1, це наступне число після х. Ось ми і отримали початковий алгоритм.

Шукай і пробуй пізнати цей світ! Ти зможеш!