Урок "Перпендикулярність прямої та площини. Повторення"

Тема. Перпендикулярність прямої та площини.

Мета:  повторити і закріпити знання учнів з теми  «Перпендикулярність прямих і площин у просторі»; перевірити вміння учнів застосовувати набуті знання до розв’язування вправ і задач; розвивати  логічне мислення, творчі здібності, просторову уяву учнів, культуру спілкування, вміння формулювати відповіді на запитання та аналізувати відповіді своїх товаришів; виховувати наполегливість,   відповідальність за свої знання, інтерес до геометрії як науки.

 

Хід уроку

І. Актуалізація опорних знань

Хай живе теорія – без теорії немає практики.

1. Що вивчається в стереометрії?
2. Назвіть аксіоми стереометрії.
3. Скільки випадків перпендикулярності і які розглядають у стереометрії?
4. Дві  прямі називають перпендикулярними, якщо кут між ними дорівнює….
5. Означення прямої, перпендикулярної до площини
6. Ознака перпендикулярності прямої і площини
7. Властивість перпендикулярних прямої і площини
8. Означення перпендикуляра, проведеного з даної точки до даної площини.
9. Властивість перпендикуляра і похилої
10.          Теорема про три перпендикуляри

Тестування

1.  У просторі дано пряму а і точку А поза нею, скільки існує прямих, що є перпендикулярними до прямої а і проходять через точку А?

а) визначити неможливо;

б) одна;

в) нескінченна множина;

г) жодної.

2. Скільки площин, перпендикулярних до даної прямої можна провести через точку, що лежить на даній прямій?

          а) нескінченну множину;

б) тільки одну;

в) тільки дві;

г) жодної.

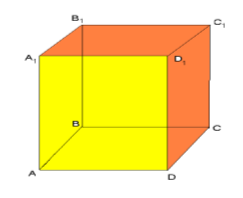
3. Використовуючи малюнок, вкажіть пряму, що перпендикулярна до прямої СС₁ і проходить через точку А.

а) СВ   б) АС   в) CD   г) А₁С₁

4. Вкажіть пряму, яка перпендикулярна до площини АВВ₁

а) BD   б) ВС   в) АВ   г) АС

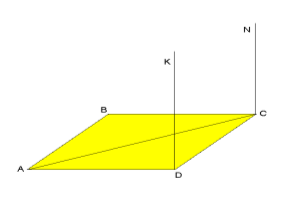
5. Яким є взаємне розміщення прямих KD i  NC, якщо АК _┴ (АВС) і NC _┴ (АВС)?

а) паралельні;

б) мимобіжні;

в) перпендикулярні;

г) перетинаються.

6. Яким є взаємне розміщення прямої  KD  і площини АВС, якщо KD ║NC i NC _┴ (ABC)?

а) паралельні;

б) визначити неможливо;

в) не перетинаються;

г) перпендикулярні

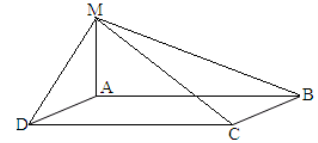
7. Відрізок АМ проведено перпендикулярно до площини   прямокутника   АВСD. Який відрізок має більшу довжину?

    а) МА;        б) МD;     в) МВ;      г) МС;        д) АD.

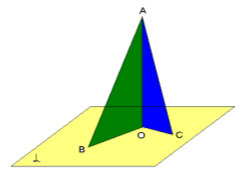
8. З точки А до площини проведено дві похилі АВ і АС і перпендикуляр АО. Відомо, що АВ >АС. Виберіть правильне твердження.

а) АВ < AO   б) CO > OB  

в) AC < AO   г) CO < OB

 

Задачі за готовими малюнками.

 

 

 

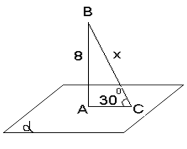
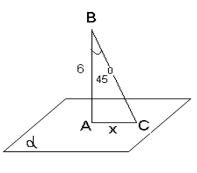
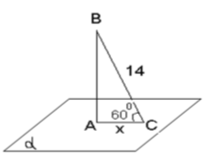
IІ. Узагальнення і систематизація набутих знань та вмінь.

Від теорії до практики

1. Через вершину гострого кута прямокутного трикутника АВС з прямим кутом С проведено пряму АD, перпендикулярну до площини трикутника. Знайдіть відстань від точки D до вершин В і С, якщо АС = а, ВС = b,       АD = с.

 

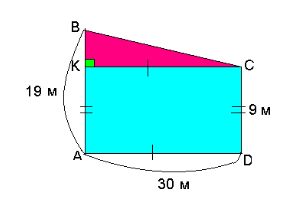
2. Потрібно протягнути два електричні дроти від стовпа до будинку. На стовпі вони кріпляться на висоті 19 м, а на стіні будинку - 9 м. Скільки потрібно дроту, якщо відстань від стовпа до будинку становить 30 м, а на кріплення і провисання слід додати 5% знайденої довжини.

Розв'язання

Стовп перпендикулярний площині Землі і стіна будинку перпендикулярна площині Землі, отже, оскільки дві прямі, перпендикулярні одній і тій самій площині, паралельні між собою, з цього випливає, що математична модель задачі - прямокутна трапеція.

Отже, АВ = 19 м, CD = 9 м, AD = 30 м. Знайдемо ВС.

Опустимо перпендикуляр СК на сторону АВ.  АК = CD = 9 м, отже,

ВК = АВ - АК = 19 - 9 = 10 (м). К С = AD = 30 м.

З Δ ВСК ():

ВС =   = = (м)

1) 10∙2 = 20 (м) - довжина 2-х дротів.

2) 20∙0,05 = (м) - на провисання.

3) 20 = 21 (м)

Відповідь: необхідно 21 м дроту.

 

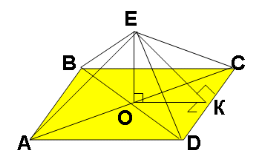
3. Чотирисхилий дах будинку квадратної форми зі стороною 16м має висоту 6м. Скільки квадратних метрів дахового заліза піде на покриття, якщо витрати на згин і обрізки становлять 6%?

                                              Розв’язання

Нехай дано  квадрат АВСD , АВ = 16м. EO _┴ (ABCD) , EO=6м. Оскільки т. Е рівновіддалена від сторін АВСD, то т. О – центр вписаного кола ( точка

перетину діагоналей). Якщо ЕК _┴ СD, то за оберненою теоремою про три перпендикуляри ОК _┴ СD, ОК=8 м.

З ∆ EOК, <O = 90⁰, за теоремою Піфагора EK² = EO² + ОК². .   

S= 4S_∆CDE, S_∆CDE = CD·ЕK =·16 · 10 = 80(м²). S = 4 · 80 = 320(м²).

S₁ = 320 + 0,06 · 320 = 339,2 (м²).

Відповідь: 340 м².

 

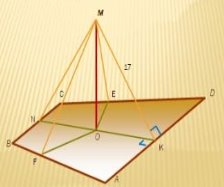
4. Якої висоти повинен бути ліхтарний стовп на присадибній ділянці, що має форму рівнобедреної трапеції з основами 16м і 30м, якщо відстань від ліхтаря до кожної із сторін ділянки 17м.

    

 

                                              Розв’язання.

Нехай дано трапецію ABCD, ( AD ║ BC) ,  AB = CD, AD = 30м , BC = 16м. MO _┴(ABCD). Оскільки т. М рівновіддалена від сторін трапеції, то основа перпендикуляра т. О – центр вписаного кола.

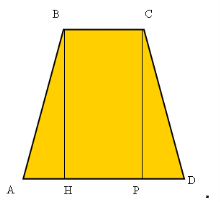
Виконаємо планіметричний малюнок. Проведемо СР _┴ AD, ВН _┴ AD. ВСРН – прямокутник . НР = ВС = 16м.

Так як АВСD – рівнобічна трапеція, то PD = AH = (30 - 16) : 2 = 7(м). Оскільки в трапецію можна вписати коло, то АВ + СD = ВС + АD.

АВ = СD =(30 + 16) : 2 = 23(м). З ∆ DCP ,<P = 90⁰ , за теоремою Піфагора СР² = СD² -  PD², . OE= .

З ∆ МОЕ, <О = 90⁰ , за теоремою Піфагора MO² =  ME² - OE², .

Відповідь:13 метрів.

 

ІІІ. Домашнє завдання: с. 219, № 1053, 1089