Урок "Первісна та інтеграл"
План уроку
Предмет: Алгебра і початки аналізу
Тема: Первісна та інтеграл
Тема уроку: Розв’язування задач по темі
Тип уроку: Урок узагальнення і систематизації
Вид уроку: Урок-гра: «Математичний калейдоскоп»
Мета уроку:
✓загальноосвітня: систематизувати знання з теми: «Первісна та інтеграл», закріпити навички та вміння застосовувати знання з теми до розв’язування вправ;
✓розвиваюча: розвивати пізнавальний інтерес, навички колективної роботи; використовувати знання, вміння і навички в нових ситуаціях; формувати навички контролю і самоконтролю;
✓ виховна: виховувати працьовитість, вміння об’єктивно оцінювати результати своєї і колективної праці; прищеплювати бажання мати якісні, глибокі знання, доводити справу до кінця.
Обладнання: роздатковий матеріал, інтерактивна дошка
Форма роботи: робота в двох малих групах
Час роботи: 45 хвилин
Форма оцінювання: загальна оцінка на групу, можливе збільшення оцінки на один бал найактивнішим гравцям
Хід уроку
Предмет математики такий серйозний, що корисно не нехтувати нагодою робити його трохи цікавішим
Блец Паскаль
І. Організаційний момент
Група поділяється на 2 команди, обирається капітан (до початку занять). Команди займають місця за своїми «круглими столами».
У нас сьогодні будуть змагатися команди «Розумашки» та «Чарівні інтегральчики».
На столі перед усіма членами команди лежать «Аркуші самоконтролю» (додаток 1), де кожен ставить знак «+» за надану ним вірну відповідь.
У рядку навпроти прізвища сумуються знаки «+», і ви зможете самостійно виставити собі оцінку за роботу наприкінці уроку.
А також перед вами стоїть ялинка, прикрашена різноманітними солодощами:
▪ шоколадна цукерка відповідає повній відповіді (4 бали);
▪карамелька – неповній відповіді (3 бали); ▪бублик – доповненню (2 бали).
Експерти за кожну відповідь зрізають для команди відповідні солодощі.
ІІ. Узагальнення і систематизація знань
Гра складається з шести геймів.
I гейм «Далі-далі»
Цей гейм найазартніший, оскільки в ньому кожна команда протягом однієї хвилини відповідає на запитання і може заробити свої переможні бали.
Для точного відліку часу будемо користуватися пісочним годинником.
Якщо команда не знає відповіді, то дає сигнал словом «далі».
Починає команда «Розумашки».
РОЗУМАШКИ ЧАРІВНІ ІНТЕГРАЛИ
|
1. Функція F(x) називається первісною для f(x) на деякому проміжку, якщо… |
1. Скільки первісних має функція? |
|
2. Чим відрізняються первісні для однієї і тієї самої функції? |
2. Інтеграл суми функцій дорівнює… |
|
3. Яка фізична задача приводить до поняття інтегралу? |
3. Геометричний зміст основної властивості первісної. |
|
4. Назвіть формулу Ньютона-Лейбніца. |
4. Один з великих вчених, що вніс лепту у обчислення інтегралів, якому впало на голову яблуко. |
|
5. Операція, обернена до диференціювання, називається… |
5. Невизначеним інтегралом називається… |
|
6. Як змінюється запис формули інтегралу при перестановці меж інтегрування? |
6. Криволінійною трапецією називається фігура… |
|
7. Назвіть відомі вам застосування інтеграла. |
a 7. f (x)dx, якщо f (x) 0 для всіх x[a;b] b являє собою… |
|
8. Первісною функції xn, де n≠ -1, є… |
8. Первісною функції |
|
9. Первісною функції y=x -3 є… |
9. sin2xdx =… |
|
10. e 5xdx= |
10. Як знайти переміщення s точки за проміжок часу t1;t2, якщо відомо швидкість v(t) цієї точки? |
Експерти підбивають підсумки, учасники груп заповнюють картки самооцінки.
ІІ гейм «Поспішайте бачити»
Кожній команді пропонуються аркуші з готовими малюнками. Ви повинні записати лише формулу, за якою шукатиме площу заштрихованої фігури. Капітани подають сигнал, коли роботи усієї команди будуть у них в руках. Команда, яка першою впорається із завданням, пригощається шоколадною цукеркою (4 бали додатково).
Команда 1 Команда 2
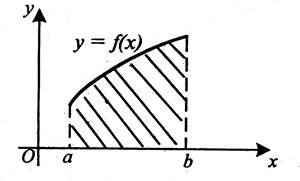
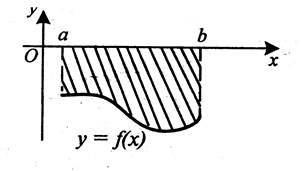
а) а)
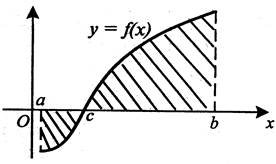
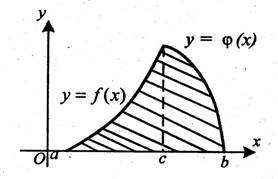
б) б)
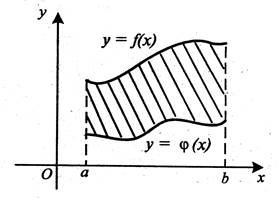
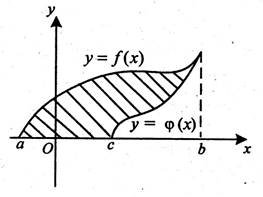
в) в)
Експерти підраховують бали.
ІІІ гейм «Швидке реагування»
Кожній команді видана практична задача на застосування похідної. Потрібно скласти задачу, обернену до даної, з використанням такої математичної операції як ін-
тегрування
Задача 1
Кількість електрики, що проходить через поперечний переріз провідника, змінюється за законом:
Q(t) = 2t2 +t (Кл)
Знайти силу стуму I(t) за 10 сек.
(I(t) = Q(t))
Обернена дія
Знайдемо спочатку похідну (закон зміни сили струму). Знаємо:
I(t) = Q(t) = 4t +1(А)
Обернена задача.
Сила струму змінюється за законом
I(t) = 4t +1 (А)
Знайти кількість електрики, що проходить через поперечний переріз провідника за 10 сек.
10
Q = (4t +1)dt = (2t2 +t)
100= 210 (Кл)
0
Задача 2
Знайти лінійну густину стержня (кг/м) завдовжки 0,2 м, якщо його маса змінюється за законом:
m(l) = 2l2 +3l (кг)
Обернена дія
Знаємо,
(l) = m(l) = 4l +3(кг/м)
Обернена задача.
Знайти масу стержня завдовжки 0,2 кг, якщо його лінійна густина змінюється за законом
(l) = 4l +3 (кг/м)
0,2
m(l) = (4l + 3)dl = (2l2 + 3l) 00,2 =
0
= 0,08+ 0,6 = 0,68 (кг)
Підведення підсумків ІІ і ІІІ геймів.
Загальна кількість балів: __________.
Учні відмічають свої досягнення у колективній роботі у картках самооцінки.
IV гейм «Казкова пригода»
Кожній команді, як домашнє завдання, необхідно було скласти казку з елементами задач, які розв’язувались би методами інтегрування. І запропоновані задачі буде розв’язувати інша команда. Подивимося, що у них вийшло.
Оцінюється оригінальність казки (4 бали) і вірність розв’язування задачі (4 ба-
ли).
Казка перша
Жив-був дід і було у нього три сини: два розумних, а третій – дурень. Зрозумів дід, що скоро вмиратиме, та й каже синам:
- Тобі, старший, залишаю дім і худобу. Тобі, середній, - землю. А тобі, молодший, - нічого, бо ти до діла нічого і робити не вмієш.
Образився Іван та й пішов куди очі дивляться й дійшов до царського палацу, а там указ читають:
- Хто знайде площу царства, обмежену лініями y = x2 − 4x + 4, y = 4− x, той на царівні жениться.
А Іван-дурень в школу не ходив, алгебру не вчив, а одружитися на царівні дуже
хочеться. Пішов він до лісу і зустрів там Бабу-Ягу, а вона і каже:
- Допоможу тобі, дурню, бо у місці була та й виміняла на мухомори формулу Ньютона-Лейбніца.
І розв’язала вона Івану задачу. y = x2 −4x + 4 = (x −2)2 - парабола, зміщена вправо на дві одиниці.
y = 4− x - пряма
Абсциси точок перетину: x2 −4x + 4 = 4− x x2 −3x = 0, x(x −3) = 0 x = 0 або x = 3
З’ясуємо, який графік вище по осі Oyдля x0;3.
x=1
y1 =1−41+ 4 =1
y2 = 4−1= 3,
отже, вище пряма
Будуємо задані лінії.
3 3 3
S = (y2(x)− y1(x))dx = (4 − x − x2 + 4x − 4)dx = (3x − x2)dx =
0 0 0
3
= 32x2 − x33 0 = 3232 − 333 =13,5−9 = 4,5 (м2)
Площа царства: 4,5 м2.
Хоч і маленьке придане, але Іван з радістю одружився.
Казка друга
Буває ж! Раніше оцінки діставали, а тепер он казки про первісну. А тут своїх проблем не обійти.
Купили ми нашому Шарику трактора, щоб він молоко від моєї корови в місто возив, грошики заробляв.
А він он на природу милуватися поїхав. Казав, що через 10 секунд повернеться,
а його ні слуху, ні духу. Бач, з’явився, не запилився.
- Ти, Шарику, у лісі трактора зупиняв?
- Ні.
- Так!
- Ні!
- Ну от! Ми його на смітнику знайшли, відмили, відкормили, а він нам бреше. А ну зізнавайся, з я кою швидкістю їхав?
v(t) = 4t −8 (м/с)
- Людоньки, допоможіть Шарика на чисту воду вивести. Доведіть, що зупиняв-
ся і знайдіть шлях, який він у лісі намотав.
Розв’язання
Якщо Шарик зупинявся, то
v = 0 4t −8 = 0 20;10
t = 2
Отже, зупинка була.
10 2 10
4t
S = 0 (4t −8)dt = 2 −8t 0 = 2100 −80 = 200 −80 =120 (м).
- Проштрафився ти, Шарику, тому будеш покараний: тепер на базарі купуватимемо тільки м’якоть, а тебе залишимо без сахарних кісточок.
Поки капітани розв’язують казкові задачі, ми впізнаємо невідомий об’єкт.
V гейм «Чорна скринька»
До вас на гру завітав невпізнаний математичний об’єкт. За 1-2 хв. ви повинні вказати, що це за об’єкт. Максимальна кількість балів для команди, що впізнає НМО – 3 бали.
Ось його опис.
Це одне з чудових ірраціональних чисел. Вивчаючи показникові функцію, ми зустрічалися з цим числом, - це була лише мить, але для логарифмічних функцій число має важливе значення. Похідні і первісні показникової функції, основою якої є це число, схожі між собою. Позначення цього числа запропонував Леонард Ейлер (1707 – 1803 р. р.). Називають його неперовим числом на честь шотландського математика Джона Непера (1550 – 1617 р. р.), який вперше склав таблиці, що стосуються до цього числа.
Якось на екзамені студент на запитання викладача: «Яке наближене значення цього числа?», - відразу дав відповідь, назвавши його до дев’яти знаків після коми. Коли викладач йому зауважив, що немає потреби обтяжувати свою пам'ять такою кількістю знаків – на практиці рідко використовують більше 3-4, – студент заявив, що запам’ятати це дуже легко: достатньо запам’ятати дві перших цифри, а далі – «двічі Лев Толстой».
Що це за число? Якщо зможете, назвіть його з такою ж точністю, з якою назвав винахідливий студент, а також похідну і первісну показникової функції, основою якої є це число.
(e 2,7 1828 1828)
рік народження Льва Толстого
Підведення підсумків IV і V геймів.
Загальна кількість балів.
Відмітки у аркушах самооцінки.
VI гейм «Обганялки» (додаток 2)
Команди навипередки повинні добути ключове слово, яке сховане у інтегральній скриньці. Для цього необхідно розв’язати п’ять різнорівневих завдань, які вам роздадуть експерти. Максимальна кількість балів: 14. Команда, яка першою впорається з завданням, додатково отримує карамельку. (3 бали)
Код перший: БРАВО (помилковий: білет); код другий: ВІТАЮ (помилковий:
вирок)
Оголошення результатів 6 гейма.
ІІІ. Підведення підсумків гри (уроку)
Експерти підраховують загальну кількість балів за гру і визначають переможця.
Учні виставляють собі оцінки у аркуші самооцінки. Оголошення оцінок за урок.
IV. Домашнє завдання
Підручник: Математика: (алгебра і початки аналізу та геометрія, рівень стандарту) 11 кл. / Олександр Істер, 2019
Виконати домашню самостійну роботу №2 на стр. 116 -117
Додаток 1
Аркуш самооцінки
|
П.І.Б. учня |
Гейм |
|
|
|
|
Сума «+» |
Оцінка |
||||||||||
|
І |
ІІ |
ІІІ |
IV |
V |
VI |
||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Додаток 2
Обганялки (І команда)
|
О |
e4 − 4e2 −1
2e2 |
|
Е |
2x3 + 2x2 −3x +1 |
|
Р |
7tgx −2cosx +C |
|
Л |
0 |
|
Б |
2x5 + 2x7 +C |
|
Т |
(e2 −1)2 2e2 |
|
А |
4 |
|
В |
2x3 + 2x2 −3x −1 |
|
І |
7tgx + 2cosx +C |
Інтегральна скринька
Знайдіть загальний вигляд первісної:
1) f (x) =10x4 +14x6 ; (2 бали)
2) f (x) = 
72 + 2sin x. (2 бали) cos x
Обчислити:
3
3) (2x −1)dx. (3 бали)
2
Знайти первісну функції
4) f (x) = 6x2 + 4x −3, якщо
F(−2) = −3. (3 бали)
Обчисліть
1
5) (ex −e−x)2dx. (4 бали)
0
Обганялки (ІІ команда)
|
О |
5x +3x2 −3x3 −7 |
|
І |
3sinx + 4ctgx +C |
|
Ю |
− 2
4 |
|
В |
4x3 − x6 +C |
|
Р |
4 |
|
А |
5x +3x2 −3x3 +7 |
|
Т |
- 4 |
|
И |
3sinx −4ctgx +C |
|
К |
+ 2
4 |
Інтегральна скринька
Знайдіть загальний вигляд первісної:
1) f (x) =12x2 −6x5 ; (2 бали)
2) f (x) = 3cos x − 
[1]2 . (2 бали) sin x
Обчислити
2
3) (2x −3x2 )dx. (3 бали)
1
Знайти первісну функції
4) f (x) = [2]+ 6x −9x2 , якщо
F(−3) =100. (3 бали)
Обчислити:
0
про публікацію авторської розробки
Додати розробку