Урок: " Піраміда. Елементи піраміди. Види пірамід."

 

 Тема заняття: Піраміда. Елементи піраміди. Види            пірамід.

 

Мета заняття: формувати поняття піраміди, правильної та зрізаної та їх елементів. Засвоїти властивості правильних пірамід, формули для обчислення площі повної та бічної поверхні піраміди. Розвивати творчу та пізнавальну активність студентів, уміння робити висновки на основі даних, отриманих під час досліджень. Виховувати в студентів бажання до самовдосконалення.

Тип заняття: Лекція (презентація проектів).

Вид заняття: Інтерактивний.

Обладнання: Мультимедійний проектор, екран, моделі пірамід.

Міжпредметні зв’язки:

• фізика – тема – «Закон збереження енергії»;
• астрономія – тема – «Закони руху планет»;
• географія  – тема – «Країни Африки»;
• художня культура – тема – «Архітектура  України».

Епіграф: Все на землі боїться часу, і тільки час боїться пірамід.

Хід заняття

1.Організаційна частина.

2.Самостійна робота.

    І варіант.

1) Якщо кожне ребро правильної шестикутної призми дорівнює а, то площа її бічної поверхні дорівнює:

а) 2а²; б) 4а²; в) 6а²; г) 8а².

2) Якщо ребро куба дорівнює 3см, то його площа поверхні дорівнює:

а) 9см²; б) 36см²; в) 54см²; г) 27см².

3) Якщо виміри прямокутного паралелепіпеда дорівнюють 8см, 9см і 12см, то його діагональ дорівнює:

а) 12см; б) 17см; в) 20см; г) 29см.

4) Якщо площі деяких граней паралелепіпеда дорівнюють 2см²,3см². 6см², то його повна поверхня дорівнює:

а) 11см²;б) 36см²; в) 100 см²; г) 22см².

5) Якщо площа діагонального перерізу куба дорівнює Q, то його поверхня дорівнює:

а) √2Q; б) √3Q; в) 2√3Q; г) 3√2Q.

6) Якщо ребро куба збільшити у 2 рази, то площа поверхні збільшиться:

а) у 4 рази; б) у 2 рази; в) у 3 рази; г) у 6 раз.

ІІ варіант.

1) Якщо кожне ребро правильної восьмикутної призми дорівнює а, то площа її бічної поверхні дорівнює:

а) 2а²; б) 4а²; в) 6а²; г) 8а².

2) Якщо поверхня куба дорівнює 24см², то його ребро дорівнює:

а) 2см; б) 3см; в) 4см; г) 6см.

3) Якщо виміри прямокутного паралелепіпеда дорівнюють 12см, 16см і 21см, то його діагональ дорівнює:

а) 23см; б) 25см; в) 27см; г) 29см.

4) Якщо площі деяких граней паралелепіпеда дорівнюють 2см², 5см² і 6см², то його повна поверхня дорівнює:

а) 13см²;б) 26см²; в) 39 см²; г) 52см².

5) Якщо діагональ куба дорівнює d, то його повна поверхня дорівнює:

а) d²; б) 2d²; в) 3d²; г) √3d².

6) Якщо ребро куба збільшити на 2см, то його повна площа поверхні збільшиться:

а) на 4 см²; б) на 8 см²; в) на 4√2см²; г) визначити не можливо.

Студенти письмово відповідають на запитання.

Перевірку здійснити в парах.

3.Вступне слово викладача.

   Мотивація навчальної діяльності

   Наше заняття  сьогодні незвичайне і присвячене воно знайомому і в той же час загадковому геометричному тілу – піраміді. Понад п’ять тисячоліть назад була споруджена перша піраміда – колосальна гора з каменю, побудована на точному математичному розрахунку. З тих пір вивченням пірамід займалися історики, археологи, географи. І ми з вами сьогодні будемо вивчати піраміди.

    З цією метою було створено дві групи. Група «Історики» повинна була знайти матеріали про перші піраміди і підготувати слайди із їх зображенням.

 

Група «Дослідники» повинна була дослідити піраміди з математичної точки зору, розглянути унікальні властивості пірамід і підготувати матеріал про практичне використання цих властивостей.

Піраміди мають багато секретів і таємниць. Але, насамперед, піраміди, а точніше єгипетські піраміди – це одне із семи чудес світу.   

 

 Чому їх вважають чудом?  Чудом  піраміди вважають за їхню могутність, за їхню велич, за те, що на їхню будову були витрачені величезні кошти, а ще за їх вік. «Все на землі боїться часу, і тільки час боїться пірамід» - говорить арабська приказка. Ці слова будуть епіграфом до нашого заняття. На ньому ми постараємося за допомогою ваших досліджень та робіт розкрити таємниці пірамід і здобути знання, які не тільки розширять ваш кругозір, а й будуть необхідні при розв’язуванні практичних задач. Тож запрошую групу істориків.

4. Повідомлення групи істориків.

 (виступ групи істориків)

Одне із семи чудес світу — єгипетські піраміди. (слайд 2)

                    

  Довгий час вважалося, що піраміда — це будова релігійного характеру. Єгиптяни вірили, що смерть – це не кінець існування людини. Стародавній єгиптянин міг сподіватися на загробне життя лише в тому разі, коли будуть виконані дві важливі умови: по-перше,його тіло мало зберегтися цілим і неушкодженим, і,по-друге, його душа мала одержати все потрібне для життя на тім світі. З цього прагнення зберегти тіло походить звичай муміфікації мертвих. Первісні прості  обмуровані ями в піску, що мали забезпечити муміфіковане тіло від різних ушкоджень,  змінилися з часом у так звані мастаби (слайд 3). 

 

 

 

 

 

 

 

 Гробниці царів мали бути найбільшими, найміцнішими, з найбагатшими пожитками. Тому з часом вони розвинулися з мастаб  в піраміди.

До наших часів збереглося біля сім­десяти пірамід. (Слайд 4, 5, 6)

 

 

 

                                           

 

 

 

Колись їх було ще біль­ше; але деякі з них зруйнував всевлад­ний плин часу, інші засипало море піску, що насунулося з пустелі. Скільки їх загалом побудували єгиптяни, визна­чити важко. На скелястому плоскогір'ї, що відокремлює долину життєдайного Нілу від мертвої пустелі, височіють вони, ви­шикувавшись  в  ряд  на  шістдесят  п'ять кілометрів від Каїра до Фаюму, мов на велетенському плацу, де їм щоденно ро­бить огляд єгипетський бог сонця. (Слайд 7)

 

 

 

 

   Піраміда має дуже просту геометрич­ну форму (слайд 8).

 

 

 

Назву її одні виводять від гре­цького слова «пір», що означає «вогонь» (бо полум'я має вигляд гостроверхої піраміди) інші від слова «пірос» тобто пшениця. Нам здається, що походження цього слова треба шукати у староєгипетському «п-р-м-в-с», тобто «пірамеус» (стародавні єгиптяни, як і сучасні їхні арабські нащадки, не писали голос­них).  Піраміда – ідеально – пропорційна модель всіх природних процесів життя, про яку знаменитий і славетний грецький філософ Піфагор, після досить тривалої (22 роки) подорожі Єгиптом, залишив загадковий напис: «Секрет Всесвіту».

    Та не всі піраміди мають правильну геометричну форму Найстарша з них — «східчаста піраміда» біля Саккари, збу­дована царем Джосером приблизно в 2670 року до нашої ери. (Слайд 9) Фараон Снофру, батько Хеопса,

побудував першу піраміду з рівними стінами — Рожеву піраміду (слайд 10).

       

Біля Медума є зрізана східчаста пі­раміда, біля Дахшура піраміда із злама­ним обрисом (слайд 11)

 

 

 

 

 Поміж пірамід є навіть одна кругла, але всі єгипетські піраміди, що їх залі­чують до чудес світу, мають правильну геометричну форму з квадратною осно­вою і подібні одна до одної, мов близ­нята.

        Великими пірамідами називають розташовані в Гізі піраміди фараонів Хеопса (Хуфу) (слайд 12), Хефрена (слайд 13) і Мікерина (слайд 14).

                         

 

 

 

 На відміну від піраміди Джосера, ці піраміди мають не ступеневу, а суворо геометричну, пірамідальну форму.

Але що найдужче дивує відвідувачів пірамід біля Гізи  це технічні досягнення будівників пірамід. «Важко збагнути, у який спосіб могли підняти таку силу кам'яних брил на таку височінь»,— говорить Філон і має рацію. На­віть і тепер, коли ми знаємо, як будувались піраміди, коли маємо перед очима досягнення нашого високомеханізованого будівництва, це викликає наш подив. Адже найменша брила з Хеопсової піраміди важить

 2 000 кілограмів,  а найбільша  аж 40 000  кілограмів! (Слайд 15)    

 

 

 

 

 

 

 

 

 

   Розміри піраміди, система підземних коридорів, поховальна ка­мера, зовнішня кладка піраміди — усе це свідчить про надзвичайну технічну майстерність єги­петських будівельників. (Слайд 16,17,18,19)

 

               

 

 

 

 

 Точна орієнтація пірамід за сторонами світу й між собою (наприклад, діагональ Хеопсової піраміди з північного сходу на південний захід точно збігається з продовженням діагоналі Хефренової піраміди(слайд 20) свідчить у свою чергу про виняткові знання єгипетських астрономів та геометрів.

  Але хоч як дивують нас їхні досягнення, проте це захоплення поступається перед іншим, коли ми звернемо увагу на майже непомітну дрібницю: камінні бри­ли на стінах похоронної камери так точно витесані й так щільно при­пасовані одна до одної, що між ними не встромиш навіть ріжок то­ненького паперу!

 

 

 

 

 

  І ця досконала точність і майстерність, яка виявляється в кожній  деталі (слайд 21,22,23),-

 

 

 

 

 

 це вже не досягнення інженерів, а сірої, безіменної, знедоленої і поневоленої маси людей, що орудували лише примітивним мідним знаряддям і шліфували брили тільки вручну, піском і водою!

      Якщо числа можуть часом, як і вірші поетів, збуджувати уяву, то до таких

саме чисел, безумовно, відносяться виміри Великої піраміди.(Слайд 24)

 

 

 

 

 

 

 

 

 

      Від основи до вершини ця камінна гора має 147 метрів. За давніх часів вона була на десять-одинадцять метрів вища, її шпиль невідомо коли розкришився, і тепер на цьому місці є невеличкий майданчик, на якому під час другої світової війни містився англійський пост протиповітряної оборони. Бік її квадратної основи має 234 метри. Кубатура Великої піраміди — знаючи формулу, вирахувати її дуже легко — дорівнює  приблизно  2 600 000  кубічних  метрів. На будову піраміди використано приблизно 2 300 000 камінних брил, кожна об'ємом у середньому більше одного кубічного метра і вагою приблизно дві з половиною тонни.

    Фантастичні числа! А тепер розшифруймо їх.

Площа основи має понад 54 000 квадратних метрів, тобто 5,4 гек­тара. П'ять гектарів — це площа досить значного селянського госпо­дарства.

 

На цій площі вмістилося б 10 000 двокімнатних квартир з усіма вигодами. Таких вілл, яку звелів збудувати біля цієї піра­міди останній єгипетський

король Фарук, вмістилося б там зо дві сотні, Серед імператорів і королів Європи навіть найбагатші й наймогутніші не мали такого палацу, який забудованою площею дорів­нював би цій фараоновій гробниці:(слайд 25)

 

 

 

 

 

 Букінгемський палац у Лондо­ні менший, менші Версаль і колишній царський Зимовий палац.

Хеопсова піраміда вища, ніж баня Мікеланджело над собором святого Петра в Римі, який вважається найбільшим християнським храмом. Якби ця піраміда була порожня, у ній помістилася б стар­това площадка  ракетодрому разом із  космічною  ракетою.

Після Хеопса ніхто не спромігся спорудити величнішого символу необмеженої влади фараона. Подивіться, що залишилося від деяких пірамід (слайд 26-34).

 

                                

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  Проте і сьогодні у Хеопсовій піраміді дивує все: і її розміри, і її форма і навіть те, в який спосіб злодіям пощастило пробратися в середину. І тому Велика піраміда  - справді чудо світу. (слайд 35-36).

 

     

 

 

 

 

 

 

5. Повідомлення групи дослідників.

Властивості пірамід

(виступ групи дослідників)

У стародавньому Єгипті було споруджено славнозвісні єгипетські піраміди.

(слайд1-2)

 

 

 

 

 

 

 До останнього часу вважалося, що це - величні гробниці, останній притулок фараонів. Однак тепер вчені наполягають на тому, що функції пірамід набагато ширші.

 

Про це говорять і дивовижні результати вимірювання піраміди Хеопса.

( слайд 3-5)

 

 

 

 

 

 

 

 

 

 Діагональ однієї з граней направлена ​​по меридіану точно на Північний полюс. Крім того, з'ясувалося, що єгипетські майстри зробили піраміди відображенням розташування зірок у сузір'ї Оріона, а вершина Великої піраміди дивиться точно на Полярну зірку.

Крім цього:

• Периметр підстави піраміди Хеопса, поділений на подвоєну висоту дає наближення числа «Пі» - 3,1415 .(слайд6)

 

 

 

 

 

 

 

• Периметр підстави піраміди дорівнює довжині кола, радіус якого дорівнює висоті піраміди
• Довжина сторони підстави, виражена в єгипетських «ліктях» , відповідає тривалості земного року.

 

• Якщо помножити початкову висоту Великої Піраміди - 146,6 м на один мільйон, виходить найменша відстань від Землі до Сонця - 147000000 км (перигелій).

• Площа кожної з граней піраміди дорівнює квадрату її висоти.
  Невже така вражаюча точність  була необхідна тільки для поховання фараона?

Тому,за однією з теорій, піраміди - це найпотужніший енергетичний центр Землі. Розташування піраміди Хеопса в цьому сенсі унікально: меридіан, на якому розташована її вершина, ділить поверхню суші та моря порівну, включаючи Америку і Тихий океан, і більш того, паралель, що проходить

через центр піраміди, також ділить планету на дві рівні частини за кількістю води і суші. (слайд7)

 

 

 

 

 

 

    Вчені виявили, що енергія піраміди має багато унікальних властивостей: розчинна кава, яка деякий час перебувала під її впливом, набуває смаку натуральної; дешеве вино значно поліпшує свої смакові якості; вода отримує властивість заживляти рани, тонізує організм, зменшує запальну реакцію

 

після укусів, опіків, покращує травлення; м'ясо, риба, яйця, фрукти муміфікуються, але не псуються; молоко довго не кисне; сир не пліснявіє.

(слайд8-10)

 

 

 

Якщо сидіти в піраміді, зменшується інтенсивність головного і зубного болю, пришвидшується заживання ран і виразок.(слайд 11-12)

 

 

 

 

 

 

 

І так діє не лише піраміда Хеопса. Кожен може виготовити собі піраміду.

Але, щоб  модель піраміди використовувалась у технології оздоровлення, вона повинна бути правильної геометричної форми її грані повинні бути орієнтовані за сторонами світу, вона не повинна  контактування з приладами, які мають сильні електромагнітні випромінювання.

  Отож, корисна дія піраміди на організм людини та навколишнє середовище така:

- нормалізація кров'яного тиску;

- зняття стресового стану людини;

- лікування артриту та ревматизму, болю зубів;

- позбавлення відчуття втоми;

 

- поліпшення сну;

- поліпшення біополя людини та навколишнього середовища;

- підвищення концентрації уваги під час навчання, творчої чи фізичної роботи;

- підвищення та активація сенсорних та чуттєвих систем людини;

- підвищення фізичної активності людини;

- підвищення активності імунної системи людини і тварини;

- підвищення екстрасенсорних властивостей у людей, які схильні до них.

При обробці насіння сільськогосподарських культур в піраміді підвищується його врожайність на ЗО-70 %.(слайд 13-14)

 

 

 

 

 

 

 

 

 

  Алмази, синтезовані із графіту, який пролежав тиждень в піраміді, більш чисті, твердіші, досконаліші за формою. Вода, яка стояла в піраміді, не змінює своїх властивостей роками. Нафта змінює свій склад, якщо на поверхні встановлені піраміди. Паличка мишачого тифу у 35-40 % мишей,, які перед зараженням знаходилися в піраміді,не викликає смерті.

Як це все пояснити?

  Єгиптологом М. В. Сарятином (1883-1963) було досліджено, що піраміди є джерелами випромінювання. Випромінювання піраміди має складну структуру і особливі властивості. Вченим було виявлено декілька променів:

 

- промінь (пі), під впливом якого відбувається руйнування пухлинних клітин;

- промінь, який спричиняє муміфікацію (висушування) і знищення мікроорганізмів;

- таємний промінь Омега, під впливом якого продукти довгий час не псуються і який має благотворний вплив на організм людини(слайд15-17)

 

 

 

 

 

 

 

 

 Ці та інші відомості про піраміди змушують вчених вивчати особливості пірамід. (слайд18-20)

 

 

 

 

 

 

 

 

Проте, з кожним новим дослідженням виникає більше нових питань, ніж відповідей. Тож сьогодні доводиться визнати лиш одне : єгипетські піраміди являють собою дивовижний приклад геометричної і математичної містики.

 

 

 

6.Пояснення нового матеріалу

    Слайд1- 2.

 

 

 

 

 

 

        В житті ми часто зустрічаємось з пірамідами. Проте при слові «піраміда» уява зразу ж малює картинку, на якій красується піраміда Хеопса. (Слайд 3). Мабуть дуже мало є на землі людей, які б ніколи про неї не чули. Ще 2-3 тисячі років до нашої ери форми пірамід використовувалися у побудовах гробниць для фараонів. Проте, піраміди це не лише усипальниці.

 Слайд 3-4.

 

 

 

 

 

 

 У 1776 р. Конгресом США було прийнято ескіз державної печатки зі зрізаною пірамідою. Якщо подивитися на американську купюру в один долар, то на її звороті й нині можна побачити зрізану піраміду.

 Слайд 5.

 

 

 

 

 

 

 

 

 

 Дизайнери, архітектори використовують пірамідальні форми при побудові будинків, ліхтарів на вулицях.

 Слайд 6.

 

 

 

 

 

 У вигляді шести – і восьмигранних пірамід будують каплички, церкви.

           Слайд 7.

 

 

 

 

      Форму правильних восьмикутних пірамід мають гострокінцеві дахи на баштах.

 Слайд 8.

 

 

 

 

 

        Дахи пірамідальної форми прикрашають різні кіоски, альтанки, грибочки на пляжі.

 Слайд 9.

 

 

 

 

       Бункери для піску або розчину, що застосовують на будівництві і в промисловості, часто роблять у формі зрізаної чотирикутної піраміди.

 

Слайд 10.

 

 

 

 

 

 

Пірамідальні форми використовують для виготовлення предметів побуту.

 

 

Слайд 11.

 

 

 

 

       Використовуються вони і при виготовленні упаковки для продуктів у харчовій промисловості. Ми купуємо пакетики чаю у вигляді пірамід.

 

       Слайд 12.

 

 

 

 

 Упаковка томатної пасти теж для зручності має форму піраміди.

 Слайд 13.

 

 

 

 

 

       Весь світ знає піраміду Рубіка і головоломку «Піраміда».

 Слайд 14.

 

 

 

 

 

        А діти складають іграшкові пірамідки, пірамідки із камінців і доміно.

 Слайд 15.

 

 

 

 

 

 

   Навколишній світ – це світ геометрії, чистий, істинний, бездоганний в наших очах. Усе навколо геометрія.

 Слайд 16.

 

 

 

 

 

     Та все ж. піраміда – це насамперед геометричне тіло, це многогранник. Можна дати такі визначення піраміди.

 Слайд 17.

 

 

 

 

 

   Пірамідою називається многогранник, що складається з плоского многокутника – основи піраміди, точки, яка не належить площині основи – вершини піраміди, та всіх відрізків, що сполучають вершину піраміди з точками основи.

 

         Слайд 18.

 

 

 

 

 

 Інше визначення: піраміда – це многогранник, одна грань якого – довільний многокутник, а інші грані – трикутники, що мають спільну вершину.

 Слайд 19.

 

 

 

 

 

 

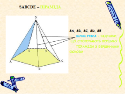
 Спільну вершину трикутних граней називають вершиною піраміди, а протилежну їй грань – основою.

 

Слайд 20.

 

 

 

 

 

      Відрізки, що сполучають вершину піраміди з вершинами основи називають ребрами піраміди.

 

         Слайд 21.

 

 

 

 

 

 

 

 

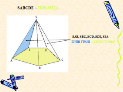
 Бічні грані пірамід – трикутники.

 Слайд 22.

 

 

 

 

 

 

 

  Висота піраміди – це перпендикуляр опущений з вершини піраміди на площину основи. Висотою називають і довжину цього перпендикуляра.

 

       Слайд 23.

 

 

 

 

 

 

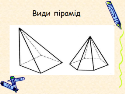
      Назва піраміди залежить від кількості сторін у многокутнику, який лежить в основі піраміди.

 

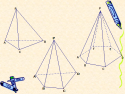
Слайд 24.

 

 

 

 

     Перед вами трикутна, чотирикутна і шестикутна піраміди.

 

Слайд 25.

 

 

 

 

 

Трикутну піраміду часто називають тетраедром.

 

 Слайди 26-28.

 

 

 

 

 

 

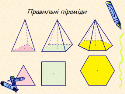
 Серед пірамід виділяють правильні піраміди.

 Піраміда називається правильною, якщо в її основі лежить правильний многокутник і всі бічні ребра рівні між собою. Можна дати і інше означення. Піраміда, в основі якої лежить правильний многокутник і основа висоти піраміди збігається з центром цього многокутника теж називається правильною.

 

 Перед вами правильні трикутна, чотирикутна і шестикутна піраміди.

 Слайд 29.

 

 

 

 

 

 

 Висота бічної грані, проведена з вершини правильної піраміди називається апофемою.

 Слайди 30-31.

 

 

 

 

 

 

    Площина, яка паралельна основі піраміди й перетинає її, відтинає подібну фігуру. Друга частина фігури – це многогранник, який називається зрізана піраміда.

 Зрізана піраміда, яку дістали з правильної піраміди називається правильною зрізаною пірамідою.

 

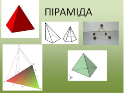Слайд 32.

 

 

 

 

      А тепер я розповім вам про властивості пірамід,щоб  підготувати вас до розв’язування задач.

Слайд 33.

 

 

 

 

 

     Насамперед, декілька слів про основні елементи піраміди (про деякі ви вже чули). Перед нами п’ятикутна піраміда SABCDE. Основа піраміди, висота, бічні ребра, бічні грані, апофема. У піраміді є декілька видів кутів: плоский кут при вершині, кут нахилу бічного ребра до площини основи, двогранний кут при бічному ребрі та кут нахилу бічної грані до площини

 

основи.

Ми знаємо, що для призми має місце теорема Ейлера: в+г-р=2. Чи справедлива ця теорема для піраміди? Давайте встановимо залежність між назвою піраміди і кількістю в ній ребер, вершин і граней.

Слайд 34.

 

 

 

 

     Перевірте чи немає помилок в нашій таблиці. Тобто теорема Ейлера має          місце і для пірамід. Подумайте і скажіть чи існує піраміда в якої 55 ребер?

 Перш ніж розв’язувати задачі, потрібно навчитися будувати зображення

пірамід. Але спочатку побудуйте піраміди за допомогою стереометричних ящиків( учні працюють із стереометричними ящиками за індивідуальними завданнями, озвучують результати).

Слайд 35-37.

 

 

 

 

 

 

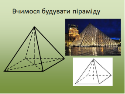
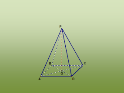
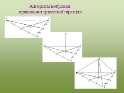
 Подивіться як будувати зображення правильної чотирикутної піраміди.

А так будується зображення правильної трикутної піраміди.

 Запам’ятайте: Основа висоти в правильній трикутній піраміді співпадає

з точкою перетину медіан трикутника, який лежить в основі піраміди; основа висоти в правильній чотирикутній, шестикутній пірамідах співпадає з точкою

перетину діагоналей многокутника, що лежить в основі піраміди.

 

 

 

Слайд 8.

 

 

 

 

 

   А тепер ми хочемо познайомити вас з деякими видами пірамід.

Слайд 9.

 

 

 

 

 

 Піраміди в яких основа висоти лежить у центрі кола, вписаного в основу.

Слайд 10.

 

 

 

 

 

 

Піраміди в яких основа висоти є центром кола, описаного навколо основи.

Слайд 11.

 

 

 

 

 Піраміди, в яких дві суміжні бічні грані перпендикулярні до площини основи (бічне ребро перпендикулярне до площини основи і є висотою піраміди).

Піраміди, в яких одна бічна грань перпендикулярна до площини основи (висотою піраміди буде висота цієї грані).

Слайд 12.

 

 

 

 

 

      Ми вивчили тему «Призми», познайомилися з пірамідами. Порівняйте ці многогранники.

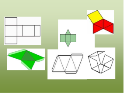Слайд 13.

 

 

 

 

 

 Порівняйте їх розгортки. Скільки розгорток пірамід ви бачите. Пригадайте як знайти площу поверхні призми.

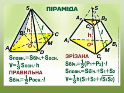Слайд 14

 

 

 

 

 

 

 

 

 Запамятайте  ці формули!

Я надіюсь, що отримані знання допоможуть вам у розв’язуванні задач.

7. Закріплення вивченого матеріалу.

 Виконання студентами тестів (відповіді «так» і «ні»):

1)  Чи існує піраміда, яка має 125 ребер?

2)  Чи існує піраміда, яка має 125 граней?

-3) Чи  може піраміда мати дві бічні грані, перпендикулярні до основи?

4)  Якщо в піраміді бічні ребра утворюють з висотою рівні кути, чи                                      проектується  її вершина в центр кола, вписаного в основу?         

5) Якщо висоти всіх бічних граней, проведені із вершини піраміди, рівні, чи буде основа висоти центром кола, вписаного в основу?

6) Якщо бічні ребра піраміди рівні і в основі лежить тупокутній трикутник, чи буде основа висоти лежати поза основою?

7)  Якщо бічні ребра піраміди рівні і в основі лежить прямокутний трикутник, чи буде основа висоти лежати всередині основи піраміди?

8) Чи може піраміда мати три бічні грані, перпендикулярні до площини основи?

9) Якщо одна з бічних граней піраміди перпендикулярна до основи, чи збігається висота піраміди з висотою однієї грані?

10)  Чи може піраміда мати два бічні ребра, перпендикулярні до основи?

11) Чи існує піраміда, яка має 18 плоских кутів?

12) Чи можуть бути рівними бічні ребра піраміди, якщо в її основі лежить трапеція?

8. Підсумок заняття, виставлення оцінок( тести, робота в групах).

9. Домашнє завдання. п.22, №№798, 801, 805, 807.

 

 

 

 

П.І.Б.___________________________________________________________

Самостійна робота

  І варіант.

1) Якщо кожне ребро правильної шестикутної призми дорівнює а, то площа її бічної поверхні дорівнює:

а) 2а²; б) 4а²; в) 6а²; г) 8а².

2) Якщо ребро куба дорівнює 3см, то його площа поверхні дорівнює:

а) 9см²; б) 36см²; в) 54см²; г) 27см².

3) Якщо виміри прямокутного паралелепіпеда дорівнюють 8см, 9см і 12см, то його діагональ дорівнює:

а) 12см; б) 17см; в) 20см; г) 29см.

4) Якщо площі деяких граней паралелепіпеда дорівнюють 2см²,3см². 6см², то його повна поверхня дорівнює:

а) 11см²;б) 36см²; в) 100 см²; г) 22см².

5) Якщо площа діагонального перерізу куба дорівнює Q, то його поверхня дорівнює:

а);  б) ; в)2; г) 3.

6) Якщо ребро куба збільшити у 2 рази, то площа поверхні збільшиться:

а) у 4 рази; б) у 2 рази; в) у 3 рази; г) у 6 раз.

	А	Б	В	Г
1.
2.
3.
4.
5.
6.

 

Ланцюжок відповідей на тести

1

2

3

4

5

6

7

8

9

10

11

12

 

 

 

П.І.Б.___________________________________________________________

Самостійна робота

ІІ варіант.

1) Якщо кожне ребро правильної восьмикутної призми дорівнює а, то площа її бічної поверхні дорівнює:

а) 2а²; б) 4а²; в) 6а²; г) 8а².

2) Якщо поверхня куба дорівнює 24см², то його ребро дорівнює:

а) 2см; б) 3см; в) 4см; г) 6см.

3) Якщо виміри прямокутного паралелепіпеда дорівнюють 12см, 16см і 21см, то його діагональ дорівнює:

а) 23см; б) 25см; в) 27см; г) 29см.

4) Якщо площі деяких граней паралелепіпеда дорівнюють 2см², 5см² і 6см², то його повна поверхня дорівнює:

а) 13см²;б) 26см²; в) 39 см²; г) 52см².

5) Якщо діагональ куба дорівнює d, то його повна поверхня дорівнює:

а) d²; б) 2d²; в) 3d²; г) √3d².

6) Якщо ребро куба збільшити на 2см, то його повна площа поверхні збільшиться:

а) на 4 см²; б) на 8 см²; в) на 4√2см²; г) визначити не можливо.

	А	Б	В	Г
1.
2.
3.
4.
5.
6.

 

Ланцюжок відповідей на тести

1

2

3

4

5

6

7

8

9

10

11

12