Урок "Властивості рівнобедреного трикутника"

   Урок

Тема: Рівнобедрений трикутник та його властивості.

Мета:

• Ввести поняття рівнобедреного трикутника. Засобами дослідницької діяльності сформулювати і довести властивість рівнобедреного трикутника. Навчити учнів розрізняти рівнобедрений трикутник серед інших, сприяти розумінню та застосуванню властивості рівнобедреного трикутника для розв'язування задач.
• Розвивати просторове уявлення, пізнавальну активність учнів, самостійність мислення, вміння аналізувати відповіді однокласників, доводити власну точку зору.
• Виховувати активну позицію в навчанні, здатність відстоювати   свою думку, готовність до співпраці.

Тип уроку: Засвоєння нових знань, умінь і навичок.

Обладнання: Креслярські інструменти, мультимедійний проектор, моделі рівнобедрених трикутників, моделі квіток для рефлексії, червоні та зелені картки для гри «Вірю – не вірю», картки і плакат з домашнім завданням.

 Розум людський має три ключі,

 які все відчинять: знання,

 думка, уява – все у цьому.

В.Гюго

                                    Хід уроку

І. Організаційний етап. Повідомлення теми уроку. Мотивація навчальної діяльності.

Сьогоднішній урок пройде під впливом сузір’я північної півкулі Трикутник, що займає площу 132 квадратних градуса та складається з 25 зірок, які видно неозброєним оком.

ІІ. Рефлексія.

На спеціально підготовлених паперових квітках учні пишуть свої очікування від сьогоднішнього уроку, бажаючі учні озвучують вголос написані бажання.

ІІІ. Актуалізація опорних знань.

Гра «Вірю – не вірю».

Учні отримують картки червоного та зеленого кольорів. Після кожного твердження учні піднімають картки: зелену, якщо правильно і червону, якщо не правильно.

Запитання 

1. _ΔPQT – рівнобедрений.                  
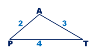
2. FD - висота _ΔEFG     
3. PS – бісектриса _ΔRPT   
4. P(_ΔKLM) =18см,  KL=10см 
5. PN – висота _ΔSPT
6. _ΔABK=_ΔACK – за ІІ ознакою рівності трикутників
7. DC = 10 см 
8. Трикутники рівні за І ознакою рівності трикутників 
9. P(_ΔABC) = 25 см,  AB = 9 см 
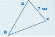
10. ST – медіана _ΔQSR 

ІV. Вивчення нового матеріалу.

1. Дослідження проблеми.

     Геометричне орігамі.  (Робота в групах з різними видами рівнобедрених трикутників.)

1. Знайдіть на своїй моделі рівнобедреного трикутника однакові на ваш погляд елементи, назвіть їх. Яким чином можна пересвідчитись в їх рівності за допомогою моделі?
2. Зігніть модель трикутника таким чином, щоб співпали рівні сторони. Які ще елементи виявилися однаковими?
3. Сформулюйте висновки.

2. Доведення властивостей рівнобедреного трикутника.

V. Первинне засвоєння матеріалу.  Мені цікаво, чи подужаєте ви розв’язати наступні задачі

VI. Учнівські доробки. 

1. Звіт групи теоретиків, які досліджували історію питання.
2. Звіт групи практиків, які досліджували практичне застосування рівнобедрених трикутників.

VII. Рефлексія.

Запитати учнів, чи справдилися їх очікування на уроці, чи отримали вони бажане, якщо так, то покласти квітку із записаними очікуваннями на уроці на воду, побачити, як вона розквітне.

VIII. Підсумки уроку.

Висновки.

IX. Домашнє завдання.

1. Вивчити §13.  
2. Знайти помилку в доведенні твердження, що будь-який трикутник є рівнобедреним.

Доведення.

Нехай АВС – довільний трикутник; побудуємо в ньому бісектрису ےА та перпендикуляр до сторони ВС в її середині D. Ці дві лінії – бісектриса та серединний перпендикуляр перетинаються в точці О,  яку ми з’єднуємо відрізками з вершинами трикутника – точками В і С, а також опускаємо з точки О перпендикуляри OF і OE на AB і на AC відповідно. Тепер маємо   ΔAFO=ΔAEO – за другою ознакою  рівності трикутників,  ΔODB=ΔODC -– за першою ознакою  рівності трикутників. Звідси маємо, що OF=OE і OB=OC, значить,  ΔOBF=ΔOCE. Відповідно до доведеного, маємо AF=AE, FB=EC, звідки шляхом   додавання отримуємо шуканий результат: AB=AC, тобто ΔАВС – рівнобедрений.