Урок "Площа бічної і повної поверхні циліндра"

Урок з геометрії в 11 класі з елементом кейсу

Тема: Площа бічної і повної поверхні циліндра.

Цілі уроку: 

• формування поняття площі поверхні; вивчення формули для площі бічної поверхні циліндра, а також умінь знаходити площу поверхні циліндра.
• Розвивати просторову уяву, вміння логічно аргументувати та розвивати тему, формулювати висновок, чітко будувати свою відповідь.
• Виховувати   зібраність, самовладання, комунікативність.

Обладнання: кейс з циліндром.

Структура уроку:

І. Організаційний етап.   3 хв

ІІ. Перевірка домашнього завдання 5 хв

III. Сприйняття та усвідомлення нового матеріалу 15 хв

IV. Закріплення нового матеріалу 15 хв

V. Домашнє завдання   3 хв

VІ. Підведення підсумку уроку  4 хв

Хід уроку

І. Організаційний етап. Клас можна поділити на групи по 4-5 чоловік (або якщо клас невеликий, то можлива індивідуальна робота).

ІІ. Перевірка домашнього завдання

III. Сприйняття та усвідомлення нового матеріалу

Кейс надається групам безпосередньо на занятті, організовується робота вгрупах з пошуку рішення поставленої проблеми і використання її длядосягнення поставленого завдання.На дослідження питання і роботу з кейсомвідводиться близько 15 хвилин часу заняття.

Завдання до класу:

1. Визначити, скільки тканини потрібно для виготовлення такого циліндра;
2. Визначити, від чого залежить витрата тканини.

Очікуваний план дій учнів:

1. Учні отримали кейс, виконують заміри (висота циліндра, радіус плоскої основи та радіус кільця).
2. «Розбити» циліндр на складові: круг, прямокутник та кільце.
3. Знайти площі цих фігур.
4. Зробити висновок.

Після дослідницької роботи учнів вчитель доповнює отримані знання.

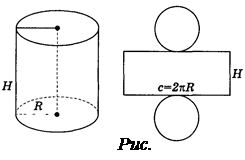Площа поверхні циліндра

Поверхня циліндра складається з двох рівних основ і бічної поверхні. Якщо поверхню циліндра розрізати по колах основ і якій-небудь твір­ній, а потім розгорнути на площині, то дістанемо розгортку циліндра (рис. 167). Вона складається з прямокутника, сторони якого дорівнюють довжині кола основи циліндра і його висоті, і двох кругів, що дорівню­ють основам циліндра.

Площею бічної і повної поверхні циліндра називають площу розгортки бічної і повної поверхні. Тоді площа бічної поверхні S_біч і пло­ща повної поверхні S_цил визначаються формулами:

S_біч = 2πRH,

S_цил = 2πRH + 2πR² = 2πR(H + R), де R, Н — радіус і висота циліндра відповідно.

IV. Закріплення нового матеріалу 

1.   Діаметр циліндра дорівнює 1 см, а висота дорівнює довжині кола основи. Знайдіть площу бічної поверхні циліндра. (Відповідь, π².)

2.    Осьовим перерізом циліндра є квадрат зі стороною 8 см. Знайдіть бічну поверхню циліндра. (Відповідь. 64π см².)

3.    Радіус циліндра дорівнює r, а діагональ осьового перерізу — d. Знайдіть площу бічної поверхні і площу повної поверхні циліндра.

(Відповідь. 2πr; 2πr(r + ).) 

4.   Площа поверхні і площа бічної поверхні циліндра дорівнюють 50 см²  і 30 см². Знайдіть радіус і висоту циліндра. (Відповідь.  см; см.)

IV. Домашнє завдання

V. Підведення підсумку уроку

Запитання до класу

1)  Чому дорівнює площа бічної поверхні циліндра?

2)  Запишіть формулу для знаходження площі бічної та повної поверх­ні циліндра.

3)  Висота конуса дорівнює Н, а діагональ осьового перерізу утворює з площиною основи кут 45°. Укажіть, які з наведених тверджень правильні, а які — неправильні:

а) радіус циліндра дорівнює ;

б) площа основи циліндра дорівнює πН²;

в) бічна поверхня циліндра дорівнює ;

г) повна поверхня циліндра дорівнює .

Спостереження та висновки

• Щодо структури уроку: на етап вивчення нового матеріалу було відведено 15 хв., по факту знадобилось 20-25 хв. Учні досить довго не розуміли з чого почати роботу. Тому на розв’язування задач часу майже не було. Краще, якщо на цей урок буде приділятися 90 хв. Тоді можна доповнити урок більшою кількістю задач або іншими цікавими завданнями.
• Щодо роботи учнів з кейсом: такий кейс розвиває просторове мислення, бо необхідно переходити з тривимірних форм на двомірну розгортку.
• Робота учнів з уявною розгорткою: найбільшою проблемою виявилось обчислити площу кільця циліндра. Спочатку учні обчислили повну поверхню циліндра і на цьому вирішили, що робота закінчилась, доки однин з учнів не спитав: «А що роботи з кільцем?». Був зроблений висновок, що те розв’язання некоректне.
• В цілому, урок учням сподобався. Учні зробили висновок, що завдання було нескладним, але було зробили багато помилок, бо такі завдання вимагають від учнів не тільки знання формул, розвинутої просторової уяви, а й ще уважності й обчислюваних навичок. Щоб навчитися вирішувати такі завдання безпомилково, потрібна велика індивідуальна робота вчителя з кожним учнем, що забирає багато часу. Вважаю, що використання кейс-методу вирішить цю проблему. Роль вчителя виконують однокласники в групах, які допоможуть один одному знайти помилки, пояснити незрозумілі моменти. Оптимальне рішення не нав'язується учителем, а учні в результаті обговорення самі знаходять його. Воно стає їм більш зрозумілим, коротке рішення цих задач зводить до мінімуму обчислювальні і смислові помилки.