Урок по геометрии "Правильные многогранники" для 11 класа

Про матеріал

Розробка відкритого уроку з геометрії для 11 класу , що вивчають математику на рівні стандарту.

Перегляд файлу

УРОК НА ТЕМУ: «ПРАВИЛЬНЫЕ МНОГОГРАННИКИ»

Скоч Н.В., учитель математики

ООШ №9 г. Бердянска

Тема урока: Правильные многогранники.

Цель урока:

Учебная: формировать понятие правильного многогранника, рассмотреть каждый из пяти видов правильных многогранников, совершенствовать навыки решения задач.

Развивающая: развивать творческую активность учащихся, пространственное воображение, память, развивать логическое мышление, умение анализировать.

Воспитательная: воспитывать сознательное отношение к обучению, целеустремленность, трудолюбие, воспитывать культуру труда.

Тип урока: комбинированный.

Методы проведения урока: работа в группах, беседа, рассказ.

Межпредметные связи: Биология, история, химия, архитектура, художественная культура.

Оборудование: фотографии, модели правильных многогранников, раздаточный материал.

Литература:

А.Р. Гальперіна Математика (рівень стандарту). Тестовий контроль результатів навчання. 11 кл. : навч.посібник для загальноосвіт. навч. закл. – Х.: Літера ЛТД, 2019р.
Г. П. Бевз, В. Г. Бевз. Математика: 11 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту. - К.: Освіта, 2019р.
Т. Л. Корнієнко, В. І. Фіготіна. Математика. 11 клас. Академічний рівень: Розробки уроків. – Х: Видавництво «Ранок», 2014 р.
Интернет ресурсы: https://uk.wikipedia.org/wiki/
https://stroi.mos.ru/unikalnaya-arhitektura/mir/zdaniie-ghorod-dlia-novogho-orlieana
https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2016/03/25/mnogogranniki-v-nashey-zhizni
https://sites.google.com/site/vstranemnogogrannikov/metodiceskaa-kopilka/mnogogranniki-vokrug-nas

Эпиграф урока:

Правильных многогранников очень мало, но этот очень скромный по количеству отряд сумел пробиться в самые глубины различных наук.

Льюис Кэрролл

Ход урока

I. Организационный момент

Приветствие, проверка присутствия учеников, готовности их к уроку.

"От того настроения, с которым вы вступаете

в день, или в какое-то дело, зависят ваши

успехи, а возможно, и неудачи ".

Конфуций

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\confucius.jpg$

Поэтому я желаю вам начать урок с хорошим настроением и получить от него удовольствие и новые знания.

II. Актуализация опорных знаний учащихся

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\мольєр.jpg$

"Как приятно узнать, что ты чему-то научился" Мольер

Но перед тем как начать изучать новую тему предлагаю повторить темы «Многогранники» и «Призмы».

Для этого у вас на столах есть два варианта тестовых заданий и у вас есть 5 мин на ответы.

Самопроверка. За каждый правильный ответ 1 балл (из правильных ответов должно получиться слово ИКОСАЭДР)

III. Мотивация учебной деятельности

Геометрия представляет собой мощный инструмент познания мира.

Тема сегодняшнего урока "Правильные многогранники".

Существует всего 5 правильных многогранников. Название каждого правильного многогранника происходит от греческого названия количества его граней и слова "грань". Правильные многогранники имеют богатую историю, которая связана с таким знаменитыми учеными древности, как Пифагор, Платон, Эвклид, Архимед, Кеплер.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\піфагор.jpg$

Пифагор

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\платон.jpg$

Платон

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\Interesnie_fakti_o_Evklide_3.jpg$

Эвклид

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\archimedes.jpg$

Архимед

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\Johannes_Kepler_1610a.jpg$

Кеплер

В античной философии первоосновой бытия считали 4 стихии: огонь, земля, воздух и вода. Древнегреческий философ Платон придавал атомам этих "стихий" форму тетраэдра, куба, октаэдра и икосаэдра. Форму додекаэдра Платон придавал всей Вселенной.

Ни одно геометрическое тело не имеет такого совершенства и красоты, как правильные многогранники. Сегодня на уроке мы познакомимся с понятием правильных многогранников, их видами и элементами. Найдем правильные многогранники в природе, истории, архитектуре, искусстве.

IV. Восприятие и осознание нового учебного материала

Определение: Правильным называется выпуклый многогранник, у которого все грани - равные правильные многоугольники и в каждой вершине сходится одинаковое число ребер.

Поскольку существует пять видов правильных многогранников и каждый из них имеет определенное количество граней, вершин, ребер, то я вам раздала таблички, которые вы будете заполнять в течение объяснения.

Название	К-во граней (Г)	К-во вершин (В)	К-во ребер (Р)	К-во вершин и граней (Г + В)
Тетраэдр
Куб (гексаэдр)
Октаэдр
Икосаэдр
Додекаэдр

Виды правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

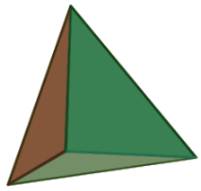
1. Правильный тетраэдр

Определение: Правильным тетраэдром называется многогранник, у которого все грани правильные треугольники и в каждой вершине сходится по 3 ребра.

Тетраэдр имеет следующие элементы:

Вершин – 4

Ребер – 6

Граней – 4

Высота тетраэдра - длина перпендикуляра опущенного из вершины на плоскость.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\220px-Tetrahedron.svg.png$

В физическом мире тетраэдр встречается в:

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\sneginka_mikroskop1.jpg$

ледяных кристаллах

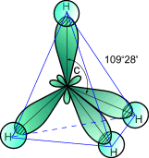
$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\молекула метану.png$

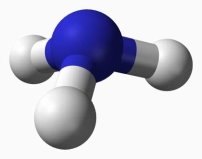
молекулах метана

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\аміак.jpg$

молекулах аммиака

Тетраэдр в архитектуре:

В Новом Орлеане разработан проэкт "Здание-город". Грандиозная пирамидальная конструкция способна выполнить роль «ноева ковчега» - плавучее здание сможет без потерь пережить любой шторм или прилив.

Здание будет складываться из плоской основы площадью около 3 млн «квадратов» и трех башен высотой порядка 366 метров, которые плавно сойдутся вверху.

Благодаря внутреннему пустому пространству пирамида свободно пропустит сквозь себя мощный ветер в любом направлении.

В основании предусмотрены тысячи ячеек для воздуха, которые смогут поддерживать пирамиду на плаву.

По задумке архитектора, «Здание-город» может стать настоящим городом в миниатюре и вместить 40 тысяч человек. Помимо 20 тысяч квартир, здесь расположатся три отеля, магазины и казино, школы и госпитали, культурные учреждения.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\будівля-місто.jpg$

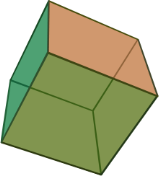
2. Куб или гексаэдр

Определение: Правильным гексаэдром называется многогранник, у которого все грани - квадраты и в каждой вершине сходится по 3 ребра.

Куб имеет следующие элементы:

Вершин – 8

Ребер – 12

Граней – 6

Высота гексаэдра - это длина ребра.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\220px-Hexahedron.svg.png$

Куб в архитектуре:

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\кубічна голова.JPG$

Архитектура в Ницце - "Кубическая Голова"

Вот что бывает от большого ума. Хотя, Голова полезная - поскольку в ней размещена администрация городской библиотеки.

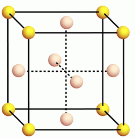
В физическом мире куб встречается в:

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\сіль.jpg$

кристаллах поваренной соли,

кристаллических решетках таких металлов:

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\кристалічна будова алюмінію.jpg$

алюминий,

золото, серебро, железо, цинк.

По образному выражению Пифагора "соль была рождена благородным родителями - солнцем и морем".

Украина имеет большие и уникальные по качеству залежи сырья для поваренной соли, по химической чистоте их можно считать лучшими в мире. Основные запасы: Прикарпатье, Донбасс, Закарпатье, а также в Крыму. Высококачественная каменная соль является важной составляющей экспорта Украины. Тысячелетия назад соль была настолько дорогой, что из-за нее устраивали войны. Сейчас соль является самой дешевой из всех видов пищевых добавок.

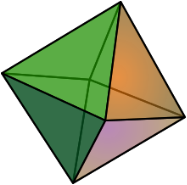
3. Октаэдр

Определение: Правильным октаэдром называется многогранник, у которого все грани - правильные треугольники и в каждой вершине сходится 4 ребра.

Октаэдр имеет следующие элементы:

Вершин – 6

Ребер – 12

Граней – 8

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\220px-Octahedron.svg.png$

В форме октаэдра кристаллизуются

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\мідь.jpg$

медь

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\алмаз.jpg$

алмаз

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\250px-SilverUSGOV.jpg$

серебро

Алмаз - это драгоценный кристалл и является самым твердым из веществ. В промышленности алмазы, благодаря их чрезвычайной твердости, используют для шлифовки, сверления и резки, бурения твердых горных пород, обработки твердых металлов и других сплавов и тому подобное.

Ограненные ювелирные алмазы называют бриллиантами. По последним исследованиям в Украине обнаружены два перспективных участки по нахождению алмазоносных кимберлитов, которые расположены в Донецкой и Ровенской области.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\діамант.jpg$

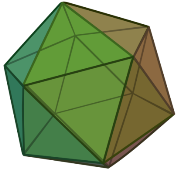
4. Икосаэдр

Определение: Правильным икосаэдром называется многогранник, у которого все грани - правильные треугольники и в каждой вершине сходится 5 ребер.

Икосаэдр имеет следующие элементы:

Вершин - 12

Ребер – 30

Граней – 20

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\1200px-Icosahedron.svg.png$

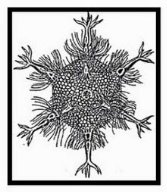
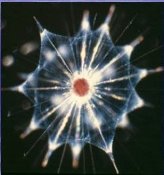
Скелет одноклеточного организма феодарии имеет форму икосаэдра. Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите.

Чем же вызвана такая природная геометризация феодарии? Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство позволяет морскому организму преодолевать давление воды.	$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\феодарія.jpg$		$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\феодарія 2.jpg$
	Феодарии

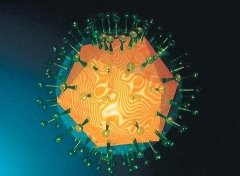
$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\gerpes03.jpg$ Вирус герпеса		Исключительностью икосаэдра воспользовались и вирусы. Вирус не может быть совершенно круглым, как считалось ранее. Вирус в форме икосаэдра достигает максимальной экономии генетической информации.

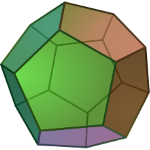
5. Додекаэдр

Определение: Правильным додекаэдром называется многогранник, у которого все грани - правильные пятиугольники и в каждой вершине сходится 3 ребра. Додекаэдр имеет следующие элементы:

Вершин – 20

Ребер – 30

Граней – 12

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\Dodecahedron.svg.png$

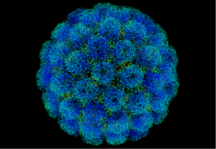
Некоторые из правильных тел встречаются в виде кристаллов, другие в виде вирусов, или простейших микроорганизмов.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\поліомієліт.png$

К примеру, вирус полиомиелита имеет форму додекаэдра. Он может жить и размножаться только в клетках человека и приматов. Заразиться полиомиелитом можно только от людей. Вирусы передаются через переносчиков (клещи).

Додекаэдр и икосаэдр являются параметрами ДНК, по которой построена вся жизнь.

Молекулы ДНК представляют собой куб, который вращается. При повороте куба на 72 градусов получается икосаэдр, который составляет пару додекаэдру.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\днк.jpg$ $C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\пірит.jpg$

Молекула ДНК Кристалл пирита - природная модель додекаэдра

На картине Сальвадора Дали "Тайная Вечеря", Иисус Христос и 12 учеников находятся в модернистском интерьере со стеклянными стенами. Апостолы, наклонив головы, стоят на коленях вокруг стола. Сальвадор Дали создал эту картину по математическим принципам. Чувствуется влияние Леонардо да Винчи: вселенная - это додекаэдр.

$C:\Users\TOSHIBA\Desktop\Бокало Ганна\Відкритий урок\таємна вечеря.jpg$

Сальвадор Дали “Тайная Вечеря”

V. Осмысление, обобщение и систематизация знаний

Название	К-во граней (Г)	К-во вершин (В)	К-во ребер (Р)	К-во вершин и граней (Г + В)
Тетраэдр	4	4	6	8
Куб(гексаэдр)	6	8	12	14
Октаэдр	8	6	12	14
Икосаэдр	20	12	30	32
Додекаэдр	12	20	30	32

Эвристическая беседа:

- Не замечаете ли вы какой-то закономерности?

- Запишем ее так: Г + В = Р + 2.

Так мы получили формулу, которая была открыта швейцарским математиком Леонардом Эйлером в 1752 году.

Это теорема о соотношении между числом граней, ребер и вершин для любого выпуклого многогранника.

Практическое задание:

Работа по группам. Построить модели правильных многогранников, имея их развертки и представить готовые модели.

Вопросы к ученикам:

- Какой многогранник называется правильным?

- Сколько существует видов правильных многогранников?

- Существует ли пирамида, которая является правильным многогранником?

- Существует призма, которая является правильным многогранником?

Решение задач:

У тетраэдра площадь одной грани 4 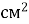. Найти площадь всего тетраэдра.
Сколько нужно провода, чтобы изготовить куб, ребро которого равно 20 см?
Найти периметр одной грани октаэдра, если его ребро равно 5 см?
Площадь одной грани гексаэдра равна 144 см². Найти диагональ этого многогранника.

VI. Итог урока

Правильные многогранники существовали на земле задолго до появления на ней человека. Но только математики увидели в них порядок и систему задолго до того, как физики проникли в тайну строения вещества.

Судя по этому правильные многогранники будут играть все более важную роль в различных областях знаний, ведь эти фигуры внутренне связаны с природными явлениями.

Как говорил Платон, из всех известных тел они самые прекрасные, причем каждый многогранник прекрасен по-своему. Пожалуй, это тот случай, когда красота и истина - единое целое.

VIІ. Домашнее задание

Г. П. Бевз, В. Г. Бевз. Математика: 11 кл.: підруч. для загальноосвіт. навч. закл.: рівень стандарту. - К.: Освіта, 2019р.

§ 19 ст. 166-169, № 702, 704, 709.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Скоч Наталія Володимирівна

Пов’язані теми

Математика, 11 клас, Розробки уроків

Додано

26 грудня 2019