Урок по темі "Вектори на площині"

Тема: «Вектори на площині»     9 клас

Тема уроку: Означення вектора. Модуль і напрям вектора. Коленіарні вектори. Рівні вектори.

Мета уроку: сформувати поняття вектора, коленіарних векторів, рівних векторів;

домогтися засвоєння властивостей і ознак рівних векторів;

сформувати вміння розв’язувати задачі, що передбачають застосування поняття вектора;

розвивати культуру математичного мовлення й записів;

виховувати інтерес до вивчення математики

Очікувані результати: учні повинні знати означення вектора, коленіарних векторів, рівних векторів, властивості й ознаки рівних векторів, уміти застосовувати ці знання до розв’язування задач.

Основні поняття: вектор, довжина вектора, нульовий вектор, коленіарні вектори, рівні вектори, властивості й ознаки рівних векторів

Обладнання: підручник (О.С.Істер Геометрія, 9 клас) , роздавальні матеріали, на екрані Евдокса Книдського

Тип уроку: засвоєння нових знань і вмінь

Хід уроку

1. Організаційний етап

Ознайомити учнів з планом вивчення теми «Вектори на площині», повідомити дату написання контрольної роботи з цієї теми, звернути увагу на тематику повідомлень і рефератів, які можна підготувати впродовж вивчення теми

2. Актуалізація опорних знань

Розв’язування задач.

Знайти довжину відрізка АВ, якщо А(2; 3), В(-1; 4).

Знайти середину відрізка АВ, якщо А(3; -2), В(-4; 6)

3. Формулювання теми, мети й завдань уроку; мотивація  навчальної діяльності

Слово вчителя

Напевно, вам відомо з курсу фізики, що деякі величини характеризуються не тільки числовим значенням, але й напрямом. Наведіть приклади таких величин. (Учні наводять приклади: швидкість, прискорення, сила тощо).

Необхідність математичного моделювання таких величин спричинила створення теорії векторів. Сьогодні ви дізнаєтесь, що називають вектором, які вектори називають коленіарними, рівними, а також навчитеся розв’язувати задачі на застосування поняття вектора.

Історична довідка на сторінці 57. (розповідь учня)

Цікавість до векторів з’явилась у математиків ХІХ ст. у зв’язку з розвитком механіки й фізики, проте витоки числення з напрямленими відрізками виникли в далекому минулому.

Математики часів Піфагора та математики більш пізніх часів намагалися зводити вирішення питань арифметики й алгебри до розв’язування задач геометричним шляхом. Таким чином було покладено початок геометричній теорії відношень Евдокса (408 – 355 р.р. до н.е.), а пізніше – геометричної алгебри.

Сам термін вектор (від латинського vector, що можна перекласти як «той, що веде», «той, що переносить») запропонував Гамільтон. Він же описав і деякі операції векторного аналізу. Незабаром, завдяки роботам Геббса (кінець ХІХ ст.) та Хевісайда (початок ХХ ст.), векторний аналіз, як частина математики, набув сучасного вигляду.

4. Сприйняття та усвідомлення нового матеріалу.

Фронтальна бесіда

План

1. Означення вектора
2. Довжина (модуль) вектора.
3. Означення нульового вектора.
4. Означення коленіарних векторів.
5. Означення співнапрямлених і протилежно напрямлених векторів.
6. Означення рівних векторів.

5. Осмислення нового матеріалу

1.     Робота в парах №271; №275.
2.     Виконання графічних вправ №273, №277, №283.
3.     Виконання усних вправ №288, №293.
4.     Перевірити свою компетентність №281.

6. Підбиття підсумків уроку

Бліц опитування  (запитання в підручнику стор. 57)

1. Які величини називають скалярними?
2. Які величини називають векторними?
3. Що називають вектором?
4. Яка точка є початком вектора 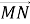, а яка – кінцем цього вектора?
5. Як позначають вектора?
6. Що називають модулем вектора ?
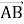7. Які вектори називають коленіарними?
8. Які вектори називають рівними?

7. Домашнє завдання §6, №278, №282, №276