Урок по темі: "Застосування розв’язування трикутників у задачах"
Тема: Застосування розв’язання трикутників у задачах
Мета: Сформувати вміння застосовувати алгоритми розв’язання трикутників до розв’язання задач; розвивати вміння логічно мислити, пам’ять, увагу; виховувати інтерес до вивчення математики
Очікувані результати: Учні повинні вміти розв’язувати трикутники
Обладнання: Підручник, роздавальні матеріали, реферат, слайди
Тип уроку: Застосування знань і вмінь
Епіграф до уроку:
«Знати – це означає, насамперед, уміти користуватися знаннями»
В.О. Сухомлинський
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Самоперевірка за готовими розв’язаннями
№595
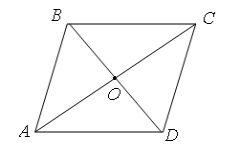
Дано: АВСD – паралелограм
АС і BD – діагоналі
АС = 10см, BD = 8см
![]()
Знайти: АВ, ВС, ![]() ,
, ![]()
Розв’язання
Оскільки ABCD – паралелограм, то
![]() ;
; ![]() (см)
(см)
![]() ;
; ![]() (см)
(см)
З ∆АОВ ![]()
![]()
![]() ;
;
![]() ;
;
![]() ;
; ![]() см
см
![]() суміжні з
суміжні з ![]() , тому
, тому
![]()
З ∆ВОС ![]()
![]()
![]()
![]() ;
; ![]() см
см
З ∆![]()
![]()
![]()
![]()
![]()
![]() , оскільки сума кутів паралелограма прилеглих до однієї сторони дорівнює
, оскільки сума кутів паралелограма прилеглих до однієї сторони дорівнює ![]()
![]()
Відповідь: 5,23см; 7,39см; ![]() ;
; ![]()
III. Формулювання теми, мети й завдання уроку; мотивація навчальної діяльності.
Слово вчителя:
Упродовж декількох останніх уроків ви вивчали теореми косинусів і синусів – основні «інструменти» для розв’язування трикутників.
Рубрика «Історична довідка»:
Навести історичну довідку про теорію косинусів та синусів (реферат учня)
Теорема косинусів відома ще стародавнім грекам. У твердженнях 12 і 13 другої книги «начал» Евкліда розглянуто питання про квадрати сторони трикутника, яка лежить проти гострого і проти тупого кута.
Безпосередньо для плоских трикутників теорему косинусів довів арабський астроном і математик Абу-я-Вафа (940-998). Дещо пізніше доводить і використовує цю теорему знаменитий середньоазіатський учений-енциклопедист Ал-Біруні (973-1048)
В Європа теорему косинусів по-справжньому оцінив і почав систематично використовувати знаменитий французький алгебраїст Француа Вієт (1540-1603)
Вважають, що теорему синусів вперше довів учитель Ал-Біруні іранський, математик Ібн-Ірак. Доведення цієї теореми зустрічається і в працях Ал-Біруні.
IV. Актуалізація опорних знать
Фронтальне опитування за технологією «мікрофон».
- Сформувати теорему косинусів;
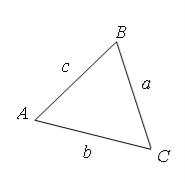
![]()
- Сформулювати теорему синусів;
![]()
-
Сформулювати теорему про суму кутів, кутів (
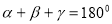 )
)
- Яку властивість для діагоналей паралелограма можна довести за допомогою теореми косинусів?
(Сума квадратів діагоналей паралелограма дорівнює сумі квадратів його сторін)
Ви розумієте, що існують практичні задачі, які можна розв’язати, знаючи як розв’язують трикутники. Сьогодні ви будете розв’язувати такі задачі, застосовуючи алгоритми розв’язування трикутників. Слайд 1, 2, 3, 4.
V. Застосування знань і вмінь
Перевір свою компетентність (робота в парах)
За даними наведеними на малюнках, знайти x
Перша пара Друга пара
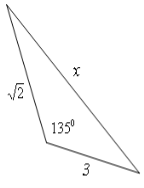
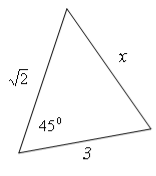
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Третя пара Четверта пара
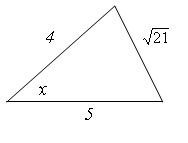
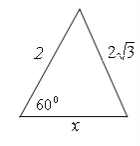
![]()
![]()
![]()
![]()
![]()
![]()
![]() - не задовольняє рівняння
- не задовольняє рівняння ![]()
![]()
![]()
Слово вчителя:
Як ви думаєте, чи можна, стоячи на одному березі річки, визначати висоту фабричного димаря. До основи якого не можна підійти? (Відповідь: так) Для цього потрібно мати нехитрі вимірювальні пристрої і вміти розв’язувати трикутники, тобто знаходити невідомі елементи трикутника за його відомими елементами.
Розв’язання практичних задач
Робота в групах
1. Визначити висоту фабричного димаря ВD до основи якого не можна підійти, виміряти довжину базису, відрізка АС, продовження якого перпендикулярне до висоти димаря. ![]() ,
, ![]() ,
, ![]()
Розв’язання
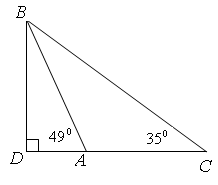
Із трикутника ABC:
![]()
Оскільки ![]() то
то ![]()
![]()
Тоді ![]()
![]() (м)
(м)
Із трикутника ![]() :
: ![]()
![]() (м)
(м)
Відповідь: ![]()
2. Під час військових дій на одній із ділянок фронту ситуація склалася так, що ворожий снайпер, який добре замаскувався постійно загрожував життю солдатів. Завдання полягає в тому, щоб виявити схованку снайпера та знищити його. Для цього необхідно було застосувати математичні розрахунки. Зроблено такі вимірювання:![]() ,
, ![]() ,
, ![]()
Слово вчителя:
Ваших знань цілком вистачить для того, щоб знайти схованку ворога.
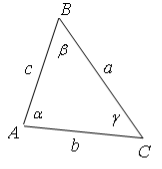
Розв’язання
Нехай ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() .
.
За теоремо синусів
![]()
![]() ;
; ![]() ;
;
Отримаємо: ![]() ;
; ![]()
Аналогічно: ![]() ;
; ![]() ;
; ![]()
Відповідь: ![]() ;
; ![]()
VI. Підсумки уроку
Бліц - опитування
VII. Домашнє завдання
§13 №590
О.С.Істер Геометрія
Підручник для 9 класу загальноосвітніх навчальних закладів


про публікацію авторської розробки
Додати розробку
