Тема.  Розв’язування задач практичного змісту

Мета: вчити застосовувати подібність трикутників у вирішенні конкретних практичних завдань; розвивати логічне мислення, інтуїцію, уміння встановлювати причинно-наслідкові зв’язки на між наочній основі; виховувати позитивне відношення до знань; показати значущість геометрії.

Тип уроку: застосування знань, формування навичок.

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Запитання

1. У трикутників АВС і DEF кути А і В рівні. Якої умови недостатньо для того, щоб стверджувати, що ці трикутники подібні за І ознакою?

2. Як можна розрізати прямою будь-який прямокутний трикутник на два подібних трикутника?

З метою економії часу перевіряються лише відповіді та коротко обговорюється план розв’язування задач домашнього завдання.

ІІІ. Формулювання мети і завдань уроку, мотивація навчальної діяльності

                            Геометрія — це мистецтво добре вимірювати.

П. Раме, ХVІст.

Історично склалося так, що математика виникла з практичних потреб людини на основі задач, поставлених життям, і розвивалась з їх розв’язанням. Історія геометрії зберігає немало прийомів вирішення завдань на знаходження відстаней. Дуже важливим і цікавим є перехід від тексту прикладної задачі до так званої «математичної моделі задач». Чим ми з вами і займемося на сьогоднішньому уроці.

ІV. Формування вмінь, навичок

№1. Знайдемо висоту дерева, якщо до нього можна підійти. Зріст людини  165см, відстань від людини до дерева 4,7м.

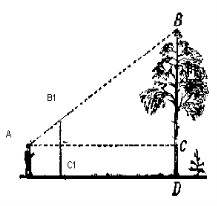Розв’язання.

     Для того, щоб виміряти висоту дерева ВD, треба виготовити прямокутний ∆АВ₁С₁ з А = 45°, С₁ = 90°. Тримаючи його вертикально, на рівні очей, підійти до дерева на таку відстань, при якій, дивлячись уздовж гіпотенузи АВ₁, побачити верхівку дерева В.

 Розглянемо   ∆АВС і ∆АВ₁С₁. В цих трикутниках А – спільний, С =С₁ = 90°. Тоді ∆АВС ~ ∆АВ₁С₁  за двома кутами.

  В   ∆АВ₁С₁    А = В₁ = 45°, то   ∆АВ₁С₁ – рівнобедрений, а значить і ∆АВС теж рівнобедрений. Звідси АС = ВС = 4,7см. Отже, ВD = ВС + СD = 4,7 + 1,65 = 6,35(м).

Відповідь: 6,35см.

№2.Знайти висоту дерева, якщо до нього підійти не можна. Зріст людини h.

Розв’язання.

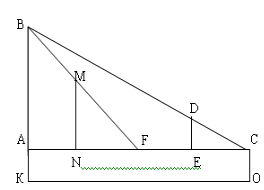(Спосіб лісорубів). Для того, щоб виміряти висоту  дерева  ВК, треба виготовити  два прямокутних трикутника. ∆DСЕ  з Е = 90°,  DE = х,  ЕС = 2х  і ∆МFN з N = 90°, МN = NF = ЕС = 2х. Аналогічно до задачі №1  доводиться    подібність  ∆МFN  ~ ∆ВFА і  ∆DСЕ ~ ∆ВСА.                                                                                                                                                                        Звідси  АF = АВ  і АС = 2АВ.                                                                                                        Тоді  FС  =  2АВ – АВ = АВ.                                                                         Отже, ВК = FС + АК = FС + h (FС – відстань  між  трикутника  яку можна виміряти на місцевості).                                                                                                                                                                                                  

     Відповідь: FС + h.                                                             

   №3.   Галасливий гурт хлопчиків зупинився на крутому березі річки. Прямо перед   ними шумів  могутній Дніпро. «Ось би перепливти!», – прошепотів Вадим. «Ти, що, нам  не здолати!»,  тут же парирував Женя.  Лише найрозумніший з компанії, відмінник Вітя, зітхнувши, тихенько прошепотів: « І чого тут сперечатися! Можна все прорахувати».  Хлопці  голосно розсміялися.

 – Ти що, попливеш?

      – І не подумаю. Дивіться.

Рівно через  5 хвилин задоволений Вітя поважно повідомив, що ширина річки  дорівнює ... метрів.

Продемонструйте варіант рішення, який придумав Вітя.       

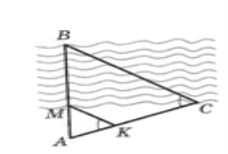Розв’язання.

      Довести подібність ∆АМК і ∆АВС можна  аналогічно  попереднім   задачам.   Відстані АК,  АС  і  АМ   можна  виміряти.  Із подібності   АК : АС = АМ : АВ.                                                                            Звідси АВ =  АМ ∙ АС : АК.  Відстань МВ =  АВ – АМ. Отже, АВ = АМ ∙ АС : АК –  АМ.

     Нехай АС = 100м, АК = 32м, АМ = 36м, тоді АВ = 76,5м.                                                                                                                                                              

 Відповідь: АВ = АМ ∙ АС : АК – АМ, АВ = 76,5м.

№4. З двох населених пунктів А і В одночасно назустріч один одному виходять два туристи. При зустрічі виявляється, що турист, що вийшов з пункту А, пройшов на 2 км. більше, ніж турист, що вийшов з пункту В. Продовжуючи рух з тією ж швидкістю, перший турист прибуває у В через 1 год 36 хв, а другий в А – через 2 год 30 хв. Знайдіть відстань АВ і швидкість кожного туриста.

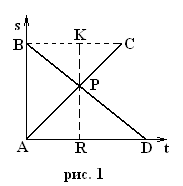                  Розв’язання.                                                         

 Побудуємо  графіки  руху   туристів.   За умовою  задачі  PR –  PK = 2; KC = 1,6; RD = 2,5.  Знайдемо AB. З подібності трикутників ( ∆BKP~ ~ ∆DRP,  ∆CKP ~  ∆ARP)  витікає, що КС : АR = = КР : РR =  ВК : RD. Але BK = AR, тому  AR² = = 1,6 ·  2,5,  AR = 2.  Далі 1,6 : 2 = РК : (РК + 2). Звідки РК = 8км, АВ = 18км, υ₁ = 5км/год, υ₂ =   = 4км/год.                  .                                                                       Відповідь: υ₁ = 5км/год, υ₂ = 4км/год.

VІІ. Підсумки уроку

На уроці були розглянуті найбільш актуальні завдання, пов’язані з геометричними вимірами на місцевості – визначення   висоти   предмету,  знаходження   відстані   до недоступних предметів. Він показав нам, що завдання можуть бути різними, але при вирішенні багатьох проблем математика необхідна.

VІІІ. Домашнє завдання

Повторити матеріал, що вивчався на попередніх уроках.

№1.Відкрита ділянка дороги знаходиться на смузі СВ завширшки 50м і ворожий пункт спостереження знаходиться на дзвіниці АК =     = 22м. Якої висоти слід зробити вертикальну перепону на відстані 500м від дзвіниці, щоб закрити дорогу від спостерігача супротивника.

№2.Знайти відстань від острова, що знаходиться на озері, до пункту на березі.