Урок "Розв'язування задач на ознаку подібності за двома кутами"
Тема. Розв’язування задач на ознаку подібності трикутників за двома кутами
Мета: виробляти практичні уміння і навички розв’язування задач на подібність навики застосування набутих знань; розвивати вміння долати труднощі, аналізувати, активність, увагу, творчі здібності школярів.
Тип уроку: застосування знань, умінь і навичок.
Хід уроку
І. Організаційний етап
ІІ. Перевірка домашнього завдання
Оскільки вправи домашньої роботи відтворювали ситуації, аналогічні до розглянутих на попередньому уроці, перевіряється лише виконання створення моделі та обчислень.
Запитання.
-
Якщо
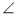 А =
А =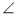 А1,
А1, 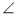 С =
С =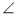 С1, то ∆АВС □ ∆А1В1С1. Тоді ВС : □ = = □ : А1В1 і
С1, то ∆АВС □ ∆А1В1С1. Тоді ВС : □ = = □ : А1В1 і  В = □.
В = □.
- Чи подібні два прямокутних трикутника, якщо один із них має кут 24°, а другий 66°? Відповідь поясніть.
- Чи подібні рівнобедрені трикутники, якщо вони мають по рівному гострому куту? Відповідь поясніть.
- З відрізків 4, 6, 8, 9, 12 і 18 склали два подібних між собою трикутника. Знайти коефіцієнт подібності цих трикутників.
ІІІ. Формулювання мети і завдань уроку
Розв’язання простої, але не зовсім стандартної може вимагати деякого напруження, зате натомість дає відчути тріумф відкриття.
За Д. Пойа
 ІV. Формування вмінь, навичок
ІV. Формування вмінь, навичок
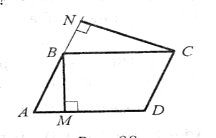
№1.У паралелограмі АВСD проведено висоти ВК і СМ (рис). Доведіть подібність трикутників АВК і СВМ.
№2.Гіпотенуза прямокутного трикутника дорівнює 20см, а більший катет – 16см. Знайдіть відрізки, на які серединний перпендикуляр гіпотенузи ділить більший катет.
 Розвязання.
Розвязання.
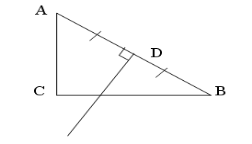
На рисунку в ∆АВС ![]() С = 90°, АВ = 20см, ВС = 16см, АD = DВ, DК
С = 90°, АВ = 20см, ВС = 16см, АD = DВ, DК ![]() АВ. Знайдемо АD і DВ.
АВ. Знайдемо АD і DВ.
Розглянемо ∆АВС і ∆КВD. В трикутниках ![]() С =
С = ![]() D = 90°,
D = 90°, ![]() В – спільний. Тоді ∆АВС ~ ∆КВD за двома кутами. Отже, АВ : КВ = ВС : DВ = АС : DК; 20 : КВ = 16 : 10; КВ = = 12,5см і СК = 3,5см.
В – спільний. Тоді ∆АВС ~ ∆КВD за двома кутами. Отже, АВ : КВ = ВС : DВ = АС : DК; 20 : КВ = 16 : 10; КВ = = 12,5см і СК = 3,5см.
 Відповідь: 12,5см і 3,5см.
Відповідь: 12,5см і 3,5см.
№3. У паралелограмі АВСD, через точку О – точку перетину діагоналей, проведено перпендикуляр КN до АD. АВ перетинається з КN в точці F. Знайти на які відрізки ділить перпендикуляр сторону ВС, якщо АВ = 2см, ВF = 5см, ВС = 9см.
№4. У рівнобедреному трикутнику АВ = ВС = 5см. На стороні ВС узята точка D так, щоб ВD = 1см. Відрізок АD перетинає висоту ВЕ в точці К. Знайдіть ![]() .
.
Розв’язання.
І спосіб ІІ спосіб
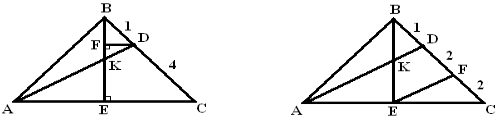
І спосіб. Опустимо перпендикуляр DF на ВЕ, тоді DF || СЕ. Розглянемо ∆ВСЕ і ∆ВDF. В трикутниках ![]() F =
F = ![]() Е = 90°,
Е = 90°, ![]() ВDF = = ВСЕ як відповідні. Тоді ∆ ВСЕ ~ ∆ ВDF за двома кутами. Звідси k = = ВС : ВD = СЕ : FD = 5.
ВDF = = ВСЕ як відповідні. Тоді ∆ ВСЕ ~ ∆ ВDF за двома кутами. Звідси k = = ВС : ВD = СЕ : FD = 5.
Розглянемо ∆ВСЕ і ∆ВDF. В трикутниках ![]() F =
F = ![]() Е = 90°,
Е = 90°, ![]() АКЕ =
АКЕ =
= ![]() DКF як вертикальні. Тоді ∆ВСЕ ~ ∆ ВDF за двома кутами. Тоді АЕ : FD = СЕ : FD = 5 (ВЕ за теоремою є медіаною і висотою). Звідси ЕК : КF = 5.
DКF як вертикальні. Тоді ∆ВСЕ ~ ∆ ВDF за двома кутами. Тоді АЕ : FD = СЕ : FD = 5 (ВЕ за теоремою є медіаною і висотою). Звідси ЕК : КF = 5.
Нехай КF = х, тоді ЕК = 5х, а FЕ = х + 5х = 6х.
Так як DF || СЕ, то за теоремою про пропорційні відрізки ВD : DС= = ВF : FЕ = ¼.
Нехай ВF = у, тоді FЕ = 4у. Отже, ВК : КЕ = (ВF + КF) : КЕ = = (у + х) : (5х). Так як FЕ = 4у = 6х, то у = 1,5х. Звідси ВК : КЕ = = (1,5х + х) : (5х) = ½.
ІІ спосіб. Проведемо ЕF—середню лінію ∆АDС. Звідки DF = FС = 2см. Так як за теоремою АD || ЕF, то і КD || ЕF. За теоремою про пропорційні відрізки ВD : DF = ВК : КЕ = ½.
Відповідь: ВК : КЕ = ½.
V. Підсумки уроку
 Який із рисунків зайвий. Чому?
Який із рисунків зайвий. Чому?
VІ. Домашнє завдання
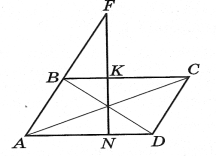
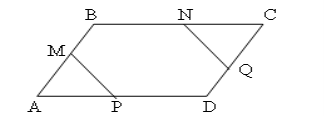 №1. АВСD – паралелограм, МР || NQ (рис.). Доведіть, що ∆АМР ~ ∆СQN.
№1. АВСD – паралелограм, МР || NQ (рис.). Доведіть, що ∆АМР ~ ∆СQN.
№2. Основа трикутника АВС дорівнює 5см, висота, проведена до цієї основи, дорівнює 3см. В трикутник вписаний квадрат так, що дві його вершини лежать на основі, а дві інші – на бічних сторонах. Обчисліть сторону квадрата.
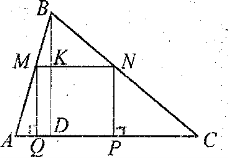 Розв’язання.
Розв’язання.
В ∆АВС основа АС = 5см, ВD = 3см – висота. МNPQ – квадрат, точка М є АВ, точка N є ВС, точки {Q, Р} є АС. Знайдемо МN. Розглянемо ∆АВС і ∆МВN. Оскільки МN ||АС, то ![]() А = М,
А = М, ![]() С =
С = ![]() N як відповідні. Тоді ∆АВС ~ ~ ∆МВN. Із подібності трикутників АВ : МВ = АС : МN = ВС : ВN = = ВD : ВК.
N як відповідні. Тоді ∆АВС ~ ~ ∆МВN. Із подібності трикутників АВ : МВ = АС : МN = ВС : ВN = = ВD : ВК.
Нехай МN = х см, тоді ВК = (3 – х) см, АС = 5см. Отже, 5 : х = = 3 : (3 – х); 5(3 – х) = 5х; х = 1⅞(см).
Відповідь: 1⅞ см.
1


про публікацію авторської розробки
Додати розробку
