Урок "Подібність трикутників" (8 клас, геометрія)

Відділ освіти, молоді та спорту

Новомиколаївської районної державної адміністрації

Запорізької області

 

 

 

 

 

Подібність трикутників

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

урок геометрії в 8 класі

проведений вчителем математики вищої кваліфікаційної категорії Підгірненської ЗОШ І-ІІІ ступенів

Бейдик Н. І.

 

 

Підгірне

Урок геометрії в 8 класі.

Тема уроку. Подібність трикутників.

Мета уроку:

• продовжити розвивати вміння аналізувати,класифікувати, порівнювати;
• розвивати логічне мислення, просторову уяву, увагу, пам’ять;
• виховувати розуміння ролі математики, важливості математичних знань;
• виховувати вміння сконцетруватися, слухати інших, співпереживати;
• сформувати уявлення про поняття подібних трикутників;
• сформувати вміння знаходити невідомі елементи подібних трикутників.

 

 

 

Тип уроку: комбінований.

Методи уроку: репродуктивний, практичний, індивідуально-диференційний.

Форми уроку: фронтально-колективна, індивідуальна.

Хід уроку

І. Організаційний момент

  

ІІ. Перевірка домашнього завдання; актуалізація опорних знань учнів

1. Сформувати узагальнену теорему Фалеса.
2. Сформулюйте наслідки з узагальненої теореми Фалеса.
3. 
   Сформулюйте властивість паралельних прямих.

III. Формулювання мети і задачі уроку.

Фалес Мілетський (VІ століття до н.е.)
Він мав титул одного із семи мудреців Греції, був першим філософом, першим математиком, астрономом; мав славу людини, що надала геометрії логіки, ввівши в неї доведення. Якщо раніше геометрів задовільняла відповідь на запитання «як», то Фалес ставив запитання «чому». «Фалес був для Греції тим, ким і Ломоносов для Росії.»

Як Фалес зміг виміряти висоту піраміди?

 

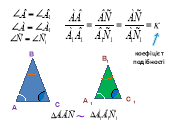
IV. Вивчення нового матеріалу.

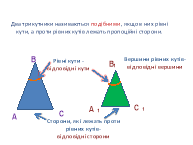
Два трикутники називаються подібними, якщо в них рівні кути, а проти рівних кутів лежать пропорційні сторони.

Рівні кути - відповідні кути

Вершини рівних кутів-відповідні вершини

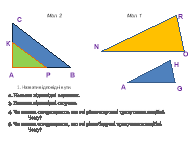
Сторони, які лежать проти рівних кутів-відповідні сторони

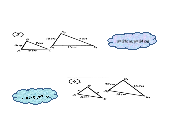
1. Назвати відповідні кути.

 2. Назвати відповідні вершини.

3. Назвати відповідні сторони.

4. Чи можна стверджувати, що всі рівносторонні трикутники подібні. Чому?

5. Чи можна стверджувати, що всі рівнобедрені трикутники подібні.  Чому?

 

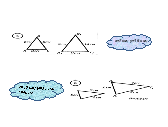
Задачі на закріплення вмінь і навичок учнів

 

Основна теорема подібності трикутників.

Паралельні прямі, які перетинають сторони трикутника, обмежують разом з його сторонами подібні трикутники.

Доведення.

1)

 

(як внутрішні різносторонні кути при паралельних прямих і січній)

2)

(за наслідком з узагальненої теореми Фалеса)

 

3)

(так  як паралелограм)

4)

Отже,

V. Закріплення і систематизація вивченого матеріалу.

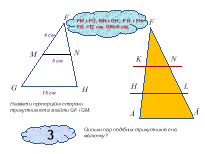
Назвати пропорційні сторони трикутників та знайти GF і GM.

Скільки пар подібних трикутників є на малюнку?

 

Виконати задачі (письмово, біля дошки).

 

 

 

 

 

 

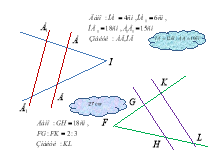
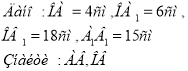
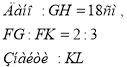
Як Фалес зміг виміряти висоту піраміди?

 

Самостійна робота (з елементами взаємоперевірки)

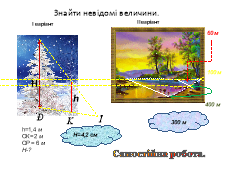
VI. Підсумок уроку. Домашнє завдання.

 

 

1. Які трикутники називаються подібними?

2. Що називається коефіцієнтом подібності?

3. Які елементи  у подібних трикутників залишаються незмінними?

4.Сформулюйте основну теорему подібності трикутників.

5. Де в нашому житті (в навколишньому середовищі) зустрічаються подібні трикутники?