урок"Похідна та її застосування"

Тема: Похідна та її застосування.

Мета: Формування предметних компетентностей:

• Систематизувати і поглибити теоретичні та практичні знання учнів.
• Орієнтувати учнів на знаходження і вивчення різноманітних зв’язків між математичними і фізичними  поняттями; ознайомити з історичним матеріалом, зв’язаним з поняттям «похідна».

Формування ключових компетентностей:

• Підвищити мотивацію учнів до опанування математики та фізики
• Створити атмосферу творчості.
• Формувати вміння працювати з джерелами додаткової інформації, аналізувати її, орієнтуватися у видозміненій ситуації.
• Розвивати вміння виступати перед аудиторією, коротко формулювати свою думку, аргументовано її доводити, розвивати логічне мислення, культуру математичного мовлення, інтерес до предмету, вміння працювати в команді.
• Виховувати уважність, активність, швидкість, самостійність учнів, наполегливість у досягненні мети.

 Тип уроку: інтегрований

Хід уроку

1. Вступне слово вчителя.
   Поняття похідної – одне з фундаментальних понять в математичному аналізі. Похідна використовується при розв’язуванні задач не тільки з математики, а й задач з фізики, хімії, економіки, будівництва. Знайомство учнів з метою уроку.
2. Актуалізація з опорних знань учнів.

1. Перевірка теоретичних знань учнів з заданої теми в процесі гри, яку проводить учениця класу. Гра проходить в 3 раунди. За кожну правильну відповідь учень одержує 1 бал. Кількість балів заноситься в залікову книжку, в якій оцінювання по трьом напрямкам: теоретичний матеріал, заповнення таблиць, розв’язування задач.

          Для проведення гри викликають 8 учнів.
          Питання:

I . раунд.

1. Сформулювати означення похідної в точці.
2. Який механічний зміст похідної?
3. Який геометричний зміст похідної?
4. Яка функція називається диференційованою в точці?
5. Яка функція називається диференційованою на інтервалі (а, в)?
6. В чому полягає механічний зміст похідної другого порядку?
7. Для розв’язування яких задач використовується поняття похідної?
8. Як дослідити функцію на екстремуми?

II .раунд.

1. Що таке коливання? Навести приклади.
2. При яких умовах виконуються коливання?
3. Які коливання називають гармонійними?
4. З чого складається коливальний рух?
5. Що ми називаємо математичним маятником?
6. Який маятник називається фізичним?
7. Назвіть формулу Гюйгенса для періоду коливань математичного маятника.
8. Назвіть формулу періоду коливань фізичного (пружного) маятника.

III . раунд.

1. Назвіть формулу Томсона для періоду коливань коливального контура.
2. Як знайти найбільше і найменше значення неперервної функції, заданої на відрізку?
3. Які коливання називаються вільними?
4. Яка точка називається екстремальною для функції у=f (х)?
5. Які коливання називають вимушеними? При яких умовах вони  виконуються?
6. Чи буде стаціонарна точка екстремальною для функції у=f (х)?
7. Які перетворення енергії відбуваються в коливальному контурі за період коливань?
8. В яких точках відрізка неперервна функція може набувати свого найбільшого і найменшого значень?

Два запитання для переможців.

1. Які коливання називаються затухаючими, на що витрачається енергія коливань?
2. Загальна схема дослідження функції і побудова графіка.
3. Заповнення таблиць. Потім взаємоперевірка

III . Розв’язування задач. Умови задач є на кожній парті:

а) Троє учнів розв’язують задачі біля дошки, а потім пояснюють

• Коливальний рух точки описується рівнянням x(t) = 0.05 cos20πt. Обчислити першу і другу похідну, записати  рівняння в залежності швидкості та прискорення від часу: v(t) і a(t). Знайти координату швидкості та прискорення через 60с  після  моменту t = 0.
• Заряд g на пластинах конденсатора коливального контуру змінюється з часом за законом g(t)= 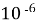cos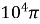t. Записати закон залежності сили струму від часу (I(t)). Знайти період часу, частоту коливань в контурі, амплітуду коливань заряду і амплітуду коливань сили струму.
• Написати рівняння дотичної до параболи x = 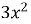-2  y точці x=-2

б) Із історії розвитку поняття похідної.
Розповідь підготували двоє учнів.

 в) Розв’язування творчих завдань біля дошки.

• Земельна ділянка прямокутної форми, розміщена вздовж прямого берега річки, її треба загородити з трьох сторін загорожею. Обчислити мінімальну вартість  загорожі, якщо погонний метр її обходиться в 10 грн, а площа земельної ділянки рівна 4,5 га.
• Сила струму визначається за законом Ома. Обчислити значення опору R, при якому потужність буде найбільша.

г)  Повторюємо основні алгоритми розв’язування задач.

д)  Самостійна робота (2 варіанта). Біля кожної задачі вказана кількість балів. Учень сам вибирає задачі, які він буде розв’язувати .

IV . Домашнє завдання: з алгебри повторити pVII, VIII, алгоритми розв’язування задач, підготуватися до контрольної роботи; з фізики: Р I, II.

V. Підведення підсумків уроку.

Самостійна робота

Варіант 1

1. Знайти найбільше і найменше значення функції : f (x) = 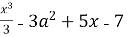на [ -1;3]. (3б.)
2. Знайдіть в якій точці графіка функції  f (x) = 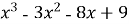 дотична нахилена до осі абсцис під кутом α =      (4б.)
3. Коливальний контур складається з конденсатора ємністю 1мкф і котушки індуктивністю 4 Гн. Амплітуда коливань заряду на конденсаторі 100 мкКл. Написати формули залежност g(t), i(t), u(t). Знайти амплітуди коливань сили струму і напруги (5 б.)

Варіант 2

1. Знайти найбільше і найменше значення функції : f (x) = на [ 2;4]. (3б.)
2. Знайдіть в якій точці графіка функції  f (x) = 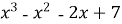дотична нахилена до осі абсцис під кутом α = 3π/4     (4б.)
3. Амплітуда коливань кінця ніжки камертона 1мм, а частота коливань 500 Гц. Написати рівняння x(t), v(t), a(t). Які найбільші значення швидкості і прискорення? В яких положеннях досягаються ці значення? (5 б)