Урок "Поняття площі. Властивості площі. Площа прямокутника та квадрата"

Геометрія                                                                                 Дата____________________

Урок №____

Тема. Поняття площі. Властивості площі. Площа прямокутника та квадрата.

Мета: увести поняття: площа простої фігури, площа многокутника,  плоский многокутник, властивості площі; формувати вміння знаходити площу прямокутника й квадрата, поновивши раніше отримані знання;

розвивати вміння порівнювати, робити висновки, узагальнювати;

виховувати культуру математичних записів, культуру математичного мовлення, інтерес до вивчення математики;

коригувати пам'ять, мислення, увагу.

Тип: засвоєння нових знань, умінь і навичок.

Хід уроку

1. Організаційний етап

Нервово-психологічна підготовка до уроку.

Корекція поведінки учнів.

2. Перевірка домашнього завдання

3. Формулювання мети та завдань уроку

Нагадуємо учням, що їм вже відоме поняття "площа" і вони вміють обчислювати площі деяких фігур, наводить ряд прикладів, пов'язаних із практичною необхідністю виміру площ: площа поверхні стін, підлоги — для розрахунку кількості фарби, шпалер, кахлі, клею; площі поверхні доріг — для розрахунку кількості асфальту і т. ін. Учні згадують відомі їм формули обчислення площ прямокутника й квадрата.

4. Актуалізація опорних знань і опитування учнів

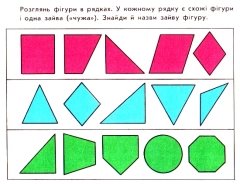
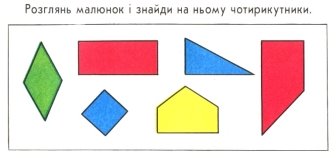
5. Вивчення нового матеріалу

Многокутником називається кінцева частина площини, обмежена многокутником (рис. 1).

Для простих фігур площа — додатна величина, чисельне значення якої має такі властивості:

1. Рівні фігури мають рівні площі.

2. Якщо фігура розбивається на частини, які є простими фігурами,

то площа фігури дорівнює сумі площ її частин (рис. 2, 3).

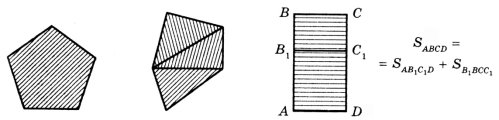
                               рис. 1                   рис. 2                   рис. 3

Площа квадрата зі стороною, рівною одиниці виміру, дорівнює квадратній одиниці (рис. 4).

Площа прямокутника зі сторонами а і b обчислюється за форму­лою S = аb (рис. 5).

рис. 4                                          рис. 5

Питання класу: чому дорівнює площа квадрата зі стороною а?

6. Первинне закріплення нових знань учнів

Розв’язування задач за готовими малюнками.

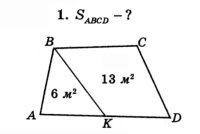
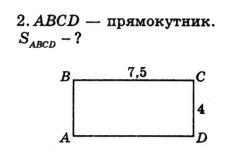
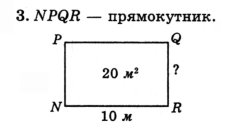
Виконання усних вправ

1.    Знайдіть площу прямокутника, сторони якого дорівнюють

      ¼ см і 1,6 дм.

2.    Знайдіть площу квадрата, сторона якого дорівнює:

       а) 12 см;   б) 0,5 см;  в) т см.

3.    Знайдіть сторону квадрата, якщо його площа дорівнює:

       1) 196 см 2) т см².

4.    Одна із сторін прямокутника дорівнює 12 см, а його площа 120 см².

        Знайдіть другу сторону прямокутника.

Виконання письмових вправ

1.    Знайдіть сторони прямокутника, якщо вони відносяться як 4:7, а площа прямокутника дорівнює 112 см². (Відповідь: 8 см, 14 см.)

2.    Сторони двох квадратів дорівнюють 8 см і 16 см. Знайдіть сторону квадрата, площа якого дорівнює сумі площ цих квадратів. (Відповідь: 8см.)                                          

3.    Площа прямокутника дорівнює 21 см². Знайдіть сторони прям кутника, якщо одна з них на 4 см більша від другої. (Відповів З см, 7 см.)

4.    Квадрат і прямокутник мають рівні площі. Сторона квадрата дорівнює 8 см, а одна із сторін прямокутника 16 см. Знайдіть другу сторону прямокутника. (Відповідь: 4 см.)

5.    Довжина кімнати 5,4 см, а ширина — 4,2 см. Кімната має дм вікна завширшки 1,2 м і заввишки 1,6 м. Освітленість кімнати вважається нормальною, якщо площа вікон становить 20 % від площі підлоги. Чи нормально освітлена кімната? (Відповідь: ні.)

6.    Чому дорівнюють сторони прямокутника, якщо його периметр           

74 дм, а площа 3 м²? (Відповідь: 12 дм, 25 дм.)

7. Підсумки уроку

Питання та завдання класу

1.    Що нового ви довідалися на уроці?

2.    Що повторили сьогодні?

3.    Як зміниться площа квадрата, якщо його сторону:

      а) збільшити у 7 разів;  б) зменшити у 4 рази;  в) збільшити в п разів?

4.    Як зміниться площа прямокутника, якщо:

       а) одну з його сторін збільшити в 5 разів; 

       б) одну з його сторін зменшити в 3 рази;

       в) обидві сторони збільшити в 7 разів;

       г) одну сторону збільшити в 4 рази, а другу — у 6 разів;

       д) одну сторону збільшити в 8 разів другу зменшити в 2 рази?

5. Чи є вірними твердження:

     якщо фігури мають однакові площі, то вони ріні?

6. Чи можуть квадрати, які мають рівні площі, бути нерівними?

8. Домашнє завдання

1.    Практична робота. Виріжте з паперу два рівних прямокутних трикутники та складіть із них:

а) рівнобедрений трикут­ник;

б) прямокутник;

в) паралелограм, що не є прямокутником.

Поясніть, чому площі всіх, отриманих фігур рівні.

Середній рівень

2.    Сторони прямокутника дорівнюють 0,6 см і 4,9 см. Знайдіть його площу.

Достатній рівень

3.    Знайдіть сторону квадрата, якщо його площа дорівнює  6,25 см².

4.    Площа квадрата чисельно дорівнює його периметру. Знайдіть сторону квадрата.

5.    Площа прямокутника дорівнює 144 см². Знайдіть його сто­рони, якщо одна з них у 8 разів більша, ніж друга.

Високий рівень

6.    Площа квадрата в 2 рази більша від площі прямокутника. Сторона квадрата дорівнює 6 см, а одна зі сторін прямокутни­ка — 9 см. Знайдіть другу сторону прямокутника.

7.    Площа прямокутника дорівнює 48 см². Знайдіть його сторони, якщо їх півсума дорівнює 7 см.

8.    Повторіть означення та властивості паралелограма.