Урок "Повторення Числа та вирази." (алгебра 11)
1. 2 кг сплаву міді з оловом містить 40% міді. Скільки потрібно додати до цього сплаву олова, щоб отриманий сплав містив 16% міді?
 б) 2 кг
б) 2 кг
г) 4 кг
б) 0,5
 |
г) -1
б) 24
г) 4
б) 6
г) 8
Спростіть вираз:
![]()

1 б)
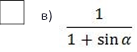
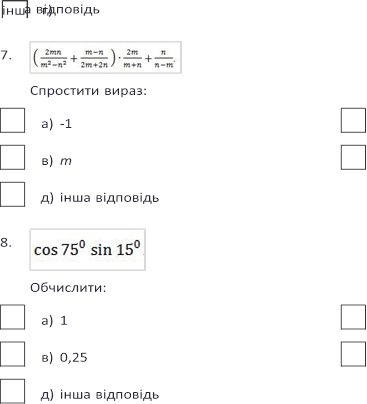
б) 1
г) n
б) 0,5
г) 0,75
Ключ до тесту
|
1. в (2 балів) |
2. в (1 балів) |
3. б (1 балів) |
4. б (2 балів) |
|
5. в (1 балів) |
6. б (2 балів) |
7. б (2 балів) |
8. в (1 балів) |
Тема уроку: Повторення: Числа та вирази.
Мета уроку:
-
систематизувати й узагальнити знання учнів про перетворення виразів різних типів, формувати вміння учнів виконувати перетворення алгебраїчних, тригонометричних, логарифмічних виразів, проводити відсоткові розрахунки;
- розвивати логічне мислення, самостійність, уміння зосередитися,
- формувати вміння швидко й чітко формулювати власні думки, логічно викладати й відстоювати їх;
- виховувати почуття відповідальності, віру у свої можливості й здібності;
- виховувати уміння сконцентруватися, слухати інших, співпереживати;
- формувати вміння співпрацювати в ході спільної навчальної діяльності.
Тип уроку: узагальнення, систематизація та застосування знань, умінь, навичок.
Форма організації уроку: колективна, групова, індивідуальна.
Хід уроку
І. Організаційний етап.
ІІ. Мотивація навчальної діяльності. Повідомлення теми і мети уроку.

Як досягти успіху? Це питання постає перед нами практично щодня. І як доречно буде вам винести зі школи не тільки багаж теоретичних знань та практичних умінь, а й деякі рецепти досягнення успіху.
Успіх легко виміряти. Це відстань між тим, з чого ви почали і вашим останнім досягненням.
Особливо важливо це для нас зараз - бо ми ведемо підготовку до ЗНО з математики. Тому я пропоную вам не тільки перевірити свої знання з алгебри, а й відповісти на запитання: що саме допоможе вам досягти успіху при складанні ЗНО?
Ми повернемося до цього запитання наприкінці уроку.
Ну а для досягнення успіху на уроці сьогодні вам знадобляться:
У – увага, усмішка, уява
С – сміливість
П – позитив
І - інноваційність, ініціативність
Х – хоробрість, харизматичність
І досягати успіху ми будемо у перетвореннях різних виразів.
ІІІ. Актуалізація опорних знань. «Шпаргалка».
До проведення уроку клас був поділений на групи, кожна група отримала наперед завдання – тему для підготовки опорного конспекту. Головною умовою створення «шпаргалки» було стисле, змістовне та небагатослівне викладення матеріалу.
На презентацію своєї «шпаргалки» відводиться в цілому 3 хв. Доповідач від групи коротко звітує про роботу, акцентує увагу на основних (на його думку) формулах або властивостях, а також пропонує решті учнів розв’язати одне усне завдання зі своєї теми.
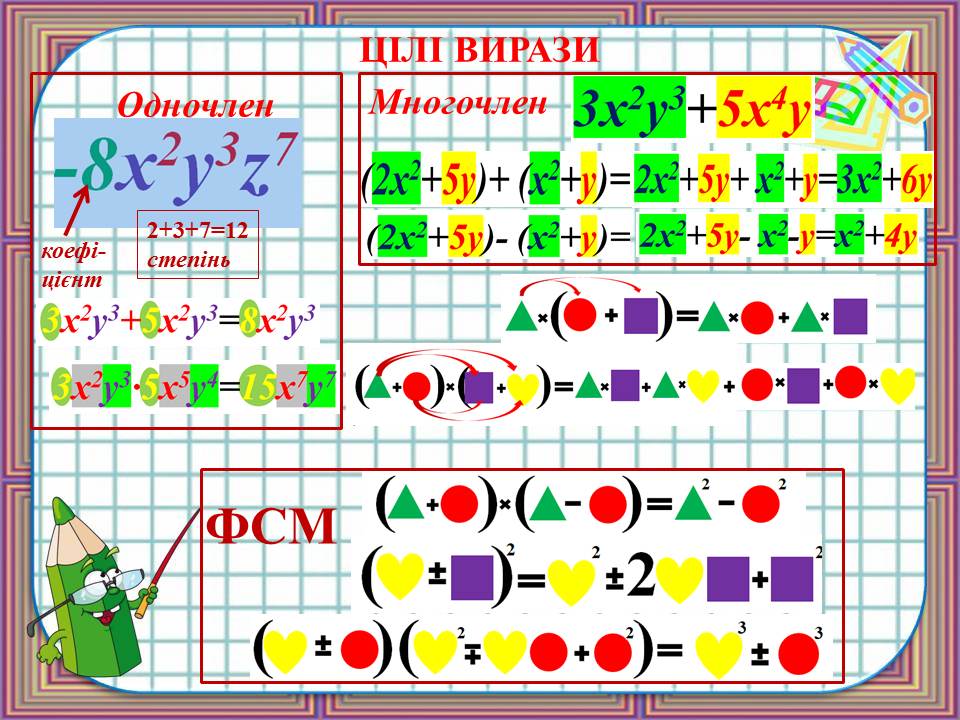
І група учнів готувала «шпаргалку» з теми «Цілі вирази».
Запропоноване завдання: Обчисліть усно 395∙405.
(395∙405=(400-5)(400+5)=1600-25=1575)
ІІ група учнів готувала «шпаргалку» з теми «Дробові вирази».
Запропоноване завдання: Розв’яжіть рівняння: ![]() .
.
(розв’язків немає; враховуємо ОДЗ ![]() )
)
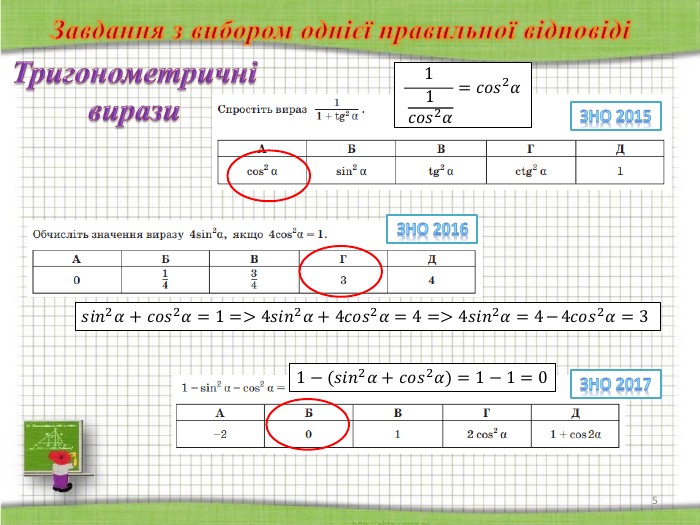
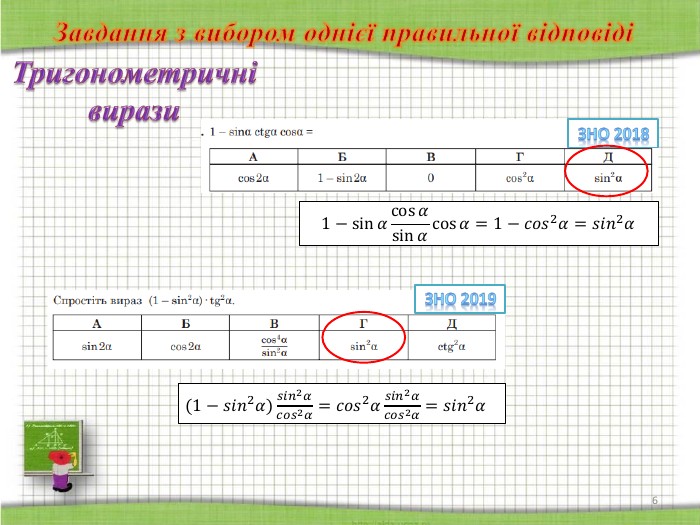
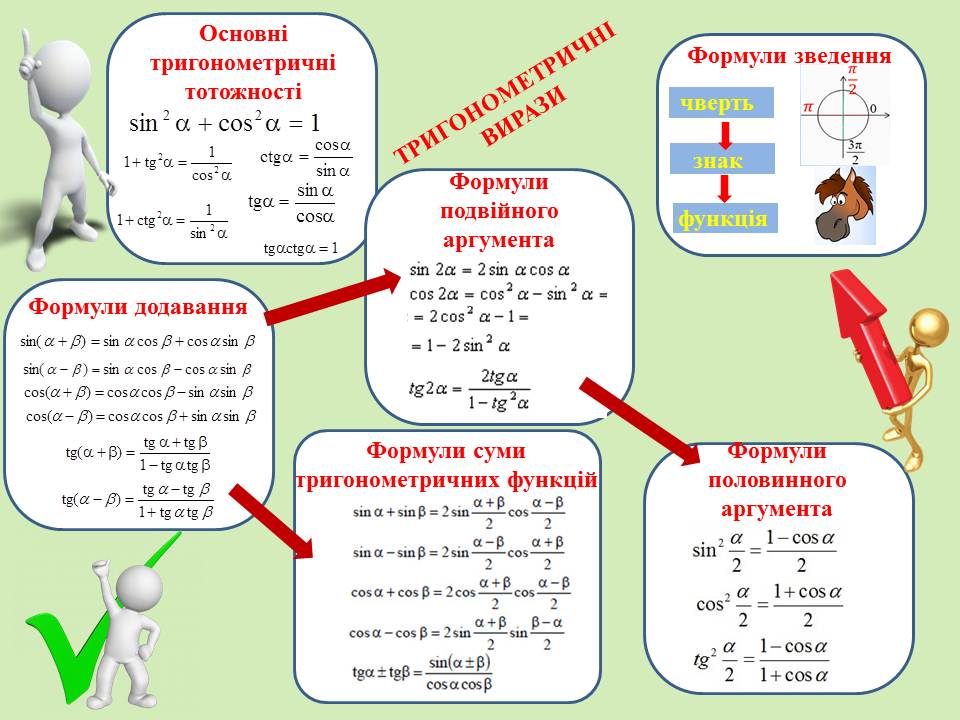
ІІІ група учнів готувала «шпаргалку» з теми «Тригонометричні вирази».
Запропоноване завдання: Обчисліть: ![]() .
.
(![]() ) =
) =![]()
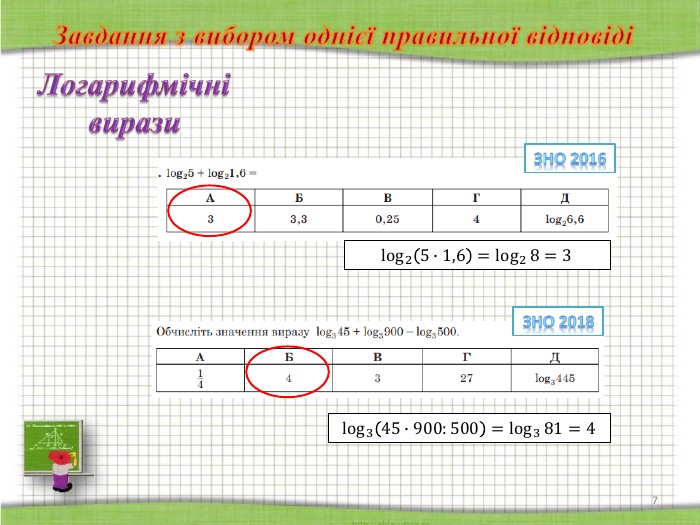
ІV група учнів готувала «шпаргалку» з теми «Логарифмічні вирази».
Запропоноване завдання: Обчисліть: ![]() .
.
(![]() )
)
V група учнів готувала «шпаргалку» з теми «Відсотки».
Запропоноване завдання: Ціну деякого товару спочатку підвищили на 10%, а потім знизили на 10 %. Як змiнилась цiна внаслiдок цих двох переоцiнок?
(знизилась; після підвищення стала 1,1х, після зниження 0,99х)
ІV. Застосування знань та вмінь.
Отже, ми з вами повторили теоретичні відомості з теми. А тепер настав час перевірити і відшліфувати свої вміння.
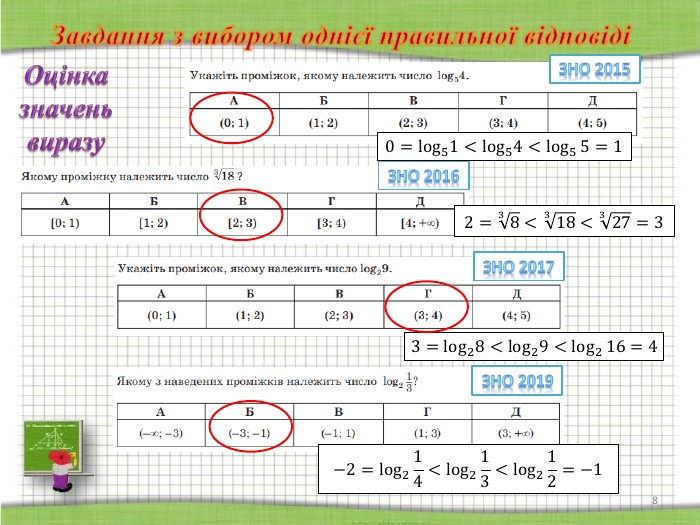
До вашої уваги пропоную завдання з теми «Числа та вирази», що пропонувалися у сертифікаційних роботах з математики протягом останніх років.
(демонструється підготована вчителем презентація, у якій зібрані завдання з даної теми у порядку, що відповідає структурі сертифікаційної роботи з математики )
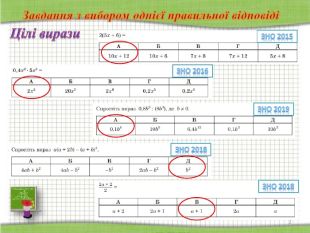
СЛАЙДИ 2-8
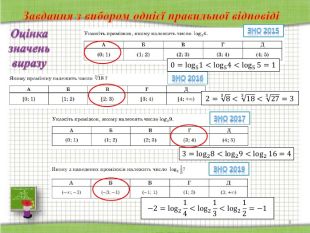
Завдання з вибором однієї правильної відповіді. Завдання має основу та п’ять варіантів відповіді, з яких лише один правильний. Завдання вважають виконаним, якщо учасник зовнішнього незалежного оцінювання вибрав і позначив відповідь у бланку відповідей А.
(учні працюють в групах; на столах мають сигнальні картки (А,Б,В,Г,Д) для відповідей; відповідь надається після кожного завдання; за потреби розв’язання обговорюються і записуються у зошитах)
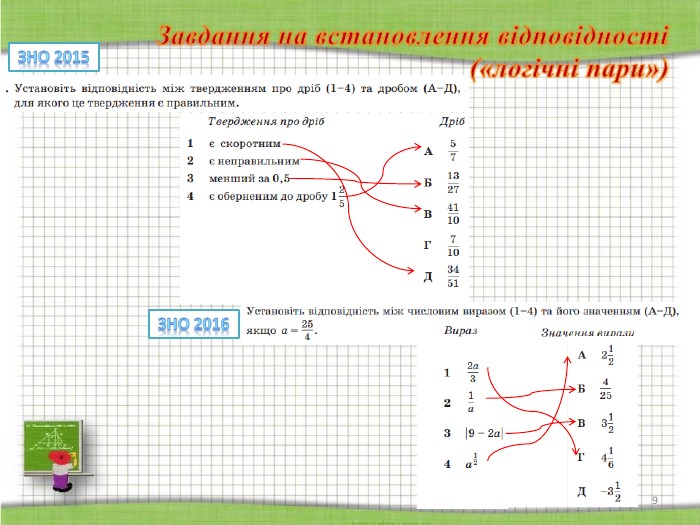
СЛАЙДИ 9-11
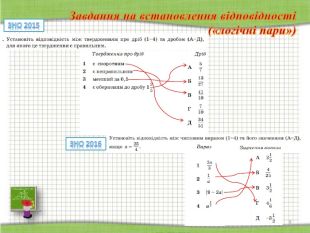
Завдання на встановлення відповідності («логічні пари»). Завдання має основу та два стовпчики інформації, позначених цифрами (ліворуч) і буквами (праворуч). Виконання завдання передбачає встановлення відповідності (утворення «логічних пар») між інформацією, позначеною цифрами та буквами. Завдання вважають виконаним, якщо учасник зовнішнього незалежного оцінювання зробив позначки на перетинах рядків (цифри від 1 до 3) і колонок (букви від А до Д) у таблиці бланка відповідей А.
(учні працюють в групах; надається час для виконання кожного завдання у зошитах, після чого звіряються відповіді; при необхідності складні і спірні моменти обговорюються )
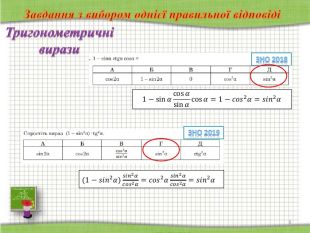
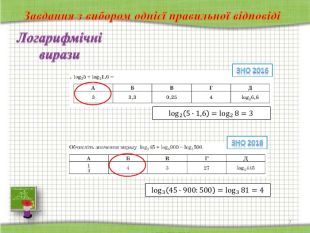
СЛАЙДИ 12-16
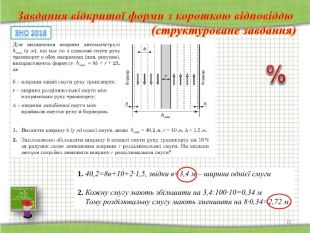
Завдання відкритої форми з короткою відповіддю (структуроване завдання): має основу та дві частини й передбачає розв’язування задачі. Завдання вважають виконаним, якщо учасник зовнішнього незалежного оцінювання, здійснивши відповідні числові розрахунки, записав, дотримуючись вимог і правил, відповіді до кожної з частин завдання в бланку відповідей А.
(кожна група отримує одне завдання ( група 1 – завдання зі слайду 12, ІІ – зі слайду 13 і т.д.); на його розв’язання відводиться час; після чого на дошці представниками груп записується відповідь; потім проглядаються слайди презентації; при необхідності складні і спірні моменти обговорюються)
СЛАЙД 17
Завдання відкритої форми з короткою відповіддю (неструктуроване завдання) має основу та передбачає розв’язування задачі. Завдання вважають виконаним, якщо учасник зовнішнього незалежного оцінювання, здійснивши відповідні числові розрахунки, записав, дотримуючись вимог і правил, кінцеву відповідь у бланку відповідей А.
(учні працюють в групах; надається час для виконання кожного завдання у зошитах, після чого звіряються відповіді; за потреби розв’язання обговорюються)
V. Підсумки уроку.
Метод: «Своя система оцінювання». Учні оцінюють свою роботу на уроці не загальноприйнятими балами, а за своєю шкалою, враховуючи свої очікування від уроку.
ДД – дуже добре
Д – добре
ЗК – знає, але не каже
КЗ – каже, але не знає
ГНК – гірше нема куди
Український філософ і письменник Г.С. Сковорода писав: «Найкраща помилка та, яку допускають під час навчання». Ці виявленні помилки допоможуть вам звернути увагу на матеріал, який виявився для вас складним, або вивчений недостатньо. Адже в сучасному житті показником успіху є не тільки кінцевий результат, а й процес його досягнення.
Зараз ми повертаємося до початку уроку до мети, яку ми з вами ставили перед собою. Так що саме допоможе вам досягти успіху при складанні ЗНО?
(відповіді учнів)
Перед вами на столах знаходяться рецепти з досягнення успіху на ЗНО. Ознайомтесь з ними.
Почніть із легких завдань! Почніть відповідати на ті запитання, в яких ви не сумніваєтеся, не зупиняйтеся на тих, які можуть викликати довгі роздуми.
Пропускайте! Треба навчитися пропускати складні або незрозумілі завдання. Просто безглуздо недобрати балів лише тому, що ви застрягли на тих завданнях, які викликають ускладнення.
Читайте завдання до кінця! Не прагніть зрозуміти умови завдання «за першими словами» і добудувати кінцівку у власній уяві. Це певний спосіб припуститися прикрих помилок у найлегших запитаннях.
Думайте лише про поточне завдання! Коли ви бачите нове завдання, забудьте все, що було в попередньому. Думайте лише про те, що кожне нове завдання — це шанс набрати бали.
Виключайте! Багато завдань можна швидше, вирішити, якщо не шукати одразу правильний варіант відповіді, а послідовно виключати ті, які явно не підходять.
Перевірте! Залиште час для перевірки своєї роботи, принаймні, аби встигнути переглянути і помітити явні помилки.
Вгадуйте! Якщо ви не впевнені у виборі відповіді, але інтуїтивно можете віддати перевагу якійсь одній, то інтуїції слід довіряти!
Не засмучуйтеся! Прагніть виконати всі завдання, але пам'ятайте, що на практиці це нереально. Враховуйте, що тестові завдання розраховані на максимальний рівень складності, і кількість вирішених вами завдань може виявитися цілком достатньою для гарної оцінки.
VІ. Домашнє завдання.
Відкривши посилання join.naurok.ua та використавши код доступу 693713 пройти домашній тест «Числа та вирази», записавши розв’язання завдань у зошит.
Поставтесь з відповідальністю до виконання домашнього завдання, оскільки з виконанням кожного завдання ви наближаєтесь до досягнення мети - успішної здачі ЗНО.
Дякую вам за урок! Хочу наприкінці уроку навести вислів великого Леонардо да Вінчі: «Якщо запастися терпінням і виявити старання, то посіяні насіння знання неодмінно дадуть добрі сходи». Що ми і перевіримо завтра на тестовій перевірочній роботі.
Домашній тест. Числа і вирази.
1. 2 кг сплаву міді з оловом містить 40% міді. Скільки потрібно додати до цього сплаву олова, щоб отриманий сплав містив 16% міді?
|
А |
Б |
В |
Г |
Д |
|
1 кг |
2 кг |
3 кг |
4 кг |
інша відповідь |
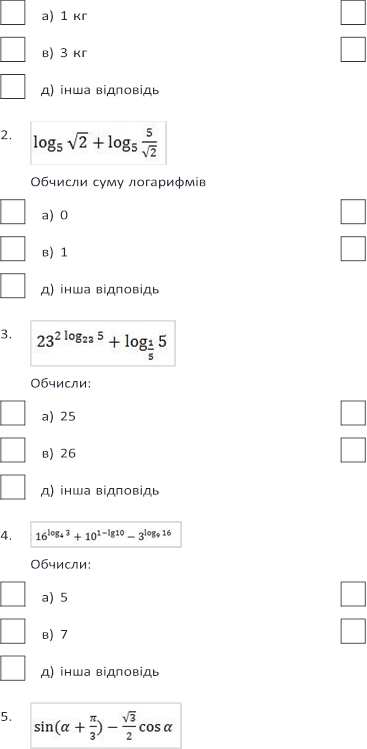
2. Обчислити суму логарифмів ![]()
|
А |
Б |
В |
Г |
Д |
|
0 |
0,5 |
1 |
-1 |
інша відповідь |
3. Обчисли: ![]()
|
А |
Б |
В |
Г |
Д |
|
25 |
24 |
26 |
4 |
інша відповідь |
4. Обчисли: ![]()
|
А |
Б |
В |
Г |
Д |
|
5 |
6 |
7 |
8 |
інша відповідь |
5. Спростіть вираз ![]()
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
інша відповідь |
6. Спростіть вираз: ![]()
|
А |
Б |
В |
Г |
Д |
|
|
1 |
|
0 |
інша відповідь |
7. Спростити вираз: ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
1 |
-1 |
m |
n |
інша відповідь |
8. Обчисли : ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
1 |
0,5 |
0,25 |
0,75 |
інша відповідь |
1


про публікацію авторської розробки
Додати розробку