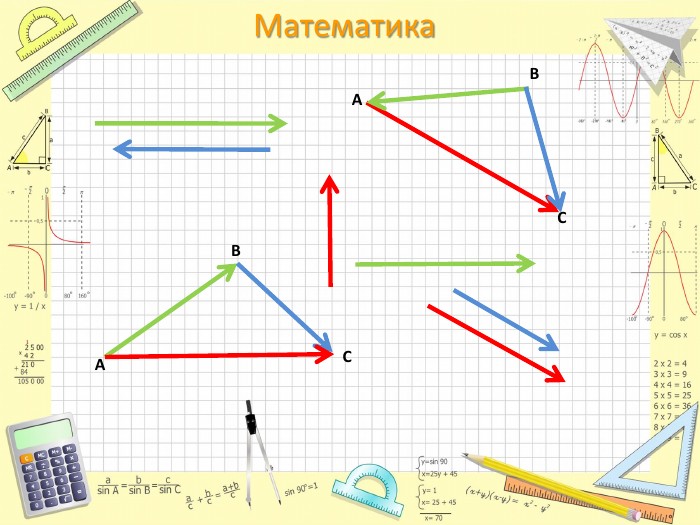
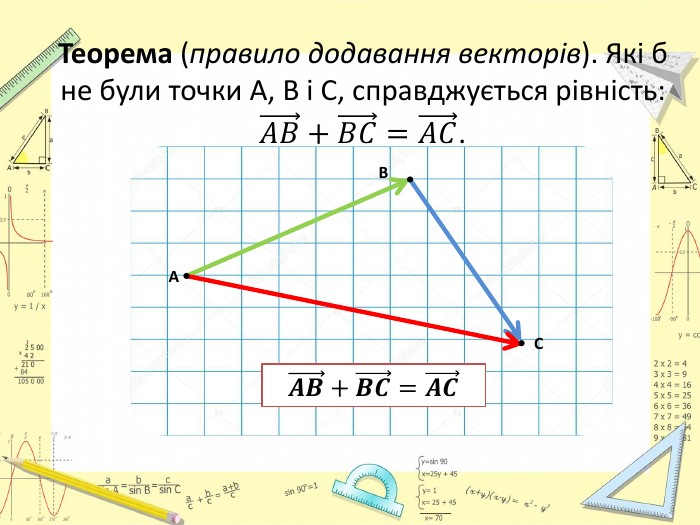
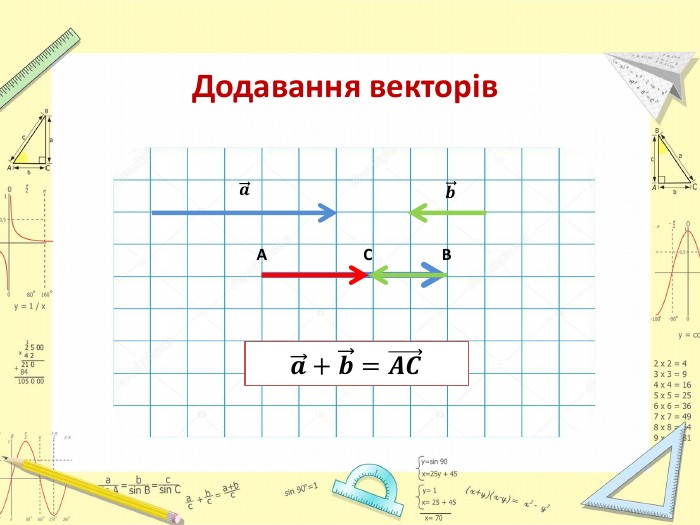
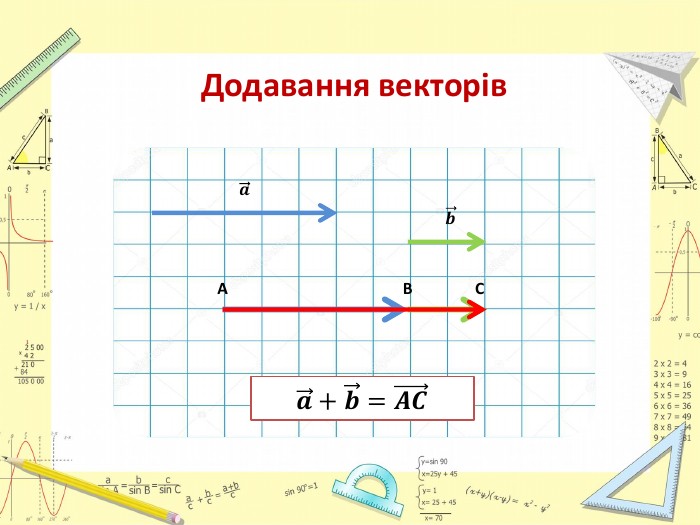
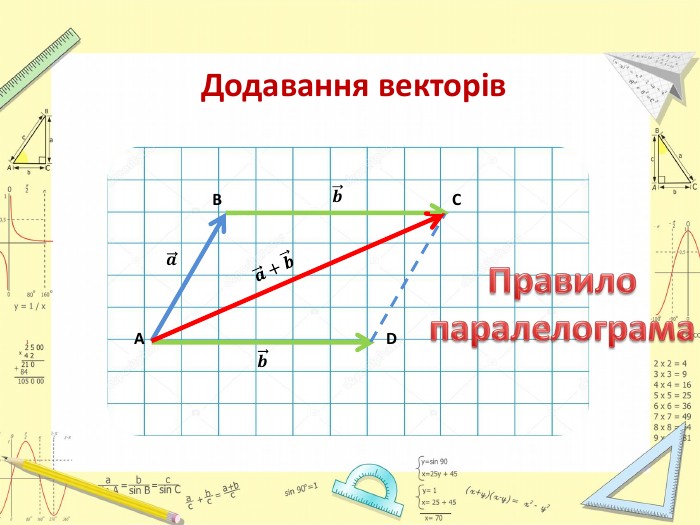
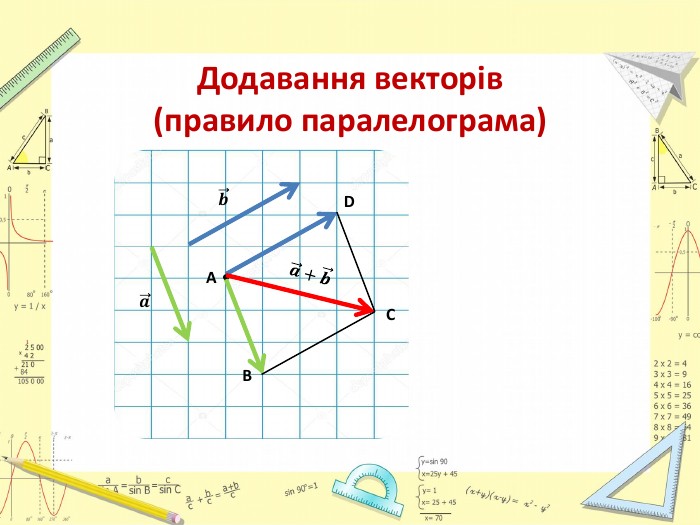
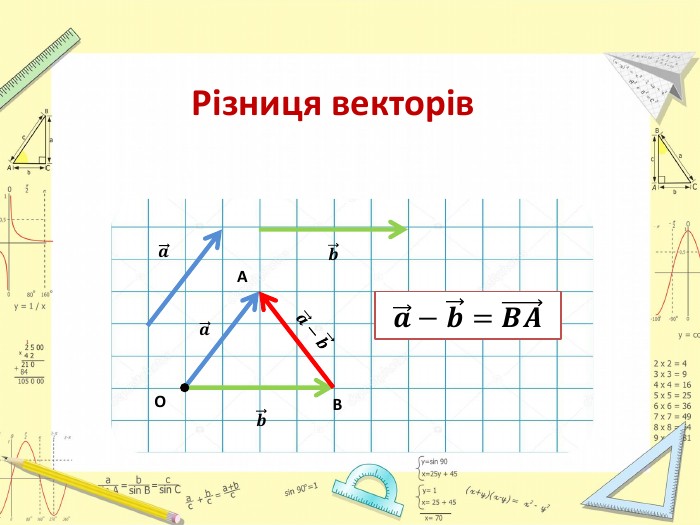
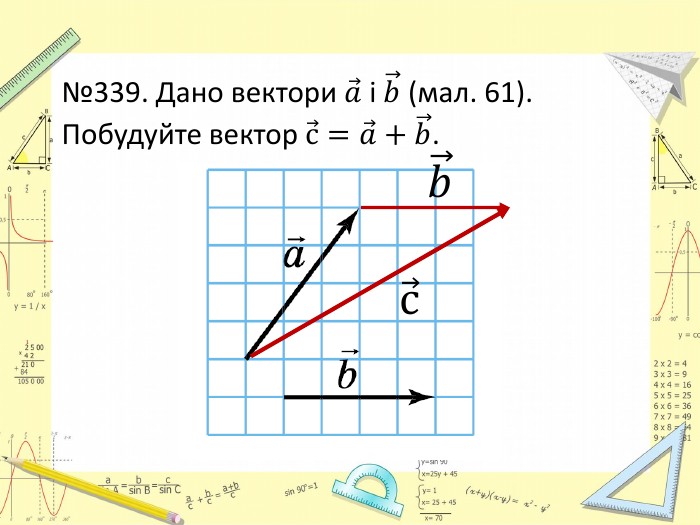
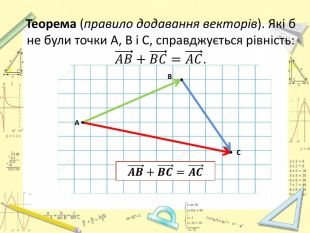
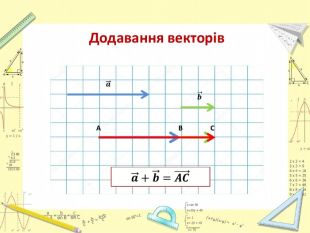
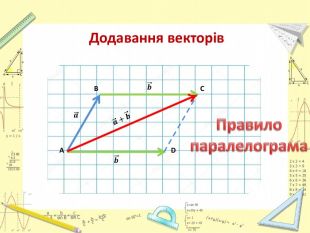
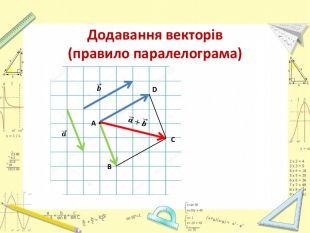
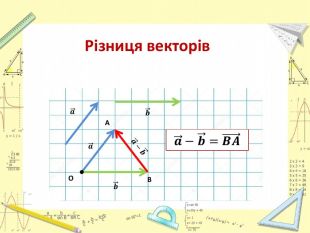
Презентація "Додавання і віднімання векторів"
Про матеріал
Презентація розроблена за підручником О. Істера (2017 р.) для учнів 9-х класів загальноосвітніх навчальних закладів. Містить матеріал для актуалізації знань, теоретичний матеріал, приклади, розв'язки задач Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Геометрія 9 клас (Істер О. С.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку