Урок-практикум (2 год) . Розв’язання типових задач. Самостійна робота.

Навчальний модуль

Об’єми та площі поверхонь

геометричних тіл

Геометрія 11 клас

  Підготувала вчитель математики

Яблунського ліцею

Солотвинської селищної ради

 Костур Дарія Дмитрівна

Конспект №5

Урок-практикум (2 год)

Тема модуля.  Розв’язання типових задач. Самостійна робота.

Мета модуля:  Удосконалити вміння розв’язувати задачі на обчислення площ поверхонь та об’ємів тіл обертання; провести огляд типових задач із цієї теми; перевірити рівень засвоєння знань з цієї теми шляхом проведення самостійної роботи; сприяти розвитку уваги, пам’яті учнів; виховувати інтерес до математики, наполегливість у роботі.

Тип модуля:  Адаптивно-перетворюючий.

Вид модуля: Урок типових задач.

Обладнання:  Картки із завданнями, кросворд, мультимедійний проектор, міні-підручники, екран, малюнки до усних вправ.

Хід уроку

Перший міні-модуль

І. Організаційний момент:

1. черговий збирає зошити з домашнім завданням і видає змінні;
2. учитель аналізує перевірені домашні роботи (в розданих зошитах);
3. робота над помилками, допущеними в перевіреній домашній роботі.

ІІ. Повідомлення плану уроку.

1. Розв’язування кросворда.
2. Розв’язування задач на знаходження площ поверхонь та об’ємів тіл обертання.
3. Проведення гри «Циліндр» – «Конус» – «Куля».
4. Самостійна робота.

Другий міні-модуль

ІІІ. Актуалізація опорних знань учнів.

Актуалізація опорних знань здійснюється у вигляді розгадування кросворда, який проектується на дошку за допомогою проектора і роздрукованого на окремих аркушах. Один учень на відкидній дошці, а всі інші на своїх аркушах, виконують завдання. Далі – взаємоперевірка.

Кросворд

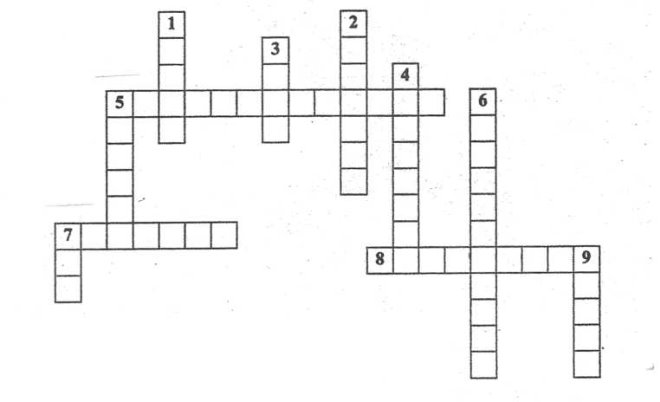
По вертикалі

1. Фігура, площа поверхні якої обчислюється за формулою .        2. Тіло, об’єм якого обчислюється за формулою . 3. Тіло, об’єм якого обчислюється за формулою . 4. Многогранник, об’єм якого обчислюється за формулою . 5. Многогранник, повна поверхня якого обчислюється за формулою . 6. Чотирикутник, площа якого обчислюється за формулою . 7. Тіло, об’єм якого обчислюється за формулою . 9. Тіло, об’єм якого обчислюється за формулою .

По горизонталі

5. Тіло, об’єм якого обчислюється за формулою .                            7. Чотирикутник, площа якого обчислюється за формулою . 8. Фігура, площа якої обчислюється за формулою .

Відповіді

По вертикалі. 1. Сфера. 2. Циліндр. 3. Куля. 4. Тетраедр. 5. Призма.                           6. Прямокутник. 7. Куб. 9. Конус.

По горизонталі. 5. Паралелепіпед. 7. Квадрат. 8. Трикутник.

Третій міні-модуль

IV. Розв’язування задач на знаходження площ поверхонь та об’ємів тіл обертання.

1.   Задачі за готовими малюнками.

Задача 1. В осьовому перерізі конуса R – радіус конуса, Н – висота, l – твірна, α – кут нахилу твірної до площини основи, β – кут між твірною та висотою.

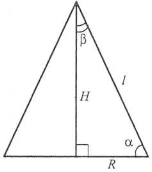
а) За відомими R та α знайти площу бічної поверхні.

б) За відомими R та α знайти об’єм конуса.

в) За відомими l та Н знайти об’єм конуса.

г) За відомими l та β знайти площу бічної поверхні.

д) За відомими l та β знайти об’єм конуса.

Задача 2. На зображенні розгортки бічної поверхні циліндра d – діагональ цієї розгортки, Н – висота циліндра, С – довжина кола основи, α – кут між діагоналлю розгортки та висотою циліндра.

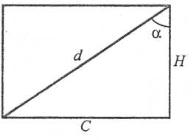
а) За відомими С та Н знайти об’єм циліндра.

б) За відомими d та α знайти об’єм циліндра.

Задача 3. Як зміниться об’єм циліндра, якщо:

а) Висоту і радіус збільшити у 3 рази?

(Збільшиться у 27 раз)

б) Висоту збільшити, а радіус зменшити у 3 рази?

(Зменшиться у 3 рази)

Задача 4. Діагоналі осьового перерізу циліндра взаємно перпендикулярні. Периметр перерізу дорівнює 8а. Знайти площу бічної поверхні.

2.   Тестові задачі.

1) Об’єми двох циліндрів відносяться як 27:64. Яке відношення їх радіусів?

А. 9:16.   Б. 27:64.   В.* 3:4.

2) У скільки разів збільшиться поверхня кулі, якщо її радіус збільшити у 3 рази?

А. У 6 раз.   Б.* У 9 раз.   В. У 3 рази.

3) Знайти об’єм кулі з радіусом 3 см.

А. 27π см³.   Б. 18π см³.   В.* 36π см³.

4) У циліндра та конуса однакові висота і радіус. Яка фігура має більший об’єм?

А.* Циліндр.  Б. Конус.   В. Об’єми рівні.

5) Формула об’єму кульового сегмента.

А. .  Б. .  В.* .

6) Що позначають буквою R у формулі об’єму кульового сектора ?

А.* Радіус кулі.  Б. Висоту сегмента.

В. Радіус кульового сегмента.

7) Виразити радіус конуса через площу бічної поверхні і твірну.

А. .   Б.* .   В. .

8) Чим є осьовий переріз конуса?

А. Прямокутним трикутником.

Б.* Рівнобедреним трикутником.

В. Різностороннім трикутником.

9) Твірна конуса – 5 см, висота – 4 см. Знайти його об’єм.

А.* 12π см³.  Б. 16π см³.   В. 36π см³.

10) Осьовий переріз циліндра – квадрат зі стороною 6 см. Знайти його об’єм.

А. 216π см³.  Б. 96π см³.   В.* 54π см³.

11) Як зміниться об’єм конуса, якщо його висоту збільшити у 2 рази, а радіус зменшити у 2 рази?

А. Збільшиться у 2 рази.

Б. Не зміниться.

В.* Зменшиться у 2 рази.

12) Твірна конуса 6 см, кут при вершині осьового перерізу 60^о. Знайти об’єм конуса.

А. см³.   Б.* см³.  В. см³.

3.   Текстові задачі.

Задача 1. Знайти об’єм тіла, яке утворюється обертанням трикутника АВС навколо осі, що проходить через вершину А і паралельна стороні ВС, якщо ВС=а, проекція ВА на вісь обертання дорівнює d і кут між АВ та віссю обертання дорівнює α.

Розв’язання

Тіло обертання є циліндром, з якого вилучено два конуси.

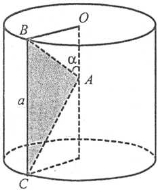
Його об’єм:

,

де , .

З трикутника :

.

Тоді .

Відповідь. .

Задача 2. Радіус кругового сектора АОВ дорівнює r, дуга АОВ дорівнює α. Сектор обертається навколо радіуса ОА. Знайти об’єм тіла обертання.

Розв’язання

Тіло обертання є кульовим сектором.

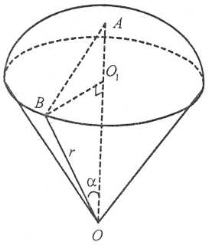
Його об’єм знайдено за формулою

,

де – радіус кулі,

З трикутника :

.

Тоді .

Отже, .

Відповідь. .

Четвертий міні-модуль

V. Гра «Циліндр» – «Конус» – «Куля»

Клас поділено на три команди «Циліндр», «Конус» і «Куля». Кожна команда ставить кілька запитань про свою фігуру командам суперників. Запитання задаються представником команд почергово, передбачаються усні відповіді.

П’ятий міні-модуль

VІ. Самостійна робота

Варіант 1.

Початковий та середній рівні навчальних досягнень

1.   З поміж наведених виберіть формулу для обчислення об’єму циліндра, якщо R і H – радіус і висота циліндра.

А) ;

Б) ;

В) ;

Г) .

2.   Радіус і висота конуса відповідно дорівнюють 2 см і см. Чому дорівнює об’єм конуса?

А) 2 см³;

Б) 3π см³;

В) 4 см³;

Г) 4π см³.

3.   Діаметр кулі дорівнює 6 см. Чому дорівнює об’єм кулі?

А) 432π см³;

Б) 36π см³;

В) 72π см³;

Г) 216π см³.

4.   Обчисліть площу повної поверхні циліндра, висота якого дорівнює 4 см, а площа основи – 9π см².

А) 21 см²;

Б) 42 см²;

В) 21π см²;

Г) 42π см².

5.   Висота конуса дорівнює 4 см, а радіус основи – 3 см. Обчисліть площу бічної поверхні конуса.

А) 8 см²;

Б) 15 см²;

В) 8π см²;

Г) 15π см².

6.   Діаметр сфери дорівнює 10 см. Чому дорівнює площа сфери?

А) 100 см²;

Б) 100π см²;

В) 25π см²;

Г) 20π см².

Достатній та високий рівні навчальних досягнень

1.   Радіус основи циліндра дорівнює 4 см. Знайдіть об’єм циліндра, якщо площа його осьового перерізу дорівнює 40 см².
2.   Радіус основи конуса дорівнює R, а його осьовий переріз – прямокутний трикутник. Знайдіть об’єм конуса.
3.   Площа перерізу кулі площиною, віддаленою від її центра на 15 см, дорівнює 64π см². Знайдіть об’єм кулі.
4.   Діагональ осьового перерізу циліндра дорівнює 18 см і нахилена до площини основи під кутом 60^о. Знайдіть площу бічної поверхні циліндра.
5.   Осьовим перерізом конуса є правильний трикутник, площа якого дорівнює 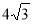см². Обчисліть площу бічної поверхні конуса.
6.   Площа великого круга кулі дорівнює 81π см². Знайдіть площу поверхні кулі.

Варіант 2.

Початковий та середній рівні навчальних досягнень

1.   З поміж наведених виберіть формулу для обчислення об’єму конуса, якщо R і H – радіус і висота конуса.

А) ;

Б) ;

В) ;

Г) .

2.   Радіус і висота циліндра відповідно дорівнюють 2 см і см. Чому дорівнює об’єм циліндра?

А) 18 см³;

Б) 12 см³;

В) 6 см³;

Г) 4 см³.

3.   Об’єм кулі дорівнює 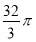см³. Чому дорівнює діаметр кулі?

А) 1 см;

Б) 2 см;

В) 4 см;

Г) 8 см.

4.   Обчисліть площу повної поверхні циліндра, висота якого дорівнює      6 см, а площа основи – 25π см².

А) 110 см²;

Б) 132 см²;

В) 110π см²;

Г) 132π см².

5.   Радіус основи конуса дорівнює 2 см, а висота – 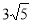см. Обчисліть площу бічної поверхні конуса.

А) 9 см²;

Б) 14π см²;

В) 9π см²;

Г) 14 см².

6.   Діаметр кулі дорівнює 8 см. Чому дорівнює площа поверхні сфери?

А) 16π см²;

Б) 32 см²;

В) 32π см²;

Г) 64π см².

Достатній та високий рівні навчальних досягнень

1.   Висота циліндра дорівнює 8 см. Знайдіть об’єм циліндра, якщо площа його осьового перерізу 32 см².
2.   Радіус основи конуса дорівнює R, а його осьовий переріз – рівносторонній трикутник. Знайдіть об’єм конуса.
3.   Довжина лінії перетину поверхні кулі і площини, віддаленої від її центра на 12 см, дорівнює 10π см. Знайдіть об’єм кулі.
4.   Осьовим перерізом циліндра є квадрат, діагональ якого дорівнює 8 см. Знайдіть площу бічної поверхні циліндра.
5.   Осьовим перерізом конуса є правильний трикутник, площа якого дорівнює 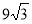см². Обчисліть площу бічної поверхні конуса.
6.   Площа великого круга кулі дорівнює 144π см². Обчисліть площу поверхні кулі.

VІІ. Підсумок практичного заняття

VІІІ. Домашнє завдання

1. Повторити §§7, 8 з підручника [5].
2. Підготуватися до захисту проектів.

Література

1. Пєхота О.М. Сучасні освітні технології. – К., А.С.К., 2001.
2. Смишляєва В.К. У світі математики. – К.; Рад. шк., 1976. – Випуск   7. – с. 183.
3. Пометун О., Пироженко Л. Сучасний урок. – К.: А.С.К., 2003.
4. Істер О.С., Глобін І.Є., Панкратова І.Є. Збірник завдань для державної підсумкової атестації з математики. – Київ.: ЦНМЛ, 2011.
5. Погорєлов О.В. Геометрія: Стереометрія: Підруч. Для 10-11 кл. серед. шк. К.: Освіта, 1998.
6. Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М. Геометрія: Стереометрія: Підруч. Для 11 кл загальноосвітніх навчальних закладів. – К.: «Генеза», 2011.
7. Погорєлов О.В. Геометрія: Планіметрія: Підручник для 7-9 кл. загальноосвітніх навчальних закладів. – К.: Школяр, 2004.