Урок "Побудова правильних многокутників"

Урок №3.

Тема уроку: Побудова правильних многокутників

Мета уроку: Ознайомлення учнів з правилами побудови правильних многокутників (трикутників, чотирикутників, шестикутників)

Тип уроку: комбінований

Обладнання:  підручник, презентація PowerPoint   

Хід уроку

І.  Організаційний момент

ІІ. Перевірка домашнього завдання    (Слайди 3-4)

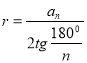
Завдання 9

б)n=3; r=2. Знайти а₃.                                                  

 

 

 

 

 

 

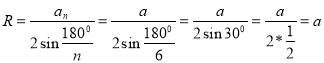Завдання 10

в) n=6;            . Знайти R

 

 

 

Завдання

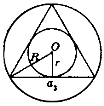
               Дано: правильний трикутник.

              

               Довести, що

 

Розв’язання:

 

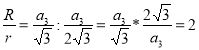
Так як                                ,     то  

 

Що й треба було довести.

 

ІІ. Актуалізація опорних знань  (Слайди 6-12)

 

1. Які багатокутники називаються правильними?

(Многокутники у яких всі сторони і всі кути рівні називається правильними)

2.Який багатокутник називається описаним навколо кола?

(Багатокутник називається  описаним навколо кола, якщо всі його сторони дотикається до кола)

3. Який багатокутник називається вписаним у коло?

(Багатокутник називається   вписаним у кола,  якщо всі його вершини лежать   на колі кола)

4.Допвніть речення:

Для правильного багатокутника центри вписаного і описаного кіл …

(збігаються)

5. Формулу радіусів вписаних і описаних кіл правильних многокутників

                     ;                              

 

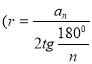
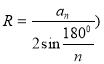Математичний диктант         (Слайди 13-14)

 

Дано коло радіус якого дорівнює 6 см.

 

Знайдіть:

1. Сторону правильного трикутника, вписаного в це коло.
2. Сторону правильного трикутника, описаного навколо кола.
3. Сторону правильного чотирикутника, описаного навколо даного кола.
4. Сторону правильного чотирикутника, вписаного в дане коло.
5. Сторону правильного шестикутника, вписаного в дане коло.
6. Периметр правильного шестикутника, описаного навколо цього кола.

 

Відповіді до математичного диктанту: 

 

1.                  2.                    3.             

 

 4.                   5.               6.

 

 

 

ІІІ. Вивчення нового матеріалу

Для того щоб побудувати правильний многокутник, вписаний у коло, досить побудувати його центральний кут. У правильному шестикутнику такий кут дорівнює 60⁰, тому для побудови правильного шестикутника одну вершину А₁ на колі вибираємо довільно. З неї як із центра радіусом, який дорівнює радіусу кола, робимо засічку і дістаємо вершину А₂. Аналогічно будуємо інші вершини А_3,    А_4,      А_5,    А₆  і сполучаємо їх послідовно відрізками.

 

                                             

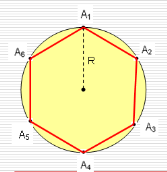
                                              Шестикутник

                                               А₁ А₂ А₃А₄А₅А₆ 

                                               вписаний у коло

 

 

 

 

 Для побудови правильного вписаного трикутника досить сполучити через одну вершини правильного вписаного шестикутника.

                                                     

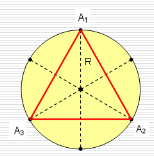
                                                    Трикутник

                                                     А₁ А₂ А₃

                                                    вписаний у коло

 

 

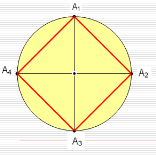
    Для побудови правильного вписаного чотирикутника досить провести через центр кола перпендикулярні прямі. Вони  перетнуть коло у вершинах квадрата.

 

                                                    Чотирикутник

                                                    А₁ А₂ А₃А₄

                                                     вписаний у коло

 

 

 

 

 

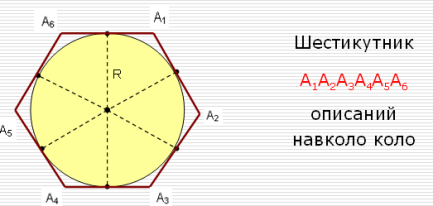
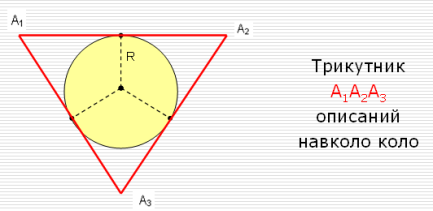
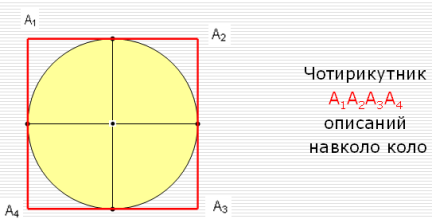
Для побудови правильного описаного многокутника досить провести дотичні до кола у вершинах правильного вписаного многокутника. Дотичні, що проходять через вершини правильного вписаного многокутника, перетинаються у вершинах правильного описаного многокутника.

 

 

 

 

VI. Розв’язування задач

Задача   (Слайд 22)

Сторона правильного многокутника дорівнює 12 см, а радіус описаного навколо нього кола дорівнює 10 см.

Знайдіть радіус вписаного кола.

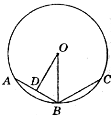                 Дано: многокутник;

                  АВ=ВС= 6 см; ОВ = R.

                   Знайти: ОD.

 

                               Розв’язання

OD = r; OD┴AB, отже . З трикутника ODB (ﮮD=90⁰) за теоремою Піфагора  

(Відповідь: 8 см.)

Задача   (Слайд 23)

У коло радіуса 4 см вписано правильний трикутник, на стороні якого побудовано квадрат. Знайдіть радіус кола, описаного навколо квадрата.

(Відповідь:           см.)

V. Домашнє завдання        (Слайд 24)

Опрацювати §11

Завдання 12

7(г);   8(в);   12(в);   20

IV. Підсумок     уроку          (Слайд 25)

1. Які багатокутники називаються правильними?
2. Який багатокутник називається описаним навколо кола?
3. Який багатокутник називається вписаним у коло?
4. Формули радіусі вписаних і описаних кіл правильних многокутників.
5. Як можна вписати в коло шестикутник?
6. Як можна вписати в коло трикутник?