Урок. Презентація. "Геометричні перетворення графіків функції"

Геометричне перетворення графіків функції 9-10 клас

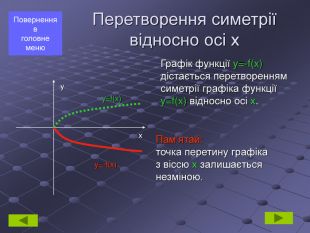
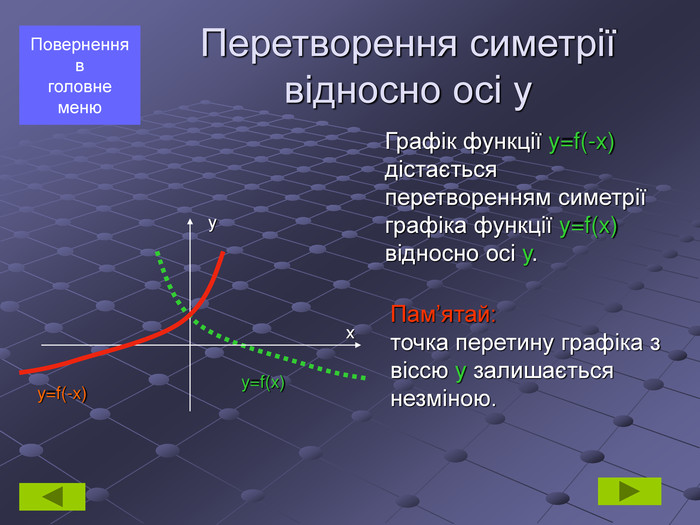
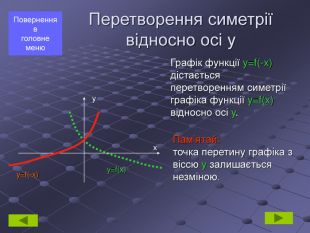
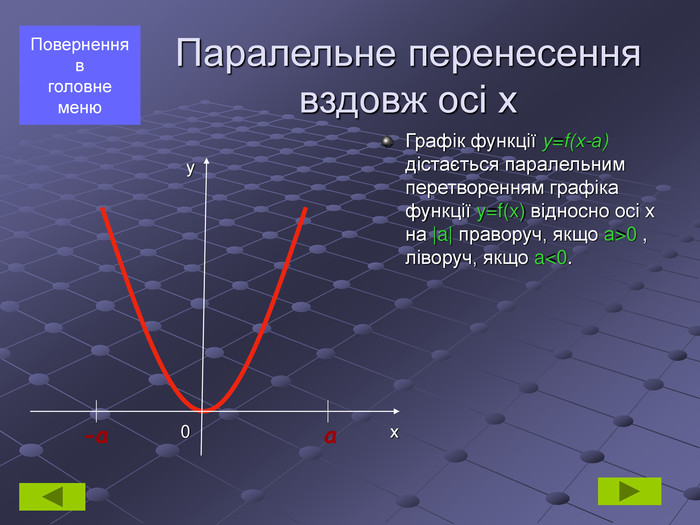
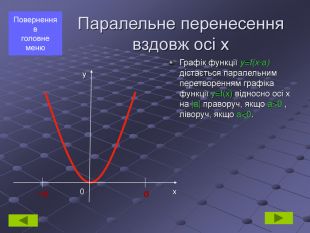
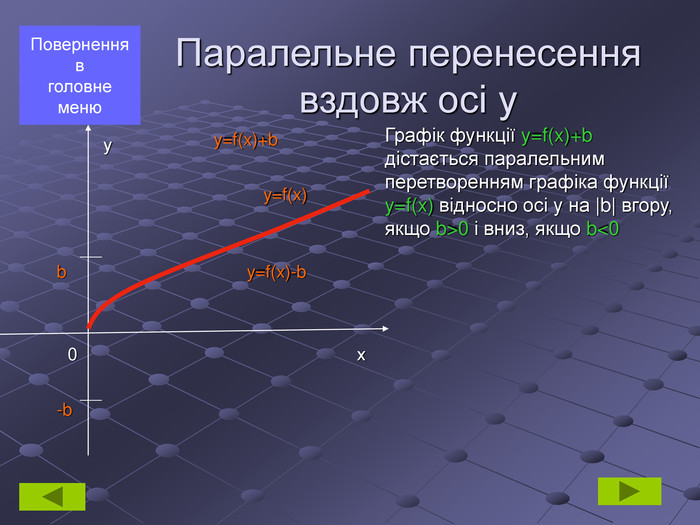
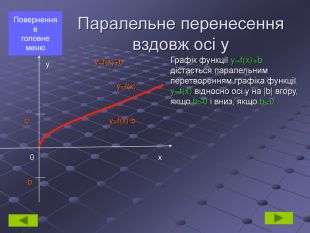
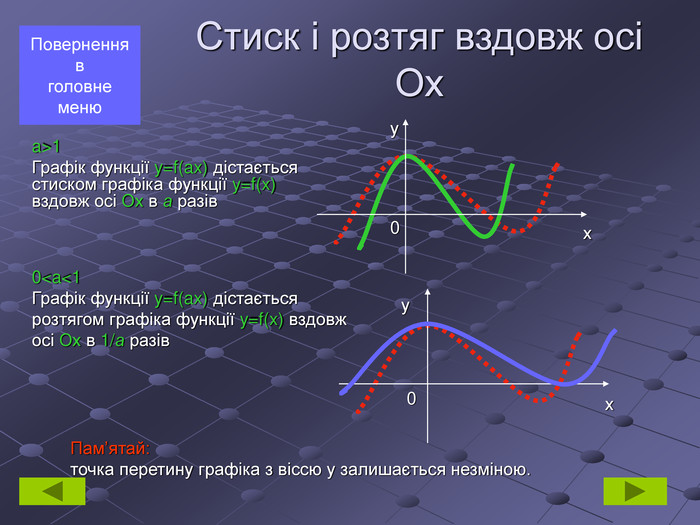
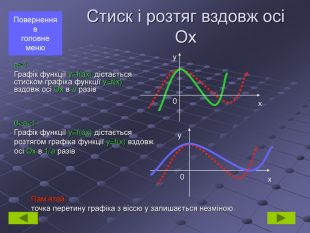
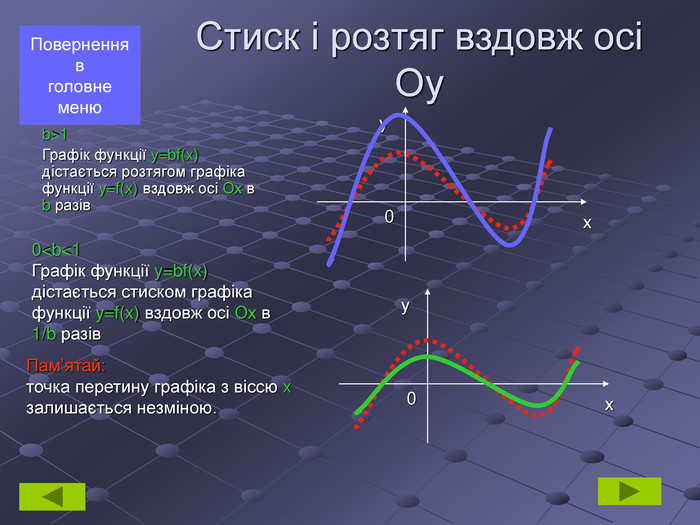
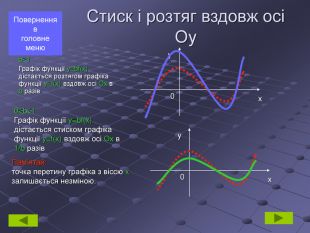
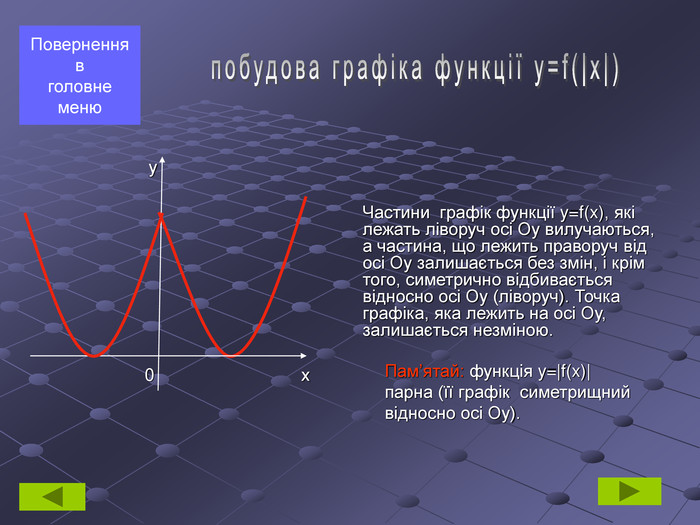
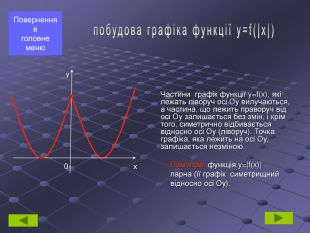
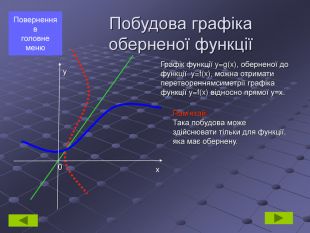
Перетворення симетрії відносно осі х Перетворення симетрії відносно осі у Паралельне перенесення вздовж осі х Паралельне перенесення вздовж осі у Стиск і розтяг вздовж осі Ох Стиск і розтяг вздовж осі Оу Побудова графіка функції y=|f(x)| та y=f(|x|) Побудова графіка оберненої функції Тестові завдання зміст

Повернення в головне меню y=-f(x) y=f(x) х у Пам’ятай: точка перетину графіка з віссю х залишається незміною. Перетворення симетрії відносно осі х Графік функції y=-f(x) дістається перетворенням симетрії графіка функції y=f(x) відносно осі х.

Повернення в головне меню Пам’ятай: точка перетину графіка з віссю у залишається незміною. у х y=f(-x) y=f(x) Перетворення симетрії відносно осі у Графік функції y=f(-x) дістається перетворенням симетрії графіка функції y=f(x) відносно осі у.

Повернення в головне меню 0 у х a -a Паралельне перенесення вздовж осі х Графік функції y=f(x-а) дістається паралельним перетворенням графіка функції y=f(x) відносно осі х на |a| праворуч, якщо а>0 , ліворуч, якщо a<0.

Повернення в головне меню b -b 0 y=f(x)+b y=f(x)-b y=f(x) у х Паралельне перенесення вздовж осі у Графік функції y=f(x)+b дістається паралельним перетворенням графіка функції y=f(x) відносно осі у на |b| вгору, якщо b>0 і вниз, якщо b<0

Повернення в головне меню 0 у х 0 у х 01 Графік функції y=f(ax) дістається стиском графіка функції y=f(x) вздовж осі Ох в а разів

Повернення в головне меню у х 0 у х 0 01 Графік функції y=bf(x) дістається розтягом графіка функції y=f(x) вздовж осі Ох в b разів

Повернення в головне меню Пам’ятай: функція y=|f(x)| невід”ємна (її графік розташований у верхній півплощині). 0 у х Побудова графіка функції y=|f(x)| та y=f(|x|) Частини графік функції y=f(x), які лежать вище осі Ох і на осі Ох, залишається без змін, а частини, які лежать нижче осі Ох—симетрично відбиваються відносно цієї осі (вгору)

Повернення в головне меню Пам’ятай: функція y=|f(x)| парна (її графік симетрищний відносно осі Оу). 0 у х Частини графік функції y=f(x), які лежать ліворуч осі Оу вилучаються, а частина, що лежить праворуч від осі Оу залишається без змін, і крім того, симетрично відбивається відносно осі Оу (ліворуч). Точка графіка, яка лежить на осі Оу, залишається незміною.

Повернення в головне меню 0 у х Пам’ятай: Така побудова може здійснювати тільки для функції, яка має обернену. Побудова графіка оберненої функції Графік функції y=g(x), оберненої до функції y=f(x), можна отримати перетвореннямсиметрії графіка функції y=f(x) відносно прямої у=х.

Start Повернення в головне меню Тестові завдання

перетворенням симетрії графіка функції паралельним перетворенням графіка функції дістається стиском графіка функції Як з графіка функції у=2х утворити графік функції у=-2х.

Графік функції дістається паралельним перетворенням графіка функції відносно осі Ох в ліво на 1, після чого паралельним перетворенням утворений графік функції переносимо відносно осі Оу вгору на 3. Графік функції дістається паралельним перетворенням графіка функції відносно осі Оу вгору на 3, і потім паралельним перетворенням відносно осі Ох вліво на 1 Графік функції дістається паралельним перетворенням графіка функції відносно осі Ох в ліво на 3, після чого теж паралельним перетворенням відносно осі Оу вгору на 1. Як можна побудувати графік функції

Напишіть функцію даного графіка

Дізнайся результат

З 4 можливих Stop Start Результати тестування