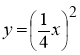Завдання для підсумкових контрольних робіт з алгебри
В роботі укладено по два варіанти завдань для підсумкових (семестрових, річних) контрольних робіт з алгебри для учнів 9 класу. Варіанти робіт містять тестові завдання, завдання на встановлення відповідності та завдання на повне розгорнуте розв' язання. Роботи укладено так, що можна використовувати для учнів, які вчаться в класах з поглибленим вивченням математики, адже в роботі є завдання з позначкою "м".
.
Підсумкова контрольна робота з алгебри за І семестр
9 клас
І варіант
1.Яка нерівність виконується при всіх значеннях змінних?
|
А |
Б |
В |
Г |
Д |
|
|
|х| – |у| ≥ 0 |
х2 + 1 0 |
(х – 5)2 0 |
х – у ≥ 0 |
2. Знайти область значень функції у = 
+ 4?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
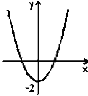
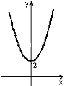
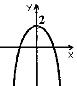
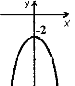
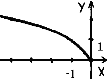
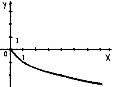
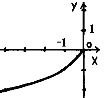
3.З-поміж наведених графіків укажіть графік функції у = – х2 +2
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4.Визначте напрям віток та координати вершини параболи у = –2х2 + 8х – 1
|
А |
Б |
В |
Г |
Д |
|
Вітки вниз, (–2; 7) |
Вітки вниз, (2; –25) |
Вітки вниз, (2; 7) |
Вітки вгору, (2; 7) |
Вітки вгору, (–2; –25) |
5.Побудуйте графік функції у = х2 – 8х – 9. Користуючись графіком, встановіть відповідність між названими проміжками (1-4) та числовими проміжками (А-Д), що їм відповідають:
|
1) |
проміжки зростання функції; |
А) |
|
|
2) |
проміжки спадання функції; |
Б) |
|
|
3) |
проміжки, на яких функція набуває від’ємних значень; |
В) |
|
|
4) |
проміжки, на яких функція набуває невід’ємних значень. |
Г) |
(–; –1] і [9; +); |
|
|
|
Д) |
|
6. Доведіть, що при всіх значеннях а і в виконується нерівність а2 + 8а - 10в + в2 + 42 0.
7. Знайти нулі функції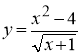 
.
8. Розв’язати нерівність │x - 3│ (х2 + 3х – 10) 0.
9.м Побудуйте графік функції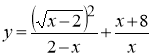 
.
Підсумкова контрольна робота з алгебри за І семестр
9 клас
ІІ варіант
1. Яка нерівність виконується при всіх значеннях змінних?
|
А |
Б |
В |
Г |
Д |
|
|
|х| + |у| ≥ 0 |
х2 – 1 ≥ 0 |
(х – 5)2 0 |
х – у ≥ 0 |
2. Знайти область визначення функції 
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. З-поміж наведених графіків укажіть графік функції 
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
4. Визначте напрям віток та координати вершини параболи. у = 2х2 + 8х – 1
|
А |
Б |
В |
Г |
Д |
|
Вітки вгору, (2; 23) |
Вітки вниз, (–2; –9) |
Вітки вниз, (2; 23) |
Вітки вгору, (–2; 7) |
Вітки вгору, (–2; –9) |
5. Побудуйте графік функції у = – х2 – 8х + 9. Користуючись графіком, встановіть
відповідність між названими проміжками (1-4) та числовими проміжками (А-Д), що їм відповідають:
|
1) |
проміжки зростання функції; |
А) |
|
|
2) |
проміжки спадання функції; |
Б) |
|
|
3) |
проміжки, на яких функція набуває від’ємних значень; |
В) |
|
|
4) |
проміжки, на яких функція набуває невід’ємних значень. |
Г) |
|
|
|
|
Д) |
|
6. Доведіть, що при всіх значеннях а і в виконується нерівність 10а2 – 6а +2а в + в2 +2 ≥ 0.
7. Знайти нулі функції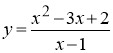 
.
8. Розв’язати нерівність (х -2)2 (х2 - 8х - 9) 0.
9.м Побудуйте графік функції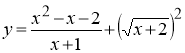 
.
Підсумкова (річна) контрольна робота
з алгебри
9 клас
І варіант
1. Знайти знаменник геометричної прогресії, якщо b1 = 4, а b3 = 1.
|
А |
Б |
В |
Г |
Д |
|
|
|
2 |
–2; 2 |
4 |
2. Знайти область визначення функції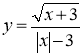 
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. Яка ймовірність того, що навмання назване натуральне двоцифрове число виявиться додатним?
|
А |
Б |
В |
Г |
Д |
|
|
0 |
1 |
|
|
4. Установити кількість розв’язків системи рівнянь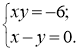 
|
А |
Б |
В |
Г |
Д |
|
1 розв’язок |
2 розв’язки |
4 розв’язки |
Розв’язків немає |
Безліч розв’язків |
5. Встановіть відповідність між геометричними перетвореннями графіка функції у = х2 (1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
|
1) |
графік функції у = х2 паралельно перенесли вздовж осі ОY на 1 одиницю вгору; |
А) |
у = (х – 1)2 |
|
2) |
графік функції у = х2 паралельно перенесли вздовж осі ОХ на 1 одиницю вліво; |
Б) |
у = х2 – 1 |
|
3) |
графік функції у = х2 паралельно перенесли вздовж осі ОY на 1 одиницю вниз; |
В) |
у = (х + 1)2 |
|
4) |
графік функції у = х2 паралельно перенесли вздовж осі ОХ на 1 одиницю вправо; |
Г) |
у = (х – 1)2 + 1 |
|
|
|
Д) |
у = х2 + 1 |
6. Розв’язати нерівність 
.
7. Скільки кілограмів 20-відсоткового і скільки кілограмів 50-відсоткового сплавів міді треба взяти, щоб отримати 30 кг 30-відсоткового сплаву?
8. Не виконуючи побудови, знайти точки перетину графіка функції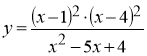 
з осями координат.
9.м При якому найбільшому цілому значенні а система нерівностей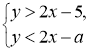 
має хоча б один розв’язок?
Підсумкова (річна) контрольна робота
з алгебри
9 клас
ІІ варіант
1.Чому дорівнює сума 10-и перших членів арифметичної прогресії (ап), якщо а1 = 4, а10= –16?
|
А |
Б |
В |
Г |
Д |
|
60 |
– 60 |
100 |
– 120 |
80 |
2.Знайти область визначення функції 
?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
3. Установити кількість розв’язків системи рівнянь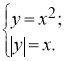
|
А |
Б |
В |
Г |
Д |
|
1 розв’язок |
2 розв’язки |
4 розв’язки |
Розв’язків немає |
Безліч розв’язків |
4. Замість * у число 134* поставили одну з непарних цифр. Яка ймовірність того, що отримане число буде ділитися на 4?
|
А |
Б |
В |
Г |
Д |
|
|
|
2 |
1 |
0 |
5. Встановіть відповідність між геометричними перетвореннями графіка функції у = х2 (1-4) та функціями, одержаними в результаті таких перетворень (А-Д):
|
1) |
графік функції у = х2 стиснули у 4 рази до осі ОY; |
А) |
|
|
2) |
графік функції у = х2 розтягнули у 4 рази від осі ОY; |
Б) |
|
|
3) |
графік функції у = х2 стиснули у 4 рази до осі ОХ; |
В) |
|
|
4) |
графік функції у = х2 розтягнули у 4 рази від осі ОХ. |
Г) |
|
|
|
|
Д) |
|
6. Розв’язати нерівність 
.
7. У першому бідоні було молоко з масовою часткою жиру 2%, а в другому – 5%. Скільки треба взяти молока з кожного бідона, щоб отримати 12 л молока, масова частка жиру якого дорівнює 4%?
8. Не виконуючи побудови, знайти точки перетину графіка функції 
з осями координат.
9.м При якому найменшому цілому значенні а система нерівностей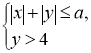 
має хоча б один розв’язок?
про публікацію авторської розробки
Додати розробку