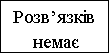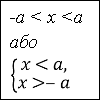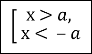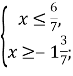Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною
Алгебра 9 клас
Методичні рекомендації до уроку
Тема уроку: Розв'язування систем (та сукупностей) лінійних нерівностей з однією змінною
Алгебра 9 клас
Методичні рекомендації до уроку
Тема уроку: Розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною
Мета уроку: закріплення учнями знань змісту понять: нерівність з однією
змінною та що означає розв’язати нерівність з однією змінною; система нерівностей з однією змінною, розв’язок системи нерівностей з однією змінною та що означає розв’язати систему нерівностей з однією змінною; сукупність нерівностей з однією змінною, розв’язок сукупності нерівностей з однією змінною та що означає розв’язати сукупність нерівностей з однією змінною, а також закріплення знань учнів про схеми розв’язування лінійних нерівностей з однією змінною, їхніх систем та сукупностей. Доповнення знань учні схемами розв’язування найпростіших нерівностей з модулем (з використанням геометричного змісту модуля), а також прикладами завдань на складання та розв’язування систем нерівностей з однією змінною (зокрема на знаходження ОД3 виразу). Виробити в учнів уміння : відтворювати зміст вивчених понять і використовувати їх для розв’язування практичних завдань.
Компетентності, що формуються: математична – уміння оперувати числовою інформацією, розв’язувати вправи, що передбачають розв’язування систем (та сукупностей) лінійних нерівностей з однією змінною; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; уміння вчитися впродовж життя.
Наочність та обладнання: підручник, опорний конспект, картки-підказки.
Тип уроку: удосконалення вмінь, відпрацювання навичок.
Хід уроку
- Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
- Перевірка домашнього завдання
Учитель перевіряє виконання роботи в учнів, що потребують додаткової педагогічної уваги (збирає їхні зошити для перевірки та за необхідності роздає матеріали для проведення корекційної роботи).
Фронтально можна провести роботу у формі гри «Знайди помилку» - запропонувати учням знайти у розв’язанні вправ домашнього завдання «помилки» (які вчитель навмисне зробив у запропонованому учням варіанті виконання домашнього завдання).. Цей вид роботи можна провести як в усній формі, так і у формі письмової самостійної роботи. В останньому випадку результати виконання роботи слід одразу ж перевірити (наприклад, у парах) та скорегувати; учнів, що впораються із завданням без помилок, слід заохотити відповідними оцінками.
- Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Результати (тобто припущені учнями помилки) виконання домашнього завдання та/або самостійних вправ на початку уроку, а також наступне обговорення припущених помилок дають можливість учням усвідомити необхідність продовження роботи з відпрацювання навичок застосування вивчених на попередніх трьох уроках алгоритмів.
Таким чином, удосконалення навичок розв’язування нерівностей з однією змінною та їхніх систем і сукупностей разом із вивченням сфери їх практичного застосування становить основну дидактичну мету уроку.
- Актуалізація опорних знань та вмінь учнів
Усні вправи
- Розв’яжіть нерівність:
-
3х>6; 2) –х≥-5; 3) –х≤0; 4)
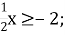 5)
5) 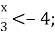 6) -
6) -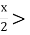 1,5.
1,5.
- Розв’яжіть систему нерівностей :
-
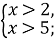 2)
2) 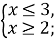 3)
3) 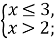
4) ![]() 5)
5)![]() 7)
7) ![]()
- Назвіть кілька чисел, що задовольняють умову:
- ׀х׀= 2; 2) ׀х׀> 2; 3) ׀х׀< 2.
- Доповнення знань
План вивчення нового матеріалу
- Розв’язування нерівностей виду ׀х׀<а.
- Розв’язування нерівностей виду ׀х׀>а.
- Приклади завдань на складання та розв’язування систем нерівностей з однією змінною.
Методичний коментар
Викладення питання про розв’язування найпростіших нерівностей з модулем ведеться традиційно та ґрунтується на геометричному змісті модуля (модуль числа – це відстань від початку відліку на координатній прямій до даної точки). Тому задля кращого розв’язуванням необхідно провести відповідну роботу з повторення знань та вмінь учнів щодо означення модуля числа та деяких властивостей модуля, а також щодо розв’язування лінійних нерівностей з однією змінною та їхніх систем і сукупностей (див. усні вправи вище).
Також традиційно розглядається питання про застосування систем рівнянь для розв’язування стандартної задачі на знаходження ОД3 виразу, що містить змінну під знаком арифметичного квадратного кореня.
Опорний конспект
|
Найпростіший нерівності з модулем
a≤0 a>0 a<0 a=0 a>0
Наприклад : Наприклад:
Приклад 1. Визначимо, при яких значеннях змінної має зміст вираз Розв’язання
Вираз
Відповідь:
Приклад 2. Розв’яжемо нерівність Розв’язання: Дана нерівність рівносильна системі:
Відповідь:
|
- Відпрацювання навичок. Удосконалення вмінь.
Усні вправи
- Кожну з нерівностей замініть рівносильною системою або сукупністю нерівностей:
- ׀х ׀> 3; 2) ׀х׀ < 3; 3) ׀х – 2 ׀≥ 2; 4) ׀х – 3 ׀≤ 1 .
- Розв’яжіть систему нерівностей:
-
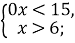 2)
2) 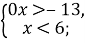 3)
3) 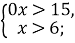
Письмові вправи
Методичний коментар
3міст вправ, винесених на поточний урок, так само, як і на попередніх уроках, має спрямування на вироблення навичок безпомилкового виконання таких дій:
- Рівносильні перетворення нерівностей з однією змінною;
- Розв’язування лінійних нерівностей з однією змінною;
- Розв’язування систем і сукупностей лінійних нерівностей з однією змінною;
- Розв’язування нерівностей виду ׀x׀<a шляхом розв’язування системи лінійних нерівностей з однією змінною;
- Розв’язування нерівностей виду ׀x׀>a шляхом розв’язування сукупностей лінійних нерівностей з однією змінною.
Цього можна домогтися за рахунок достатньо великої кількості вправ різного рівня складності. Для того щоб пожвавити цю одноманітну роботу, учитель може організувати її проведення у нестандартному вигляді , наприклад, у формі математичної естафети, математичного бою, або підготувати завдання на картках-підказках.
Під час усної роботи на уроках корисно пропонувати учням вправи на повторення цих моментів.
- Підсумки уроку
Учні виконують самостійну роботу № 4 у зошиті для самостійних і контрольних робіт.
- Домашнє завдання
- Вивчити схеми розв’язування нерівностей виду ׀x׀<a, ׀x׀>a.
- Виконати вправи на застосування вивчених схем.
- Повторити : зміст основних понять теми 1 та схем дій, вивчених у цій темі, а також скласти загальну схему, що відображає логічний зв'язок між питаннями теми; розв’язати вправи на застосування цих теоретичних положень (див. зміст вправ класної роботи).


про публікацію авторської розробки
Додати розробку