Урок-презентація теореми: "Сума кутів трикутника"

Урок №

Тема уроку: Сума кутів трикутника

Мета уроку: Довести теорему про суму внутрішніх кутів трикутника, показати її практичне застосування до розв’язування вправ. Розвивати навики узагальнювати, робити висновки, логічне мислення, графічну культуру, вміння вимірювати кути. Розширювати кругозір учнів, пізнавальні інтереси. Виховувати наполегливість, охайність, вміння працювати в парах, групах, оцінити рівень своїх досягнень.

Обладнання: креслярські прилади, транспортир, астролябія, портрети Г. Галілея, Піфагора, Чебишева, рисунки до задач, перфокарти, Мудра сова, ілюстрація „Страта Гіпатії”, „Жорсткість трикутника”, „Визначеня відстані до недоступної точки”, „Журавлиний ключ”, „Ейфелева вежа”, вірші, акровірш, піктограми настрою, пам’ятка для учнів, етимологічний словник.

Тип уроку: Урок вивчення нового матеріалу.

Форма проведення: Урок-презентація теореми.

 

Хід уроку

І.Створення позитивних мотивів навчання.

 І хоч надворі похмуро, а ви подаруйте посмішку один одному. Посміхніться і до наших гостей.

 Ми з вами на уроці геометрії. А з якими словами у вас асоціюються перші літери слова урок (слово „урок”).

 У-

 Р-

 О-

 К-

 А свої побажаня я вам хочу виразити словами акровіршу:

 Успіхів бажаю вам сьогодні,

 Робота радість хай вам принесе,

 Обдарованість ви покажіть на кожнім кроці,

 Кмітливість впевненості хай вам додає.

ІІ. Перевірка домашнього завдання. Актуалізація опорних знань

• Прошу чергових доповісти про виконання домашнього завдання.

- За допомогою піктограм настрою давайте з’ясуємо вашу оцінку вашої готовності до уроку.

• А зараз повторимо теоретичний матеріал.

1)Три точки ми поставимо,

Відрізками з’єднаємо.

Фігуру з вами маємо.

Її як називаємо? (трикутник)

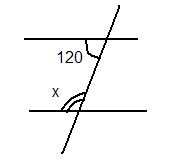2)Визначити невідомі кути на малюнках .

 

 

 

 

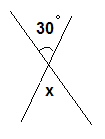
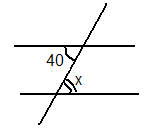
3) В яких одиницях ми з вами вимірюємо кут? ( В градусах) Слово градус латинського походження, що в перекладі означає „крок”.

4) А яким приладом вимірюють і будують кути ? (транспортир). В перекладі з латинської мови означає „ переносити”, тобто будувати такий самий кут.

5) По даному малюнку сформулювати відому аксіому.

 

 

 

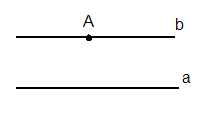
ІІІ. Мотивація пізнавальної діяльності учнів.

• Що я тримаю в руках ? (монета)
•                   А чи знаєте ви , що на островах Кука в Тихому океані  були монети трикутні, а не круглі. Але користувалися ними недовго, і всі 90 тисяч екземплярів осіли в кишенях нумізматів.

 Унікальний трикутник! Його величність Трикутник! (ілюстрація) Ми так говоримо, бо з ним мають справу  архітектори і будівельники, агрономи і психологи, закрійники і математики. Щоб досягти міцності і стійкості різних споруд, їх окремим деталям надають форми трикутника, тобто застосовують властивість трикутника, яка називається жорсткістю. Ця властивість використовується при будівництві мостових арок, перекритті в будівлях, при конструюванні підйомних кранів і опорних щогл електросітки високих напруг. (ілюстрація) Недаремно відомий італійський фізик і математик Г. Галілей говорив: „ Природа говорить мовою математики. Букви цієї мови: трикутники, кола та інші геометричні фігури ”. (портрет, вислів)

Тому то і треба знати трикутник досконало. А скільки теорем пов’язано з ним! Неможливо всі перерахувати! І сьогодні у нас з вами перша така теорема шкільного курсу геометрії. Тому і урок можна назвати: урок –презентація теореми „ Сума кутів трикутника”.

-Записали дату та тему уроку.

Ян Амос Коменський, відомий чеський педагог, говорив: „ Вважай нещасливим той день чи час, коли ти не засвоїв нічого нового, не добавив до своїх знань ”. Тому будьте на уроці (пам’ятка для учня):

- уважними

- активно пізнавайте нове,

- будьте наполегливими і не бійтеся помилитися,

- учіться відчувати радість відкриття.

 Бо завдання на уроці треба реалізувати такі (надруковані окремо на кожну парту):

• шляхом досліджень і узагальнення сформулювати теорему та довести її,
• показати практичне застосування до розв’язування вправ,
• розвивати графічну культуру, вміння аналізувати , робити висновки.

ІV. Вивчення теоретичного матеріалу .

1.Завдання в парах (практична робота). Для кожної пари накреслено окремо трикутник.

Виміряти кути трикутника та знайти їх суму. Зробити висновок.

  Їх в геометрії багато

  І всі їх треба добре знати.

  Які б ми не вивчали теми,

  Ми скрізь зустрінем теореми.

2 Підручник .с.81 теорема 8.

    3.Доведення теореми (вчитель)

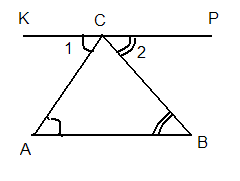                                                                           Дано: ∆АВС,

                                                                            Довести :

 

 

 

 

                                                   Доведення

Проведемо КР ║АВ. (Скільки можна провести прямих, паралельних до даної через точку С?) ( як внутрішні різносторонні кути при паралельних прямих).

.

Тому ,

.

Що й треба було довести.

3.Але дану теорему можна довести і іншим способом._________ мала завдання підготувати інше доведення теореми з іншого шкільного підручника. (випереджальне завдання).

 

 

 

 

 

 

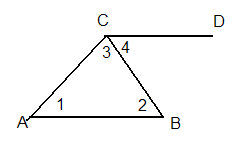
                                                Доведення

 Проведемо CD ║АВ.

, як внутрішні односторнні кути при паралельних прямих. Але є сумою та. Тобто ,тепер маємо . Але , як внутрішні різносторонні кути при паралельних прямих.

Тому .

 Що й треба було довести.

4. Дана теорема була відома ще в стародавньому Єгипті, проте доведення цього факту було дано значно пізніше. Вважають, що його дав Піфагор, (портрет) грецький математик, про якого ми більш детально будемо говорити в 8 класі, доводив цю теорему за допомогою паперових моделей.

 

 

 

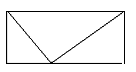
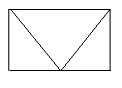
V. Застосування теоретичного матеріалу у стандартних умовах

 Теорія залишається мертвою, якщо вона не знаходить свого практичного застосування. Відомий російський математик Пафнутій Львович Чебишев говорив: „ Недостатньо знати всі теореми та правила, треба вміти ними користуватися ”(Вислів та портрет)

1.Усні вправи по готових малюнках.

 

 

 

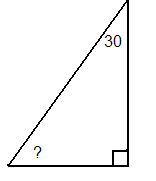
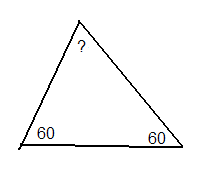
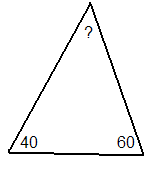
2.

• Чи може в трикутнику бути два тупих кути ?
• Чи може в трикутнику бути два прямих кути ?
• Чи може в трикутнику бути прямий та тупий кути ?

Книга .С.81.Наслідок.

3.Вправа. (Мудра Сова)

  Мудрий птах летів до вас,

  А надворі дощ якраз.

  Всі рядки там намочились,

  І в них плями утворились,

  То ж давайте поміркуємо

  Й плями швидко ліквідуємо.

(Велика таблиця на дошці. Кожен учень заповнює таку ж таблицю). Коментують заповнення ланцюжком.

Дану таблицю вклеїти в зошити вдома.

Але це завдання не просте , а з секретом.

 

 Розгадати секрет вам допоможе код.

 

 

 

 

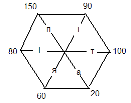
 Гіпатія – жінка математик, яка була автором приладу для вимірювання кутів на місцевості, а також кутів, що утворюють небесні світила, який називається астролябія.(Демонстрація астролябії)

 Слово астролябія грецького  походження , що в перекладі з грецької мови означає „зірка „ і „ручка”. Про трагічну долю цієї жінки розповість .......

Повідомлення учениці

    Гіпатія (370-415) народилася та жила в Александрії в епоху, коли реакційні сили особливо жорстоко переслідували науку.

    Вона була дочкою александрійського математика Теона. Займалася складанням астрономічних таблиць. Гіпатія винайшла пристрій для визначення густини рідини – ареометр і астролябію -- прилад для визначення довготи в астрономії та кутів на місцевості.

    У 412 році єпископом Александрії став Кирило-фанатик. Особливо він не любив членів гуртка, яким керував Гіпатія. І коли в місті вбили одного християнина, він розпустив чутку, що це зробили члени її гуртка.

   У березні 415 році натовп християн-ченців зупинив колісницю, на якій Гіпатія поверталася після лекції додому. Її поволокли у храм Кесоріон. Озвіріле збіговисько фанатів зірвало з жінки одяг і почало здирати устричними черепашками живу тканину тіла. А потім осатанілі спалили те, що залишилося від прекрасного людського тіла.

(Ілюстрація)

     Сучасник Гіпатії Паладас Александрієць присвятив їй рядки:

    Коли тебе бачу й слова твої чую,

    Молюся на тебе мов на святую,

    І зір мій у зоряне небо пливе,

    Де панна у зоряній небі живе.

    Усе що ти чиниш, Гіпатіє-зоре,

    Нам вказує небо твої разговори –

    Освіти широкої ясні моря

    Та мудрості незамутима зоря.

Астролябія допомогає визначити два кути на місцевості, рулетка - знайти відстань між двома об’єктами, теорема, яку ми вивчили – визначити третій кут, а вже потім знайти висоту предмета, відстань до недосяжного об’єкта. Це ми з вами будемо вивчати в 8, 9 класах на уроках геометрії. Але без знання сьогоднішньої теореми там не обійтись. (ілюстрації)

4.Робота в групах.

- Ваше завдання визначити невідомий кут , позначений на малюнку літерою х. Відповідати від групи буде той, хто витягне з скриньки червоного жетона. Тому навчити знаходити кут ви повинні кожного члена групи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

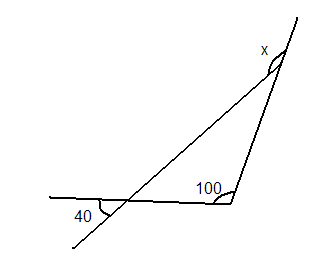
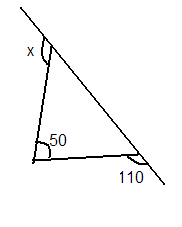
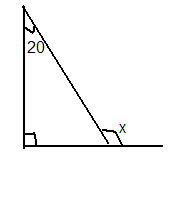
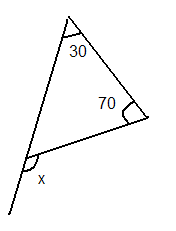
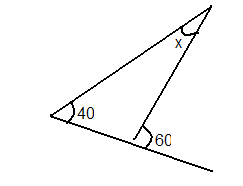
С.84.№297 (а)

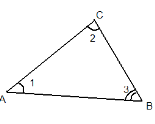Дано: ∆АВС,, на 30◦ менший    за

                                                          Знайти :.

 

 

 

                                   Розв’язання

 Нехай , тоді , а . За теоремою 8 .

 х+х+х+30=180,

          3х+30=180,

           3х=150,

            х=50.

Отже,.

   Вправа. Знайти , якщо АD – бісектриса , .

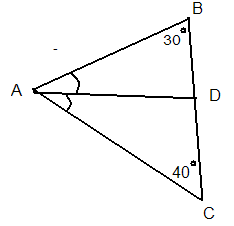
    Дано : ∆АВС,

   АD – бісектриса , .

  Знайти:

 

 

 

 

                                           Розв’язання

 Нехай , тоді . Маємо рівняння:

                                  х+х+30+40=180,

                                   2х=110,

                                     х=55.

Відповідь:55◦.

 А який інший спосіб розв’язання даної задачі? (180-(30+40)):2.

      Цей кут особливий. Цікаво, що журавлиний ключ будується так, що його сторони утворюють кут 110◦. Отже, лінія, що визначає напрям польоту і одна з сторін ключа утворюють кут 55◦. (Ілюстрація). Приблизно такий кут утворюють грані кристалів алмазу - 54◦45'.

 Кожна нога Ейфелевої вежі в Парижі спрямована до сторін горизонту під кутом 54◦. Мабуть, величину цього кута підказали міркування, пов’язані з завданнями надати цій споруді найбільшої міцності і стійкості.(Ілюстрація)

 

VІ. Рефлексія пізнавальної діяльності.

 А зараз ми з вам перевіримо, чи були хвилини нашого спілкування щасливими для вас і чи поповнили ви свої знання.

 Проведемо графічний диктант.(∩- так,  --- - ні).

1. Сума кутів трикутника 180◦.

2. В трикутнику може бути два прямих кути .

3. В трикутнику не може бути два прямих кути.

4. Кути трикутника  90◦, 60◦, 30◦.

5. Кути трикутника 100◦, 60◦, 40◦.

Взаємоперевірка в парах. Готовий графічний рисунок. ∩ - ∩ ∩ - . Повернути зошити товаришів.

• Чи задоволені ви своєю роботою на уроці? (піктограми настрою)
• А я задоволена роботою  ......................................

VІІ. Підсумок уроку.

Про французького математика Блеза Паскаля (портрет) говорили , що „ він носив у душі вир без дна ”. Блез народився у сім’ї математика. Він був хворобливим хлопчиком і тому батько до 12 років не дозволяв займатись йому математикою, щоб не нашкодити здоров’ю. У 12 років Блез довідався про геометрію і став одна за другою, граючись, доводити теореми.             

  Одна з них про те, що сума кутів трикутника дорівнює двом кутам столу.

 Чому він так її сформулював?

 А вам самий раз зайнятися геометрією і досягти певних результатів.

VІІІ. Домашнє завдання.

            §10(с.81) №296, 294(а).

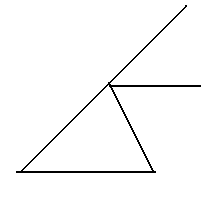
            *Довести теорему по готових малюнках