Урок Прикладні задачі з математики

Для позакласної і гурткової роботи великий інтерес викликають нестандартні геометричні задачі, в яких треба встановити максимальні і мінімальні величини (відстані, площі, периметри, об’єми і таке інше), а й задачі в яких слід виконати дослідження, які є прикладною моделлю досліджуваного явища, результати розв’язання яких можна використати на практиці. Такі задачі часто виникають безпосередньо у практичній діяльності людини, зокрема: при спорудженні будинків, будівництві доріг, мостів, вантажоперевезеннях і т.ін.

До розв’язання екстремальних задач вперше приступили швейцарський математик Якоб Штейнер і видатний німецький аналітик Лежен Діріхле в першій половині ХІХ ст. Вони продемонстрували нестандартні підходи до розв’язання таких задач, показали гнучкість уяви і мислення. Оскільки розв’язання таких задач вперше «стиналися на ноги», то було багато аналітиків для яких таке розв’язання (пояснення) було не прийнятним. Вони були схильні до непрямих розв’язань.

Одним з неприхильників такого підходу був німецький математик Карл Вейєрштрас. В 2-й половині ХІХ століття він піддав гострій критиці методи розв’язання Штейнера і Діріхле. Його критика не була безслідною, а була тим зерном з якого у майбутньому виросла наука топологія.

Нестандартних, різнопланових екстремальних задач в геометрії  досить багато. Розглянемо деякі з них.

Задача 1. У прямокутному трикутнику проведено висоту до гіпотенузи і вписано коло. Якого найбільшого значення може набувати відношення висоти до радіуса.

Розв’язання

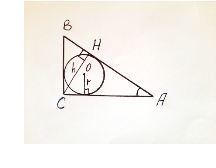Нехай катети трикутника будуть a i b, а гіпотенуза – с, тоді , а

.

Якщо

тоді .

;

Введемо функцію .

Дослідження виконаємо з використанням похідної.

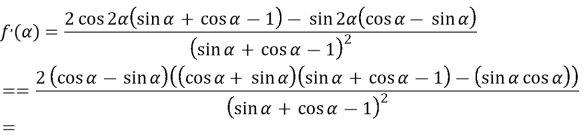
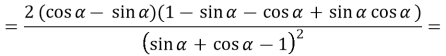
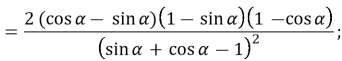
тому

 коли , оскільки – гострий кут. (

- точка max

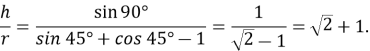
Відповідь:

Покажемо інший шлях дослідження відношення . За умовою це відношення повинно набувати найбільшого значення, тому відношення повинно бути найменшим.

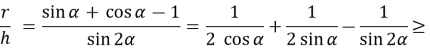
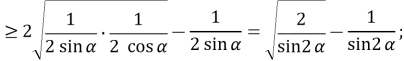
Нехай , ,

тоді )

Функція  при спадає,

а функція , при зростає, тому досягає мінімуму при х=1.

Отже ,  

,   тоді .

Відповідь:

Покажемо ще один спосіб розв’язання.

тоді .

 Звідси  .

Залишається оцінити вираз В довільному трикутнику .

З іншого боку .

.

Тобто , тому

Рівність досягається тоді, коли . Нарешті

Тому найбільше відношення

Відповідь:

Задача 2.

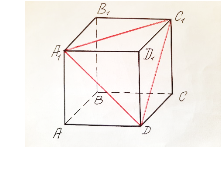
Яку найбільшу і найменшу тінь може відкидати куб, при паралельному проектування, ребро якого дорівнює а.

Розв’язання

Зрозуміло, що найменшу тінь ми одержимо тоді, коли грань куба буде паралельна площині проекції. Площа цієї тіні буде

Якщо площа перерізу куба площиною буде найбільшою і ця площина перерізу буде паралельна площині проекції, то ми одержимо найбільшу тінь. В перерізі січної площини і куба можуть бути: трикутники, чотирикутники, п’ятикутники і шестикутники. Очевидно, що найбільшу площу треба шукати серед шестикутників. Оскільки протилежні грані куба паралельні, то протилежні сторони шестикутника також паралельні. має найбільшу площу серед усіх перерізів трикутної форми. Якщо площина проекції паралельна площині , то куб відкидатиме тінь у вигляді правильного шестикутника, площа якого у 2 рази більша площі  .

Ребро куба а, тоді   .

Відповідь: , .

Задача 3. Поблизу заводу А по наміченій прямі до міста В прокладено залізничну колію. Під яким кутом до залізничної колії треба прокласти шосе, щоб із заводу А до міста В перевезення вантажу було найдешевшим, якщо вартість перевезення однієї тонни по шосе вдвічі дорожче, ніж по залізниці?

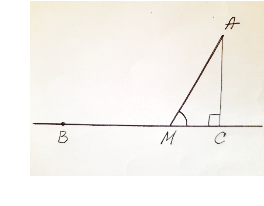Розв’язання

Введемо позначення AC=d, BC=a, AM=2x, BM=x. Оскільки перевезення по шосе в 2 рази дорожче, то сума х+2у=m, повинна набувати найменшого (найдешевшого) значення.

Маємо

Піднесемо до квадрату обидві частини рівності (вони додатні)

Значення у існує тоді, коли а щоб m набувало найменшого значення треба щоб ,

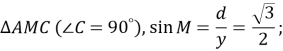
Відповідь: .

Пропоную завдання для самостійного опрацювання.

№1

В середині кута вибрано довільну точку. Через цю точку провести пряму, яка перетинає сторони кута і відтинає трикутник:

а) найменшої площі; б) найменшого периметра.

№2

Дві сторони дорівнює а і b. В яких межах може змінюватись величини:

а) найбільшого кута трикутника; б) найменшого кута трикутника.

№3

В середині трикутника (опуклого чотирикутника) знайти таку точку, щоб сума відстаней від цієї точки до вершин була найменшою.

№4

При вирубці лісу в недоступних місцях його сплавляють по ріках. В одному місці річка змінює своє русло під прямим кутом і ширина річки в цьому місці різна. Якої найбільшої довжини можна сплавити колоду, щоб вона не застрявала на повороті. Товщиною колоди можна знехтувати.

№5

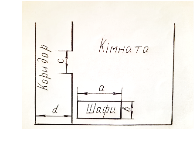Виконуючи ремонт у квартирі нам потрібно переставити речі або виносити їх із кімнати у коридор, або навпаки. Які найбільші розміри може мати шафа, щоб не розбираючи її, можна було б винести із кімнати у коридор. (Див. рис.)

Розв’язання цих задач буде опубліковано в наступних номерах журналу.