Урок–проект «Методи розв'язування показникових і логарифмічних рівнянь і нерівностей»

Урок – проект        «Методи розв'язування показникових і логарифмічних рівнянь і нерівностей»

Учасники проекту: учні   11 класу.

Тип проекту: інформаційно – дослідницький та практично – орієнтований.

Термін виконання: один місяць.

 Актуальність проекту як навчальної технології.

     Проектне навчання   сприяє розвитку учня як творчої і активної особистості, створює ефективні умови для розвитку компетенцій.

     Учні  набувають досвіду розв'язання реальних проблем у навчально – виховній діяльності. Робота над проектом розвиває творчі здібності, уяву. Створює умови для розвитку індивідуальних і творчих сил та здібностей учнів за інтересами та їх  реалізації.

 Мета і завдання проекту: узагальнити і систематизувати знання  вміння по темі; активізувати пізнавальну діяльність учнів, сприяти розвитку інтелектуальних і творчих здібностей, розвивати навички мислення, формувати вміння генерувати ідеї, розвивати пам'ять та обчислювальні навички. Надати можливість продемонструвати власні здібності і вміння переконувати.

Очікувані  результати: Вироблення в учнів умінь працювати з додатковою літературою, інтернетом, поєднувати різні джерела інформації, систематизувати матеріал, робити висновки, висловлювати свою думку. Вміти аргументовано її довести, бути толерантним у спілкуванні. Уміти використовувати нові інформаційні технології, удосконалювати вміння робити презентації і захищати їх.

Обладнання: картки, записи на дошці, комп'ютер, мультимедійний проектор, екран.

                                          Хід уроку

Ⅰ. Організаційно – підготовчий

1. Поділ класу на шість груп.
2. Визначення теми, мети і завдань проекту.
3. Розподіл завдань між членами групи.
4. Збирання інформації, робота з літературою, інтернетом.
5. Кожна група презентує свій проект. Учасники інших груп записують до своїх  зошитів запропоновані алгоритми і приклади розв'язування.
6. На проект можна взяти 2 спарених урока або спочатку розглянути проекти по показникової функції а на іншому  -  проекти по логарифмічній функції.

ⅠⅠ. Актуалізація опорних знань

Фронтальне опитування

1. Що називають функцією? Які види функцій ви знаєте?
2. Що називають областю визначення функції?
3. Яку функцію називають зростаючою? спадною?

        

Захист міні – проекту Ⅰ групою

Перша група нагадує означення та основні властивості степеня із ірраціональним та раціональним показником  (демонструючи на екрані властивості із натуральним та цілим показником ).

Дає означення показникової функції її властивості та графік функції. 

Розглядає приклади використання властивостей  показникової  функції.

Порівняйте   x   і   y, якщо:  1)    ;   2)    .

Порівняйте   числа   1) і    ;  2) і  .

Обчисліть   1)   ´;   2) .

Показникова функція часто використовується для описання різних  фізичних процесів, наприклад, радіоактивний розпад описується формулою:

                        m(t) = m˳

де  m˳- маса радіоактивної речовини в початковий момент часу t = 0,  m(t)  - її маса в момент часу  t,   T˳ - період напіврозпаду ( інтервал часу, за який початкова кількість речовини зменшиться вдвічі ).

Задача. Період напіврозпаду деякого ізотопу дорівнює 140 діб. Скільки плутонія залишиться через 4 роки, якщо його початкова маса дорівнює 10 г?

Розв'язання.  Маємо m˳ = 10 г,  t = 3·365 + 366 = 1461 (діб ).

 Тоді  m (1461) = 10 · ( 0,0072 г.

Відповідь. 0,0072 г.

По закону показникової функції якби  макові зерна всі проростали, то через 5 років число «потомків» однієї рослини було б  243 · або приблизно 2000 рослин на 1суші.

Потомство  пари мух за  два роки мало б масу що перевищує масу земної кулі.

В природі, техніці і економіці зустрічається багато процесів, в яких значення величини міняється в одне і те саме кількість разів, тобто по закону показникової функції.

 

 

Захист міні – проекту Ⅱ групи

 

Логарифмом додатного числа b за основою  a, де  a   0,  a   називається показник степеня, до якого треба піднести  число a, щоб одержати b.

Позначається  .

Слово логарифм походить  від грецьких  « logos» - слово, вчення і « arithmos» - число, лічба.

Розповідають про десятковий та натуральний логарифми.

Виводять основну логарифмічну тотожність, дають  означення логарифмічної функції, називають основні властивості логарифмічної функції, використовуючи  таблиці і проектор.

Розв’язують  вправи на дошці використовуючи властивості логарифмів,  степенів та логарифмічної функції.

 

 

 

 

 

 

 

 

 

 

Порівняйте: 1)  і  ;  2)  і  .

Порівняйте з одиницею основу логарифма, якщо: 1) > ;  2) < .

Обчисліть значення виразу: .

Розв’язання. = · = · = 9 · = 9 ·2 = 18.

Відповідь. 18.

Логарифмічну функцію  широко застосовують для опису реальних процесів. Логарифмічна функція моделює процеси швидкого зростання або затухання, тривалості хімічної реакції , а також зміни роботи газу, зміни сили відчуття від сили збудження ( психофізичний закон Вебера ).  Молюски, равлики мають панцирі завиті логарифмічною спіраллю. На рогах гірських козлів ніде не знайдете вузлів, бо вони завиті логарифмічною спіраллю. У соняха насіння також закручено по логарифмічній спіралі.

Захист міні – проекту ⅠⅠⅠ групою

Дають означення показникового  рівняння. Розв’язування  показникових рівнянь виду = b та  = b  шляхом зведення обох частин рівняння до спільної основи.

Розв'яжіть рівняння: 1)  =  ; 2) · = 3.

Розв'язання. 1)  =   = ;  =;  = ; х = 1.

                      2)  ·= 3.   ( = ;  ( = ;   ( = (;  х = .

Відповідь. 1)1 ; 2) .

Методи розв'язування показникових рівнянь.

1. Винесення спільного множника за дужки: 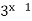 + 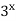= 12.

 Розв'язання.   · + = 12;    ( + 1 ) = 12 ;  · = 12 ;  ;  = 9 ;           = ; х = 2.

Відповідь.  2.

2. Спосіб зведення до квадратного: 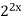 – 3 ·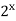 + 2 = 0.

 Розв'язання: Нехай = t,  t > 0.  – 3t + 2 = 0, за теоремою, оберненою до теореми Вієта, маємо: t₁ = 2 , t₂ = 1. Отже : = 2; х₁= 1. = 1; х₂ = 0.

Відповідь. 0; 1.

3. Приклади розв'язування  рівнянь, для  яких використовуються спеціальні прийоми: = .

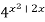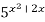Розв’язання. = . Поділимо обидві частини рівняння на  ≠ 0;   = 1;

( =( ;  + 2x = 0;   x ∙ ( x + 2 ) = 0;  x₁ = 0; x₂ = -2.

Відповідь. x₁ = 0,  x₂ = -2.

Захист міні – проекту  Ⅳ групою

Дають означення логарифмічного рівняння.

Розв’яжіть рівняння::  1) = - 1;  2) = -2.

Розв’язання. 1) = - 1; x = ;  x = .

                      2) = -2;  = ;  + 3x – 4 = 0;  x₁ = -4; x₂ = 1.

Відповідь. 1) ; 2) -4; 1.

  Називають основні методи розв’язань логарифмічних рівнянь. Наводять приклади.

1. Рівняння 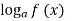=  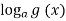  рівносильне  системі

     або 

з нерівностей  f(x) 0  або  g(x) > 0  вибираємо ту, яка є простішою.

Розв’яжіть рівняння = .

Розв’язання. Рівняння рівносильне системі :                      

Розв’язуючи рівняння   - 5x + 6 = 0, маємо x₁ = 3,  x₂  = 2.  Перший  корінь задовольняє умову х₁ > 2, а другий  - ні. Отже, х = 3 – єдиний корінь рівняння.

Відповідь. 3.

2. Рівняння виду 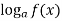= g(x) рівносильне рівнянню f(x) = .

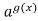Розв’яжіть рівняння -20) = х + 1.

Розв’язання. Дане рівняння рівносильне рівнянню:   - 20 = ;   ∙ - ∙ = 20;        ∙ ( 25 – 5) = 20;  ∙ 20 = 20;  = 1;  х = 0.

Відповідь. 0.

3. Рівняння, які зводяться до простіших за допомогою властивостей логарифмів.

Розв’яжіть рівняння + = 2.

Розв’язання. Область допустимих значень : х > .

Використовуючи формулу = +   справо наліво, маємо

= 2. Тоді  ( х + 1) ( 2х – 1) = ;  2 + х – 10 = 0 ;  х₁= 2;  х₂ = - 2,5.

Область допустимих значень задовольняє лише перший корінь.

Відповідь.2

4. Заміна змінних у логарифмічних рівняннях.

Розв'яжіть рівняння  + 3 – 4 =  0.

Розв'язання. Нехай  = t, тоді + 3t – 4 = 0 ;  t₁= - 4;  t₂ = 1.

Тоді = - 4;  х – 2 =   ;  х₁  = 2    або  = 1;  х – 2 = ;  х₂= 7.

Відповідь. 2 ; 7.

 

Захист міні – проекту Ⅴ групи

Дають означення  показникової нерівності,  схему розв’язання найпростіших  показникових нерівностей :

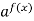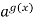
1. Якщо a > 0, то > 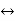f(x) > g(x) ( знак нерівності зберігається)
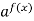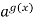
2.  Якщо 0 < a < 1, то > 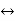f(x) < g(x) ( знак нерівності змінюється )

Розв’яжіть нерівність.1) 0,25; 2) ( ( ; 3) ( – 4 ∙ ( + 3 < 0.

Розв’язання. 1) Оскільки 0,25 = = , то .  Функція y = – зростаюча, то х - 1.

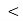
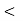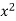2. Оскільки 0 1, то – 2х 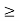х + 4 ; 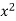– 3х - 4 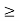0. Розв’язавши цю нерівність, отримуємо х 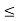- 1 або  х 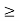4.
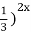3. ( – 4(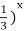 + 3 < 0. Нехай ( 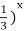= t, тоді 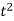– 4t + 3 < 0 .Розв’язавши останню нерівність, маємо 1 < t < 3 .Повернувшись до змінної х маємо: ( 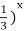> 1; х < 0 та ( 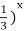< 3; х > - 1.
4. Відповідь. 1) х 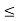- 1;  2) х 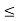- 1 або  х 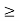4;  3) – 1 < х < 0.
5.  

 

Захист міні – проекту ⅤⅠ група

Дають означення  логарифмічної нерівності .Звертають увагу на те, що добре знати:

1. Загальні властивості нерівностей (перелічують з демонстрацією на екрані).
2. Властивість  монотонності логарифмічної функції.
3. Демонструють як знаходити область визначення логарифмів.
4. Демонструють опорну схему розв’язування  найпростіших логарифмічних  нерівностей.

 

>

 

                                                   Якщо a > 1, то 

 

Якщо 0 < a < 1,  то 

Звертають увагу на те, що під час розв’язування логарифмічних нерівностей необхідно обов’язково  враховувати область допустимих значень змінної.

Розв’яжіть нерівність: 1) < 0;  2) > 1;  3) 1; 

                            4) + – 2 0 .

Розв’язання. 1) < , х - <1,  - + х +1 < 0 при всіх дійсних значеннях х. Враховуючи  область допустимих значень змінної, маємо  - – х > 0,  х є ( 0; 1 ).                       2) > 1;  > ;  х + 1 > 5;  х > 4.

 3)  < ;  х + 7 > ;   х > - 6 .

 4) Нехай = t . Тоді  + t – 2 0, розв’язавши нерівність, маємо t - 2 або  t 1. Розглянемо - 2;  х ;  х 4 або 1;  0 < х 0,5.

Відповідь. 1) х є ( 0; 1 );  2) х > 4;  3) х > - 6 ;  4) 0 < х 0,5 або х 1.

 Ⅲ. Оцінювання міні – проектів і роботи учасників груп.

Проект

1. Якість змісту, чіткість викладу;
2. Глибина  розуміння матеріалу;
3. Наявність алгоритму  його чіткість і зрозумілість.

 

Картка самоконтролю

(оцініть себе за кожним з визначених напрямків від 0 до 2 балів )

Прізвище та ім’я		Кількість балів	Оцінка капітана групи
1	Я брав (ла) активну участь в роботі групи
2	Мої пропозиції були цікавими для  групи
3	Я брав(ла) участь у підготовці до виступу
4	Я можу самостійно застосувати отримані знання
5	Я засвоїв (ла) даний матеріал
6	Я захищав роботу перед класом

 

 Ⅳ. Вихідна рефлексія.

1. Що нового дізнались? Чому навчились7
2. Що сподобалось?
3. Що викликало  найбільші труднощі?
4. Над чим попрацювати вдома?
5. Що на сьогоднішньому уроці найважливішим відкриттям було…

 Ⅴ. Домашнє завдання.

Завдання для перевірки знань за підручником.