Урок. "Пропорції." Застосування “ Золотого перерізу”
Урок математики в 6 класі.
( Доцільно проводити в кінці навчального року, при повторенні навчального матеріалу.)
Тема: Повторення. Пропорції.
(Застосування “ Золотого перерізу”)
Мета:
- Повторення і узагальнення матеріалу з теми «Пропорції».
- Познайомити учнів із застосуванням відношення «золотого перерізу».
- Виховувати інтерес до математики через показ практичного застосування математичних знань в житті людини.
- Формувати навички самоконтролю, взаємоконтролю, увагу, наполегливість.
- Розвивати логічне і творче мислення.
Хід уроку:
Вступне слово вчителя.
Сьогодні на уроці ми будемо розв'язувати вправи та задачі на відношення та пропорції, а також познайомимося із застосуванням «золотого перерізу», яке ви зможете зрозуміти завдяки набутим знанням.
У кожного із вас на парті є конверт, у якому вкладені всі необхідні картки для сьогоднішньої роботи. Із конверта достаньте листок оцінювання, на якому ви будете виставлять кількість зароблених балів на кожному етапі роботи.
I. Перевірка домашнього завдання.
Проводиться взаємо перевірка за записами, вивішеними на дошці. Оцінка виставляється в лист оцінювання.
ЛИСТ ОЦІНЮВАННЯ
Прізвище клас
|
№ |
Виконана робота |
Кількість балів |
Примітки |
|
1 |
Домашня робота |
|
|
|
2 |
Усний рахунок |
|
|
|
3 |
Командна робота |
|
|
|
4 |
Робота біля дошки |
|
|
|
5 |
Самостійна робота |
|
|
|
6 |
Кросворд |
|
|
II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ.
Достаємо з конверта картку, з вправами для усного рахунку. За дві хвилини необхідно розв'язати найбільшу кількість прикладів.
Вправи для усного рахунку
І варіант
|
а) 7+0,2 : 6 ·2 -1,4 ? |
б) 10.9-1 : 3 ·2 -5.6 ? |
в) 6-2,4 : 6 ·3 +0,2 ? |
г) 40 ·0,4 : 10 +0,5 : 0,7 ? |
д) 4,2+4,8 : 5 : 3 +4,4 ? |
ІІ варіант
|
а) 1,5+2 ·3 : 5 -1,1 ? |
б) 5.9-2 : 3 ·2 -1,6 ? |
в) 6-1,2 : 6 ·3 -0,4 ? |
г) 9 : 0,3 : 10 -1,2 :0,6 ? |
д)1,2+6,8 : 5 : 4 +4,6 ? |
Учні обмінюються листочками і здійснюють взаємоперевірку за записами на дошці (кожен приклад 2 бали).
Одержали відповіді: 1,1,2,3,5.
Результати записуються в оціночний листок.
Повідомлення
Якщо уважно розглянути отриманий ряд чисел і продовжити його за правилом: де кожне наступне число дорівнює сумі двох попередніх тоді утвориться ряд 1,1,2,3,5,8,13,21,34,... і т.д., який називається рядом Фібоначчі. Італійський математик Леонардо Пізанський (1180-1240) за прізвиськом Фібоначчі, що означає „син добродушного", гуляючи по лісу, звернув увагу на те, що, коли паросток ахілеї пробивається з-під землі, у нього виростає тільки один маленький листочок, потім на стеблі з'являється ще один, потім - два, а потім - три, а потім, число листків наростає у відповідності: 1,2,3,5,8,13,21,....
Таку ж саму закономірність він отримав, контролюючи кількість пелюсток у різних квітів. Так, лілії та іриси мають по 3 пелюсточки; лютики мають по 5 пелюсток; деякі дельфініуми - по 8; золотоцвіт - 13; у деяких айстр їх 21, у маргариток їх почти завжди 34, 55, або 89 пелюсток.
(Демонструються слайди)
В своїй „Книзі про рахунок" розв'язуючи, серед інших, задачу про те „скільки народиться кроликів за рік від однієї пари", Фібоначчі отримав ту ж саму послідовність чисел: 1,1,2,3,5,8,13,21,34...
Як показало життя ця послідовність постійно повторюється в оточуючому нас світі. І це ще не все. Цей ряд володіє дивною властивістю: якщо почати ділити одне число цієї послідовності на попереднє, ми будемо асимптотично наближатися до числа - 1,6180339.
Командна робота (три команди)
Учні заповнюють схеми заготовлені на дошці ( всі числа, записані в фігурах - невідомі).
І команда
51,9 ·8,4=
+0,0407=
:36=
· 0,01=
·10=
ІІ команда
31,18 ·4,5=
+0,1353=
·0,01=
:54=
·10=
ІІІ КОМАНДА
51,3 · 4,2=
+ 161,411=
: 54=
· 0,1=
: 100=
За кожен правильно розв'язаний приклад учні виставляють 1 бал в листок оцінювання.
Три команди отримали число 1,618, яке отримують в результаті «золотого перерізу».
Суть „золотої пропорції", або ще кажуть „золотого перерізу", заключається в наступному - менша частина цілого так відноситься до більшої, як більша частина до цілого. Іншими словами - під „золотим перерізом" розуміють поділ даного відрізка АВ точкою М так, щоб виконувалося співвідношення:
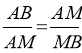
А__________х________М_______ _____В
Відношення більшого відрізка до меншого становить: 1,618 і це число відповідає „золотій пропорції".
Золота пропорція відповідає числу 1,6180339.
Вона виражає співрозмірність, гармонійність, красу природних об'єктів,
а також шедеврів мистецтва та архітектури.
III. РОЗВ'ЯЗУВАННЯ ВПРАВ
Диференційована робота з класом Група Б достає з конверта картки і працює самостійно.
РОЗВ'ЯЗАТИ ЗАДАЧУ (група б) (для самостійної роботи) . Висота всієї споруди Парфенона дорівнює 61,8 грецьким футам. Висота колони на 14,6 фута більша ніж висота перекриття й фронтону Знайти чому дорівнює відношення висоти колони до висоти перекриття й фронтону.(Відповідь округлити до тисячних)
Група А( розв'язує задачу на дошці)
Знайти відношення АС1/ С1D та АD/АС1 і порівняти їх. ( Отримали число 1,618.)
Група Б здає листочки вчителю.
Повідомлення
Якщо в коло вписати правильний п'ятикутник, одержимо пентаграму — геометричну фігуру, у якої кожна з п'яти діагоналей ділить іншу у відношенні „золотого перерізу". Піфагор вважав правильний п'ятикутник священним знаком і дарував його зображення тільки друзям, як символ дружби. Діагоналі ж п'ятикутника утворюють правильну зірку, яку піфагорійці сприймали, як символ здоров'я, радості, життя і добрих справ.
Композиція портрету Мони Лізи, відомого італійського художника Леонардо да Вінчі, який є шедевром світового мистецтва базується на „золотих трикутниках", що є частинами правильного зіркового п'ятикутника.
Група б повідомляє про результати своєї роботи (Одержали відношення 1,618)
Повідомлення
Вершиною давньогрецької архітектури вважається храм богині Афіни - Парфенон, побудований у V столітті до нашого літочислення. Храм має прямокутну основу. Вздовж периметра
збудована колонада. Колони, які здаються вертикальними, насправді трохи нахилені всередину. Завдяки цьому вони здаються стрункими й легкими.
„Золотим перерізом" Парфенон підкорює красою форм і закономірністю пропорцій. Відношення довжини цієї будівлі до її висоти відповідає „золотій пропорції" і становить 1,618.
«Золотим перерізом» керувалися стародавні єгипетські архітектори, що споруджували піраміду фараона Хеопса. В усіх внутрішніх і зовнішніх пропорціях піраміди число 1,618, грає центральну роль.
Славнозвісний Колізей теж будувався з дотриманням канонів краси. Споруди, які побудовані за правилами „золотої пропорції" завжди захоплюють нас своєю красою, своєю довершеністю.
Група А достає з конверта картки і працює самостійно.
І ВАРІАНТ (група А)
1. Знайти відношення А1С1:С1В і А1В: А1С1 і їх порівняти. Результат округлити до десятих.(8 балів )
2.Розв'язати рівняння 5х+2х-2,9=8,3 (+2бали)
II ВАРІАНТ (група А)
1. Знайти відношення АС:СВ і АВ:АС і їх порівняти. Результат округлити до десятих.(8 балів)
2.Розв'язати рівняння 5х +3х-4,9=7,9(+2бали)
Група Б (розв'язує задачу на дошці) Голова людини становить восьму частину всього тіла. В погрудді вмішується дві голови. Довжина від талії до
щиколоток дорівнює п'яти головам. Висота підйому ноги дорівнює 10 см
Знайти чому дорівнює кожна частина тіла людини, якщо зріст людини 186см.
(Всі величини перевести в метри.)
Група А здає листочки вчителю ( Учні роблять висновок, що річні витки спіралі мюшлі знаходяться у відношенні золотого перерізу).
Повідомлення
„Золотий переріз" зустрічається і на практиці мистецтва ваяння. Скульптори стверджують, що, якщо тіло досконале, то талія ділить його у відношенні „золотого перерізу", і це відношення дорівнює 1,168.
Каноном краси і довершеності вважається фігура
Статуї Аполона Бельведерського.
Для дорослого чоловіка відношення його зросту до лінії торсу становить 1,625
Статуя Давида, робота видатного італійського митця Мікеланджело, також вважається взірцем „золотої пропорції".
Для дорослих жінок відношення довжини тіла до довжини талії становить ~ 1,6
Група Б повідомляє про результати своєї роботи, та робить висновок, що перший і другий витки мушлі знаходяться у відношенні золотого перерізу.
(Учні які розв'язували задачі біля дошки роблять помітки в листку оцінювання.)
Повідомлення
Німецький фізик і психолог Густав Фехнер дослідив, що людині
Подобаються більше ті об'єкти, пропорції яких знаходяться у відношенні золотого перерізу. Виявляється, що кривизни акомо-дулюючого кришталика нашого ока відносяться як 3:5, що відповідає золотому перерізу. Тому нам більше подобаються і здаються прекрасними ті речі які відповідають золотому перерізу.
Повідомлення
Золота пропорція відома і в музиці. Так дослідження показали. Що в музичних творах визначних композиторів Баха, Бетховена, Моцарта та ін., кульмінація мелодії припадає на точку золотого перерізу, мелодія таких творів начебто розвивається, підкоряється законам математики, а саме закону золотого перерізу.
( Вчитель збирає листи оцінювання)
ІV . ЗВУЧИТЬ МУЗИКА.
УЧНІ РОЗВЯЗУЮТЬ КРОСВОРД.
|
|
1 |
|
Б |
|
|
|
|
||||||
|
|
2 |
е |
|
|
|
|
|||||||
|
3 |
|
т |
|
||||||||||
|
|
х 4 |
|
|
|
|
||||||||
|
о5 |
|
|
|
|
|||||||||
|
6 |
|
в |
|
|
|
|
|||||||
|
7 |
|
е |
|
|
|
|
|
|
|
||||
|
8 |
|
|
|
|
|
н |
|
|
|
||||
- Результат множення двох чисел.
- Розрядна одиниця.
- Фігура, яка складається з двох променів, що мають спільний початок.
- Відрізок, який з'єднує дві точки кола.
- Найменше натуральне число.
- Найбільше одноцифрове число.
- Властивість додавання.
- Фігура, яка складається з трьох точок і трьох відрізків, що попарно з'єднують ці точки.
- ПІДСУМОК УРОКУ.
- ЗАКЛЮЧНЕ СЛОВО ВЧИТЕЛЯ.
Сьогодні на уроці ви познайомились із застосуванням золотого перерізу. Як ви бачите математика присутня в усьому: вона і в устрої рослини, вона і в тілі людини, вона і в музиці, і за її законами будується всесвіт. Математика – це не тільки сухі формули, теореми та їх доведення, а це ще й краса. Ви бачите, як тісно, майже нерозривно пов’язані математика і закони прекрасного, що закони краси мають математичний характер.
А наша зустріч підійшла до завершення і мені хочеться нагадати слова
М. В. Ломоносова “ Математику тому вивчати слід, що вона розум до ладу приводить.”
1
про публікацію авторської розробки
Додати розробку