Урок "Пропорція. Основна властивість пропорції."
Міністерство освіти і науки України
Новгород-Сіверська державна гімназія імені К.Д. Ушинського
Відкритий урок
«Пропорція. Основна властивість пропорції»
Підготувала :
вчитель математики Тимохович Анна Вікторівна
2015 н.р.
Тема. Пропорція. Основна властивість пропорції (слайд 1).
Мета. Формувати поняття «пропорції», «крайніх і середніх членівпропорції», виконувати вправи, що передбачають знаходження невідомого члена пропорції, застосовувати пропорції до розв’язування задач.
Розвивати логічне мислення, пізнавальний інтерес, культуру математичного мовлення, пам’ять, уяву.
Виховувати самостійність, наполегливість і старанність у роботі, дисциплінованість, впевненість у своїх знаннях, взаємоповагу.
Тип уроку: засвоєння нових знань, формування вмінь.
Матеріали і обладнання: мультимедійна дошка, комп’ютерна презентація, картки із завданнями.
План уроку(слайд2)
- Перевірка домашнього завдання.
- Актуалізація опорних знань.
- Означення пропорції. Крайні і середні члени пропорції.
- Основна властивість пропорції.
- Знаходження невідомого члена пропорції.
- Розв’язування вправ і задач.
- Домашнє завдання.
Тема і план уроку представлені на слайдах 1 і 2.
- Перевірка домашнього завдання.
Наявність письмової домашньої роботи заздалегідь перевіряють учні-консультанти. Вони також коментують недоліки виконання вправ деяких учнів.
- Актуалізація опорних знань (відбувається у формі фронтальної бесіди):
- Що таке відношення (слайд 3)?
Кожному питанню актуалізації присвячено окремий слайд: спочатку на екрані з’являється запитання до класу, після його обговорення – правильна відповідь.
Означення відношення (слайд 4).
(Частку від ділення одного числа на друге називають відношенням цих чисел.)
- Сформулюйте основну властивість відношення (слайд 5).
Основна властивість відношення (слайд 6).
(Відношення двох чисел не зміниться, якщо кожне з них помножити або поділити на одне й те саме число, відмінне від нуля.)
- Сформулюйте наслідки, які випливають з основної властивості відношення (слайд 7).
Наслідки основної властивості відношення (слайд 8).
(Обидва члени відношення можна поділити на їх спільний дільник.Відношення дробових чисел можна замінити відношенням натуральних чисел.)
ІІІ.Сприйняття та первинне усвідомлення нового матеріалу.
- Означення пропорції. Крайні і середні члени пропорції.
Відношення ![]() і
і ![]() рівні між собою:
рівні між собою: ![]() =
= ![]() , 1:2=3:6.
, 1:2=3:6.
Такі рівності називають пропорціями (слайд 9).
У пропорції a:b=c:d - a іd називають крайніми членами, а bіc – середніми членами пропорції.
- Основна властивість пропорції.
«Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати». (Д. Пойа)
«…Діти не повинні виучувати ніякі арифметичні правила, а самі відкривати їх».( К. Д. Ушинський) (слайд 10)
Робота в парах
(Учні об’єднуються в пари. Кожна пара самостійно розв’язує запропоноване завдання. Хто перший виконав – піднімає сигнальну картку).
Знайдіть добуток середніх і крайніх членів пропорції (слайд 11):
-
0,3 : 8 = 6 : 160; 2)
 :
: = 6 : 9; 3) 0,6 : 0,15 = 20 : 5.
= 6 : 9; 3) 0,6 : 0,15 = 20 : 5.
Учні усно дають відповіді, формулюють правила і записують властивість пропорції на дошці в буквеному вигляді (слайд 12).
(Добуток крайніх членів кожної пропорції дорівнює добутку її середніх членів. Якщо а:b=с:d, то а·d= b·с.)
Пропонується доведення основної властивості пропорції (слайд 13).
(Нехай дано довільну пропорцію ![]() =
=![]() . Помноживши обидві частини цієї рівності на добуток b·d,матимемо
. Помноживши обидві частини цієї рівності на добуток b·d,матимемо ![]() =
=![]() . Скоротивши перший дріб на b, а другий – на d, дістанемо рівність а·d= с·b. Отже, якщоа:b=с:d, то а·d= b·с.)
. Скоротивши перший дріб на b, а другий – на d, дістанемо рівність а·d= с·b. Отже, якщоа:b=с:d, то а·d= b·с.)
- Знаходження невідомого члена пропорції (слайд 14):
х:2=10:5,
х∙5=2∙10,
х=20:5,
х=4.
Правило знаходження невідомого члена пропорції.
(Щоб знайти невідомий крайній член пропорції, досить добуток її середніх членів поділити на відомий крайній. Щоб знайти невідомий середній член пропорції, досить добуток її крайніх членів поділити на відомий середній.)
Приклади виконання вправи і розв’язування рівнянь (слайд 15):
1. Складання пропорцій з чисел 3, 4, 8 і 6:
4:3=8:6; 4:8=3:6; 8:4=6:3; 3:4=6:8.
2. Приклади розв’язування рівнянь:
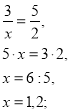

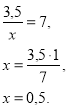
IV.Формування вмінь
Наведені вправи спрямовані на засвоєння основної властивості пропорції, але для їх виконання застосовуються дії із звичайними і десятковими дробами, що були вивчені раніше. Це сприяє застосовувати набуті знання в різних ситуаціях.
Кількість вправ та їх складність, форми і методи подачі матеріалу вчитель визначає залежно від рівня підготовки учнів.
Виконання усних вправ ( слайд 16):
- Чи вірні відношення:
- 9 : 4,5 і 21 : 10,5 ; 2)6 : 18 і 8 : 24?
- Замініть відношення дробових чисел відношенням натуральних чисел:
-
1 :
 ; 2)
; 2)  : 2; 3)
: 2; 3) 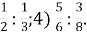
- Відношення чисел 3 і 4 дорівнює відношенню чисел:
1) 3 і 10; 2) 1 і 4; 3) 9 і 12; 4) 6 і 12.
Виконання усних вправ (слайд 17):
- Прочитайте пропорцію, назвіть її крайні та середні члени:
-
48 : 8 = 36 : 6; 2)12 : 5 = 48 : 20; 3)
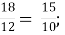 4)
4) 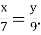
- Який із записів є істинною пропорцією:
а) 1 :6 = 2: 3; б) 1 : 2 = 6 : 3; в) 1 : 3 = 6 : 2; г) 1 : 3 = 2 : 6?
6. Як знай ти невідомий член пропорції:
1) х : 10 = 4 : 5; 2) 7: х = 35 : 20?
Виконання письмових вправ ( слайд 18):
- Використовуючи числа 63; 72; 8; 7, складіть пропорцію.
- Складіть 6 пропорцій, використавши рівність 2 ∙ 9 = 3 ∙ 6.
- Знайдіть невідомий член пропорції ( слайд 19):
- х : 6 = 12:8; 2) х : 10 = 15 : 25;
3) 0,2 : 3 = х : 5; 4) х : 7 = 3 : 10,5;
5) х : ![]() 6) 3
6) 3 ![]()
7) ![]() 8)
8) ![]()
Відповіді (слайд 20): 1) 9; 2) 6; 3) ![]() 4) 2; 5)
4) 2; 5) ![]() 6) 2; 7) 6; 8) 33
6) 2; 7) 6; 8) 33![]()
- Розв’яжіть рівняння (слайд 21):
-
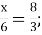 2)
2) 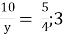 )
) 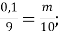 4)
4) 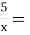 1,3; 5)
1,3; 5) 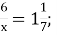 6) 2
6) 2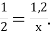
Відповіді (слайд 22): 1) 16; 2) 8; 3)![]() 4) 4
4) 4![]() 5) 5
5) 5![]() ; 6)
; 6) ![]()
Розв’яжіть рівняння (слайд 23):
-
2,5 : 2
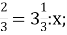 2) 3
2) 3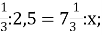 3) 6
3) 6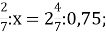
4) 2![]() 5) 4
5) 4![]() 6) 5
6) 5![]()
Відповіді (слайд 24): 1) 3![]() 2)5,5; 3) 1
2)5,5; 3) 1![]() 4) 12; 5) 2
4) 12; 5) 2![]() 6) 2
6) 2![]()
Розв’яжіть рівняння ( слайд 25):
-
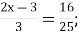 2)
2) 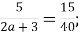 3)
3) 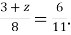
Відповіді ( слайд 26): 1) 2![]() 2)5
2)5 ![]() 3) 1
3) 1![]()
Замовлення вчителя географії (слайд 27):
- Відстань на карті між двома пунктами на карті становить 4,3 см. Яка відстань між цими пунктами на місцевості, якщо карта має масштаб 1:1000 000?
- Відстань між двома пунктами на місцевості дорівнює 340 км. Яка відстань між цими пунктами на карті, якщо її масштаб дорівнює 1 : 2000 000?
- Відстань між двома пунктами на місцевості дорівнює 405 км, а на карті – 5,4 см. Знайдіть масштаб карти.
Відповіді ( слайд 28): 1. 43 км; 2. 17 см; 3. 1:7500000.
- Підсумок уроку
Бліц-тест (слайд 29):
Варіант1 Варіант2
Розв’яжіть рівняння: Розв’яжіть рівняння:
a)![]() б) 5:7=х:91; а)
б) 5:7=х:91; а) ![]() б) 12:х =15 : 5;
б) 12:х =15 : 5;
в) ![]() г)
г)![]() в)
в) ![]() г)
г)![]() .
.
Відповіді (слайд 30): Варіант 1: а) 4; б) 65; в) 10; г) 2![]()
Варіант 2: а)16; б) 4; в) ![]() г) 7.
г) 7.
Рефлексія (слайд 31):
Запитання до учнів: « Як би ти оцінив свої здобутки на уроці?»
Пропонується підняти картки із зображеннями, які означають наступне.
![]() - « Я все зрозумів, тест показав, що я все роблю правильно».
- « Я все зрозумів, тест показав, що я все роблю правильно».
![]()
![]() - « Мені була зрозуміла більша частина матеріалу, але я ще іноді припускаюся помилок».
- « Мені була зрозуміла більша частина матеріалу, але я ще іноді припускаюся помилок».
![]() -« Я майже нічого не розумію, нове правило для мене дуже складне».
-« Я майже нічого не розумію, нове правило для мене дуже складне».
VI.Домашнє завдання.
Учитель обирає домашнє завдання залежно від результатів рефлексії. Один із варіантів – учням, які не дуже добре зрозуміли навчальний матеріал на уроці, дати додому картки – підказки,що допоможуть їм впоратись із домашнім завданням.
За підручником (Бевз Г. П., Бевз В. Г. Математика: Підруч. для 6 кл. загальноосвіт. навч. закл. – К.:Генеза,2006):
опрацювати §19, №673 – рівень А, № 677 – рівень Б, ст. 131(cлайд 32).
Література
- Бевз Г. П., Бевз В. Г. Математика:Підруч. для 6 кл. загальноосвіт. навч. закл. – К.:Генеза, 2006.
- Капіносов А. Дидактичні матеріали для тематичних атестацій з математики. 6 клас. – Т.:Підручники і посібники, 2001.
- Мерзляк А. Г., Полонський В. Б., Рабінович Ю. М., Якір М. С. Математика 6 клас: Збірник задач і завдань для тематичного оцінювання.- Х: Гімназія, 2007.
- Мерзляк А. Г., Полонський В. П., Якір М. С. Математика 6 клас: Книга для вчителя.- Х.: Гімназія, 2008.
- Румен Л. На допомогу вчителю: Математика. Шкільний світ. - № 46-47 (490-491), 2008.
- Програмно-методичний комплекс навчального призначення для загальноосвітніх закладів. Математика 6 клас. Уроки 41,44.
Додаток 1
Дізнайтеся більше
Якщо пропорція а:b = c : d правильна, то правильна і рівність ad = bc. Поділивши обидві її частини на cd, матимемо ![]() звідси
звідси ![]() або a:c=b:d.
або a:c=b:d.
Отже, середні члени пропорції можна міняти місцями.
Так само можна показати, що міняти місцями можна і крайні члени пропорції.
Наприклад, оскільки 0,2:0,3=2:3, то правильні також пропорції 0,2:2=0,3:3 і 3:0,3 = 2:0,2.
![]()
|
|
![]()
|
|
|
|
|
|
|
|
Додаток 2
Програмно-методичний комплекс навчального призначення для загальноосвітніх закладів. Математика 6 клас. Уроки 41,44.
1


про публікацію авторської розробки
Додати розробку
