Урок "Прості і складені відсотки"

УРОК № 41

Тема. Відсоткові розрахунки. Формула складних відсотків

 

Мета уроку:

 домогтися засвоєння учнями змісту: означення поняття «складні відсотки»;

 формули складних відсотків.

 

 Систематизувати знання учнів:

про означення поняття «відсоток від числа»;

формули, що виражають способи розв'язування основних задач на відсотки.

 

Виробити вміння:

відтворювати зміст вивчених понять та алгоритмів і застосовувати їх для розв'язування вправ, що передбачають розв'язування основних задач на відсотки, а також застосування формули складних (банківських) відсотків.

Тип уроку: засвоєння знань, вироблення вмінь.

Наочність та обладнання:  опорний конспект , підручник «Алгебра 9 клас» Істер.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

III. Формулювання мети і завдань уроку.

IV. Актуалізація опорних знань та вмінь учнів

Усні вправи

1.   Виконайте множення:

1) 0,5 · 48;  2) 0,2 · 60;    3) 1,5 · 20;    4) 0,1 · 17.

2.   Знайдіть:

1)  від 15;

2) 0,3 від 3;

3) число, якщо  від нього дорівнює 4,9;

4) яку частину становить число 5 від числа 25.

 

3.   Знайдіть значення виразу 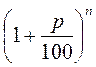, якщо:

1) р = 10; n = 2;         

2) р = 50; n = 3.

4.   Знайдіть значення виразу 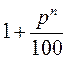, якщо:

1) р = 10; n = 2;         

2) р = 20; n = 6.

V. Систематизація знань. Формування нових знань

Серед прикладних задач, які можуть бути розв'язані методом математичного моделювання, значне місце посідають задачі, у яких мова йде про відсотки, тому сьогодні на уроці ми поговоримо про гроші і як за допомогою них можна збільшити свій капітал.

Давайте уявимо , що ви отримали у спадок 50000 гривень. Ваші дії?

Все це добре, але щоб примножити свої гроші потрібно щоб вони «працювали». А це можливо коли їх положити в банк на депозит.

Отже, ми відкрили у банку депозит у розмірі 50000 грн під 11% річних від початкової суми вкладу.

Як знайти 11% від 50000?  Так 50000∙0,11=5500грн – відсоткові кошти за 1 рік, за 2 роки 5500∙2=11000 грн. , за 3 роки - 5500∙3=16500 грн.

Нарощений капітал = початкова сума+відсотки=50000+5500=55500 грн.

За 3 роки на простих відсотках 50000+16500=66500 грн

Формулами можна записати так ,

А₀ – початковий капітал (50000 грн)

Р% - відсоток річних (11%)

А₁ – нарощений капітал

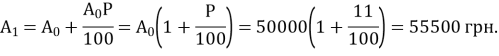
Це при умові що ви будете знімати кожний рік відсоткові кошти або у вас в угоді буде обумовлено, що відсоток нараховуватиметься на початкову суму.

А якщо ми відсотки не будемо знімати і річні відсотки нараховуватимуться на нову суму то ми отримаємо:

Нарощений капітал за 1 рік – 55500 грн

Нарощений капітал за 2 рік –

Нарощений капітал за 3 рік -

Але ці обрахунки за кожний рік можна не робити, а використати формулу складних відсотків     ,

А_n – нарощений капітал через n років,

А₀ – початковий капітал,

р% - відсоткова щорічна ставка 

Давайте перевіримо чи виконується наша формула під наш депозит:

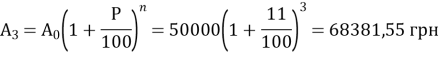
Отже, якщо депозит положити на один рік або знімати кожного року відсоток то обчислюється за формулою простих відсотків , а якщо ми положимо на 2 і більше років і не зніматимемо відсотки то обраховуватимемо за формулою складних відсотків .

Скажіть, що спільного і що відмінного між цими формулами?

Ми положили  50000 грн.  в банк  двома способами

І спосіб . Відсоток рахувався на початкову суму і в загальному ми отримали за 3 роки – 66500 грн.

ІІ спосіб. Відсоток нараховували від суми яка була на початок кожного року і ми отримали 68381,55 грн.

Скажіть мені, будь ласка, що потрібно простежити при підписанні угоди з банком?

VI. Формування вмінь. 

Письмові вправи. Робота з підручником.

№ 801

А₀=10000 грн.       р=11%

1. 
2. (округлюємо до сотих)

Щоб отримати відсоткові гроші потрібно від нарощеного капіталу(А_n ) відняти початковий капітал (А₀)

А₃ – А₀ = 13676,31 – 10000 = 3676,31 грн.

А₅ – А₀=16850,58 – 10000 = 6850,58 грн.

№ 802, №806.

Де в житті ми використовуємо формули простих і складних відсотків?

VII. Підсумки уроку

Контрольне завдання

Нехай початковий внесок дорівнює а грн; річна відсоткова ставка b%. Скільки грошей буде на рахунку вкладника через с років?

1) а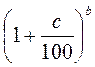;       2) b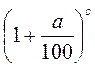;    3) а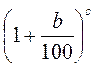;     4) с.

 

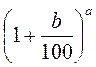VIII. Домашнє завдання

1.   Повторити означення відсотків і вивчити формули розв'язування задач на відсотки та формулу складних відсотків.

2.   Розв'язати задачі №802, №806